并行分布式计算 并行计算性能评测
文章目录
- 并行分布式计算 并行计算性能评测
- 基本性能指标
- 参数
- CPU 基本性能指标
- 存储器性能
- 并行与存储开销
- 加速比性能定律
- Amdahl 定律
- Gustafson 定律
- Sun 和 Ni 定律
- 加速比讨论
- 可括放性评测标准
- 等效率度量标准
- 等速度度量标准
- 平均延迟度量标准
- 基准评测程序(Benchmark)
并行分布式计算 并行计算性能评测
基本性能指标
参数
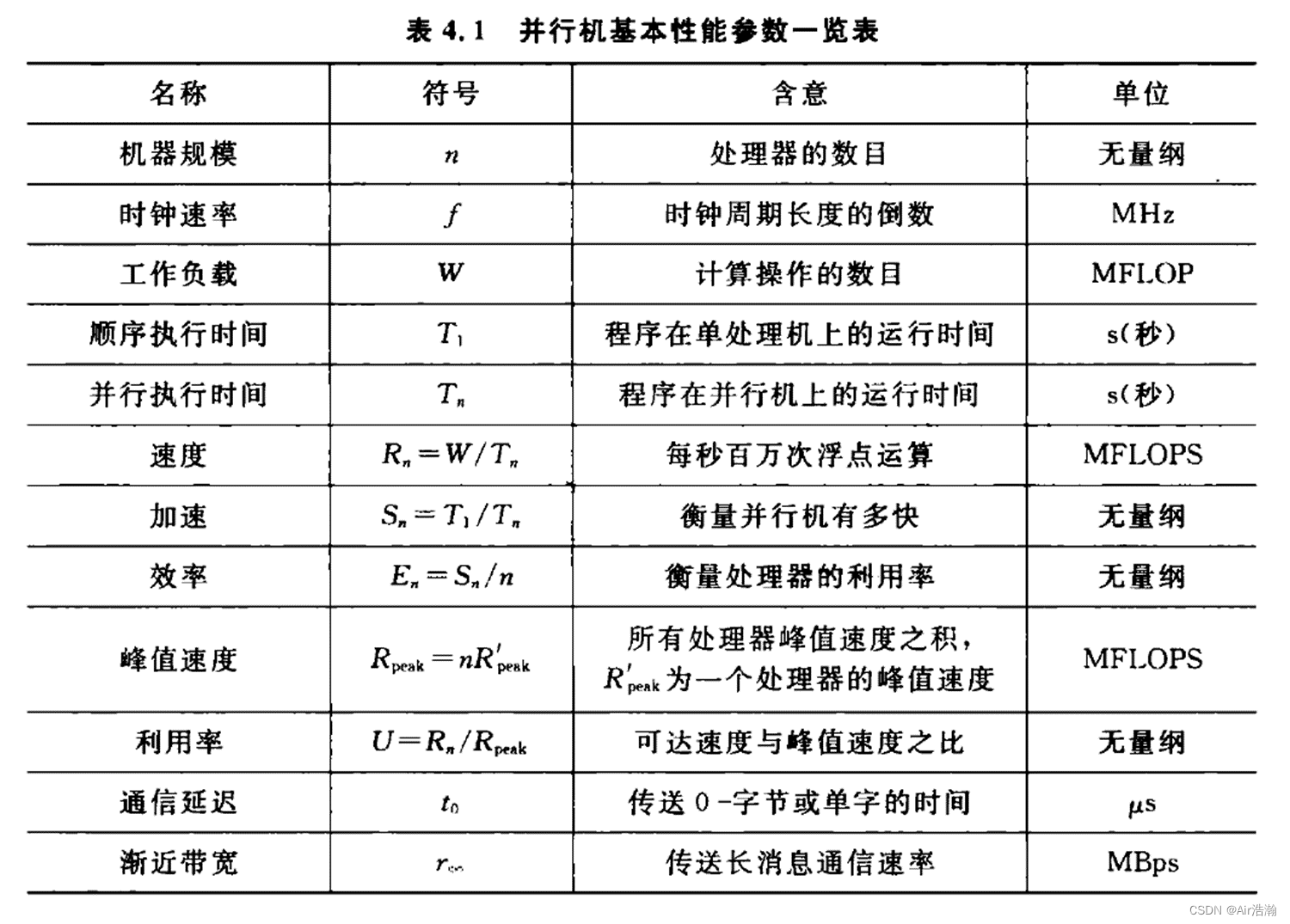
- 工作负载 W:是指某个算法的计算量;
- 加速:就是加速比;
- 峰值速度:是速度的理论上限;
CPU 基本性能指标
① 工作负载:
- 执行时间:不仅包括 CPU 时间,还包括访问存储器、磁盘时间、 I/O 时间和 OS 开销等;执行时间是不稳定的,波动较大;
- 浮点运算数(Flops):其他类型的运算可以通过经验折算成浮点运算速度;只能衡量计算任务,不能用于衡量数据传输、IO密集型的操作(虽然并行计算前期只是用于计算密集型的任务)
- 指令数目(MIPS)通常以 百万条/秒 作为单位(单条指令的执行时间差别很大)
② 无重叠的假定下并行执行时间 T n T_n Tn :
- 计算时间 T c o m p u t T_{comput} Tcomput ;并行开销时间 T p a r o T_{paro} Tparo ;相互通信时间 T c o m m T_{comm} Tcomm :
T n = T c o m p u t + T p a r o + T c o m m T_n=T_{comput}+T_{paro}+T_{comm} Tn=Tcomput+Tparo+Tcomm
- T c o m p u t T_{comput} Tcomput :与串行的时间是一致的(无重叠的假定);
- T p a r o T_{paro} Tparo :与进程管理、组操作、进程查询等相关;
- T c o m m T_{comm} Tcomm :同步(路障、锁、临界区、事件)、通信、聚合操作(规约、前缀运算),一般来说 T c o m m T_{comm} Tcomm 比 T p a r o T_{paro} Tparo 要大得多;
存储器性能
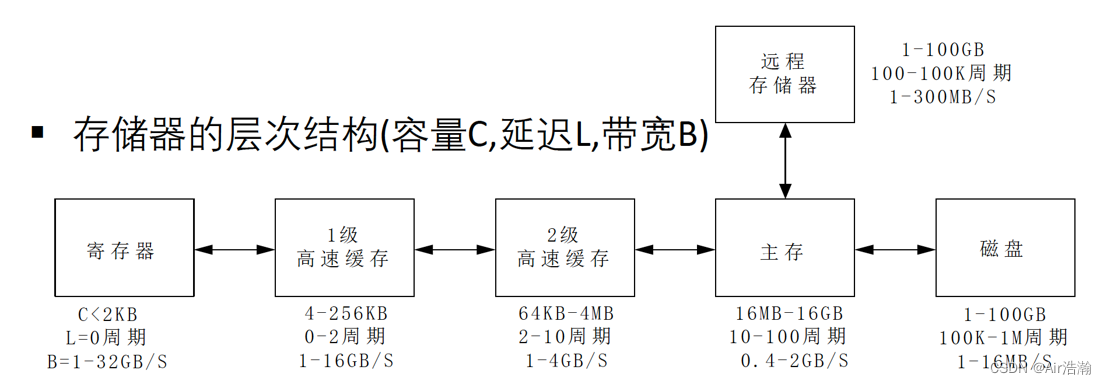
估计存储器的带宽:例如 RISC 的加法可以在单拍内完成(取出两个数相加再送回寄存器);假定字长为 8B,时钟频率 100MHZ,则带宽:
B = 3 × 8 × 100 × 1 0 6 B / s = 2.4 G B / s B=3\times8\times100\times10^6 B/s=2.4GB/s B=3×8×100×106B/s=2.4GB/s
并行与存储开销
并行和通信的开销相对于计算来说很大。
开销的测量:
- 乒乓方法(Ping-Pong Scheme):节点 - 发送 m 个字节给节点 1,节点 1 收到以后立即将消息发回节点 0,总时间除以 2;
- 热土豆法(Hot-Potato)/救火队法(Fire-Brigade):再乒乓方法的基础上,节点 1 收到以后立即发送给节点 2,直到发送给节点 n-1 后,最后发送回 0,总的时间除以 n;
点到点通信开销表达式:
t ( m ) = t 0 + m / r ∞ t(m)=t_0+m/r_{\infty} t(m)=t0+m/r∞
-
m m m :消息长度(字节数);
-
t 0 t_0 t0 :通信启动时间;
-
r ∞ r_{\infty} r∞ :渐进带宽,传送无限长消息时的通信频率;查利芳等网络结构就是为了增大渐进带宽;
-
半峰值长度 m 1 2 m_{\frac{1}{2}} m21 :达到一半渐进带宽所需要的消息长度;
-
特定性能 π 0 \pi_0 π0 :表示短消息带宽;
-
t 0 = m 1 2 / r ∞ = 1 / π 0 t_0=m_{\frac{1}{2}}/r_{\infty}=1/\pi_0 t0=m21/r∞=1/π0 ; t 0 t_0 t0 就好像是发送一个很小的包时所需要花费的时间;
典型整体通信:
- 广播(Broadcasting):处理器 0 发送 m 个字节给所有的 n 个处理器;
- 收集(Gather):处理器 0 接收所有 n 个处理器发送来的消息,最终接收 mn 个字节;尽量不要出现收集的情况,否则带宽会被 n 个处理器瓜分;
- 散射(Scatter):处理器 0 发送了 m 个字节的不同消息给所有 n 个处理器;
- 全交换(Total Exchange):每个处理器均彼此相互发送 m 个字节的不同消息给对方,总通信量为 m n 2 mn^2 mn2 个字节;很多算法需要全交换,所以通行效率或者带宽会随着处理器数量上升而快速下降;
- 循环位移(Circular-shift):处理器 i 发送 m 个字节给处理器 (i + 1) % n,总通信量为 mn 个字节;
机器的成本与价格:
- 机器的性价比(Performance/Cost Ratio):单位代价(通常为百万美元)所获取的性能(通常用 MIPS 或 MFLOPS 表示)
- 利用率:可达到的速度与峰值速度之比;
要想提高利用率,就要提高通讯量级;要想保持通讯硬件不变而提高通讯量级,就要优化算法。
加速比性能定律
Amdahl 定律
前提:
- 固定不变的计算机负载;
- 固定的计算负载分布在多个处理器上;
- 增加处理器加快执行速度,从而达到了加快处理速度的目的;
(总的计算量不变,并且被固定地、平均地分配给 p 个处理器)
参数:
-
P P P:处理器数;
-
W W W:问题规模(计算负载、问题的总计算量)
W = W s + W p W=W_s+W_p W=Ws+Wp- W s W_s Ws :应用程序中的串行分量, f f f 是串行分量比例( f = W s / W f=W_s/W f=Ws/W);
- W p W_p Wp :应用程序中可并行化部分;
-
T s = T 1 T_s=T_1 Ts=T1 :串行执行时间;
-
T p T_p Tp :并行执行时间;
-
S S S :加速比;
-
E E E :效率;
S = W s + W p W s + W p / p → p → ∞ 1 f S=\frac{W_s+W_p}{W_s+W_p/p} \stackrel{p\to\infty}{\to} \frac{1}{f} S=Ws+Wp/pWs+Wp→p→∞f1
特点:
-
适用于实时应用问题。当问题的计算负载或者规模固定时,必须通过增加处理器数目来降低计算时间;
-
加速比受到算法中串行工作量的限制;
-
扩展:若并行实现时还有额外开销,则:
S = W s + W p W s + W p / p + W o → p → ∞ 1 f + W o / W S=\frac{W_s+W_p}{W_s+W_p/p+W_o} \stackrel{p\to\infty}{\to} \frac{1}{f+W_o/W} S=Ws+Wp/p+WoWs+Wp→p→∞f+Wo/W1
Gustafson 定律
前提:对于很多大型计算,精度要求很高,而计算时间时固定不变的。此时为了提高精度,必须加大计算量,相应地必须增多处理器数才能维持时间不变。
(增大精度的同时 W s W_s Ws 几乎是不变的)
S ′ = W s + p W p W s + p W p / p = W s + p W p W s + W p = f + p ( 1 − f ) S'=\frac{W_s+pW_p}{W_s+pW_p/p}=\frac{W_s+pW_p}{W_s+W_p}={f+p(1-f)} S′=Ws+pWp/pWs+pWp=Ws+WpWs+pWp=f+p(1−f)
考虑并行开销 W o W_o Wo :
S ′ = W s + p W p W s + p W p / p + W o = f + p ( 1 − f ) 1 + W o / W S'=\frac{W_s+pW_p}{W_s+pW_p/p+W_o}= \frac{f+p(1-f)}{1+W_o/W} S′=Ws+pWp/p+WoWs+pWp=1+Wo/Wf+p(1−f)
特点:随着处理器数目的增加,串行执行部分 f f f 不再是并行算法的瓶颈。
Sun 和 Ni 定律
前提:充分利用存储空间等计算资源,尽量增大问题规模以产生更好/更精确的解,是 Amdahl 定律和 Gustafson 定律的推广。
推导:设单机存储容量为 M M M ,其工作负载 W = f W + ( 1 − f ) W W=fW+(1-f)W W=fW+(1−f)W ;
当并行系统有 p p p 个节点时,存储容量变为 p M pM pM ,用 G ( p ) G(p) G(p) 表示系统的存储容量增大 p p p 倍时工作负载的增加量,即存储容量扩大后的工作负载为 W = f W + ( 1 − f ) G ( p ) W W=fW+(1-f)G(p)W W=fW+(1−f)G(p)W ,加速比为:
S ′ ′ = f W + ( 1 − f ) G ( p ) W f W + ( 1 − f ) G ( p ) W / p = f + ( 1 − f ) G ( p ) f + ( 1 − f ) G ( p ) / p S''=\frac{fW+(1-f)G(p)W}{fW+(1-f)G(p)W/p}=\frac{f+(1-f)G(p)}{f+(1-f)G(p)/p} S′′=fW+(1−f)G(p)W/pfW+(1−f)G(p)W=f+(1−f)G(p)/pf+(1−f)G(p)
考虑并行计算的开销 W o W_o Wo :
S ′ ′ = f W + ( 1 − f ) G ( p ) W f W + ( 1 − f ) G ( p ) W / p + W o = f + ( 1 − f ) G ( p ) f + ( 1 − f ) G ( p ) / p + W o / W S''=\frac{fW+(1-f)G(p)W}{fW+(1-f)G(p)W/p+W_o}=\frac{f+(1-f)G(p)}{f+(1-f)G(p)/p+W_o/W} S′′=fW+(1−f)G(p)W/p+WofW+(1−f)G(p)W=f+(1−f)G(p)/p+Wo/Wf+(1−f)G(p)
- 当 G ( p ) = 1 G(p)=1 G(p)=1 时,就是 Amdahl 定律,意味着节点的扩展不会带来额外开销;
- 当 G ( p ) = p G(p)=p G(p)=p 时,就是 Gustafson 定律;
- 当 G ( p ) > p G(p)>p G(p)>p 时,加速比比前面两个定律得到的加速比更大;
加速比讨论
加速比经验公式:
p log p ≤ S ≤ p \frac{p}{\log p}\leq S \leq p logpp≤S≤p
-
线性加速比:很少通信开销的矩阵相加、内积运算等;
-
p / log p p/\log p p/logp 的加速比:分治类的应用问题;
-
通信密集类的应用问题: S = 1 C ( p ) S=\frac{1}{C(p)} S=C(p)1 ,这里 C ( p ) C(p) C(p) 时 p p p 个处理器的某一通信函数;
超线性加速:特殊情况下出现,例如在不同分支上进行搜索,某个处理器搜索发现结果后结束整个任务;
绝对加速:最佳串行算法与并行算法所用时间之比;(有些算法是没法直接并行化的,因此绝对加速更合理)
相对加速:同一算法在单机和并行机的运行时间。
可括放性评测标准
可括放性(Scalability):性能随处理器数的增加而按比例提高的能力。
- 影响因素:处理器数和问题规模;串行分量;并行处理的额外开销;处理器数是否超过了算法中的并发程度;
- 增加问题规模的好处:提供较高的并发机会;overhead 增加可能慢于有效计算的增加;串行分量比例随着问题规模增大而缩小;
- 增加处理器数量会增大 overhead 并降低处理器利用率,对于一个特定的并行系统(算法或程序),它们能否有效利用不断增加的处理器的能力应是受限的,而度量这种能力就是可括放性这一指标。
等效率度量标准
参数:令 t e i t^i_e tei 和 t o i t^i_o toi 分别是并行系统上第 i i i 个处理器的有用计算时间和额外开销时间(包括通信、同步和空闲的等待时间等)
T s = T e = ∑ i = 0 p − 1 t e i T 0 = ∑ i = 0 p − 1 t o i T_s=T_e=\sum\limits_{i=0}^{p-1}t_e^i \quad\quad T_0=\sum\limits_{i=0}^{p-1}t_o^i Ts=Te=i=0∑p−1teiT0=i=0∑p−1toi
T p T_p Tp 是 p p p 个处理器系统上并行算法的运行时间,对于任意 i i i 显然有:
T p = t e i + t o i p T p = T e + T o T_p=t^i_e+t_o^i \quad\quad pT_p=T_e+T_o Tp=tei+toipTp=Te+To
问题的规模 W W W 定义为最佳串行算法所完成的计算量,则 W = T e W=T_e W=Te ,因此有:
S = T e T p = T e ( T e + T o ) / p = p 1 + T o / W E = S p = 1 1 + T o / W S=\frac{T_e}{T_p}=\frac{T_e}{(T_e+T_o)/p}=\frac{p}{1+T_o/W}\quad\quad E=\frac{S}{p}=\frac{1}{1+T_o/W} S=TpTe=(Te+To)/pTe=1+To/WpE=pS=1+To/W1
为了维持一定的效率,处理器数 p p p 增大时,开销 T o T_o To 增大,问题规模 W W W 也需要相应增大。由此定义函数 f E ( p ) fE(p) fE(p) 为问题规模 W W W 随处理器数 p p p 变化的函数,为等效率函数。
优点:简单可定量计算的、少量参数计算等效率函数
缺点:如果 T o T_o To 无法计算出的话就不能用这个方法(比如在共享存储并行机中)
如图,3 到 1 可括放性越来越好,2 以上的表示不可扩放:
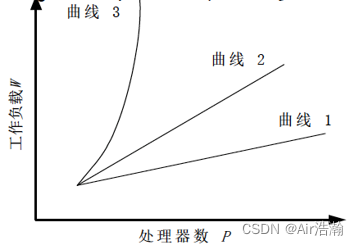
等速度度量标准
前提:在共享存储并行机中 T o T_o To 难以计算;换一种方法,如果速度能以处理器数的增加而线性增加,则说明系统具有很好的扩放性。
参数: p p p 和 W W W 前面一样, T T T 为并行执行时间,并行计算的速度 v = W / T v=W/T v=W/T ;
p p p 个处理器的并行系统的平均速度定义为并行速度除以处理器个数:
v ˉ = v p = W p T \bar{v}=\frac{v}{p}=\frac{W}{pT} vˉ=pv=pTW
令 W ′ W' W′ 表示当处理器数从 p p p 增大到 p ′ p' p′ 时,为了保持整个系统的平均速度不变所需执行的工作量,则可得到处理器数从 p p p 到 p ′ p' p′ 时平均速度可扩放度量标准公式:
Ψ ( p , p ′ ) = p ′ W p W ′ \Psi(p,\,p')=\frac{p'W}{pW'} Ψ(p,p′)=pW′p′W
Ψ ( p , p ′ ) \Psi(p,\,p') Ψ(p,p′) 介于 0 到 1 之间,越靠近 1 越好;
优点:直观使用易测量的机器性能速度指标来度量;
缺点:某些非浮点运算可能造成性能的变化没有考虑;
当 p = 1 p=1 p=1 时,有:
Ψ ( p ′ ) = Ψ ( 1 , p ′ ) = p ′ W W ′ = T 1 T p ′ = 解决工作量为 W 的问题所需串行时间 解决工作量为 W ′ 的问题所需并行时间 \Psi(p')=\Psi(1,\,p')=\frac{p'W}{W'}=\frac{T_1}{T_{p'}}=\frac{\text{解决工作量为$W$的问题所需串行时间}}{\text{解决工作量为$W'$的问题所需并行时间}} Ψ(p′)=Ψ(1,p′)=W′p′W=Tp′T1=解决工作量为W′的问题所需并行时间解决工作量为W的问题所需串行时间
区别:
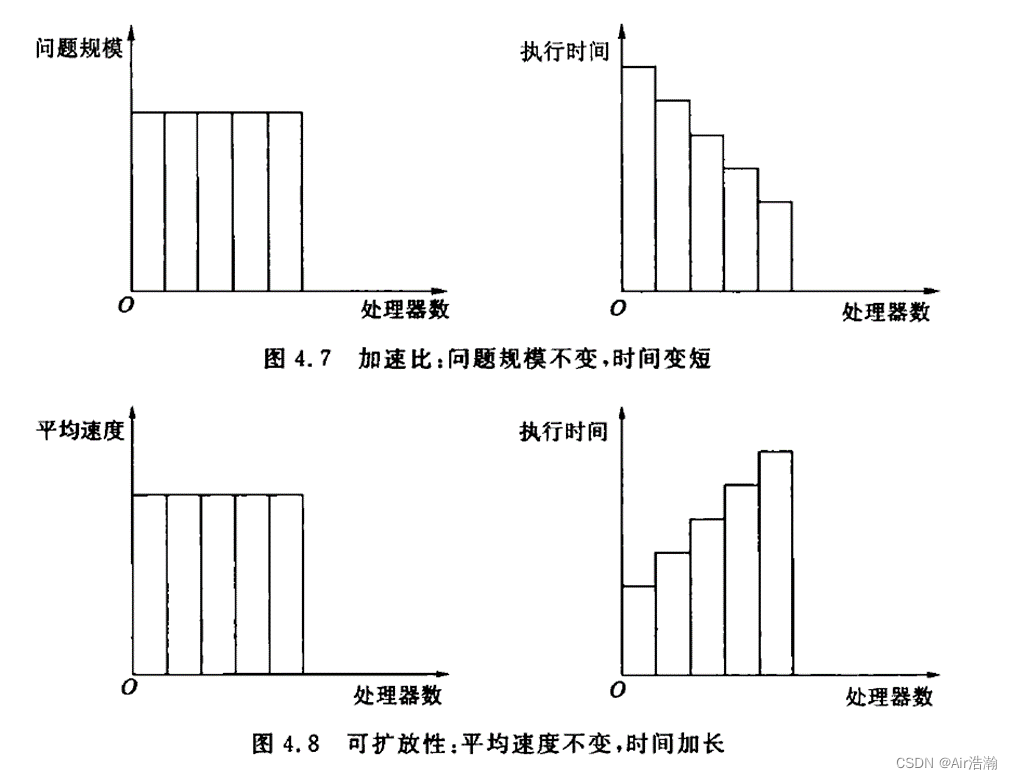
- 加速比的定义是保持问题规模不变,标志对于串行系统的性能增加;
- 扩放性定义时保持平均速度不变,标志对于小系统到大规模系统所引起的性能变化;
平均延迟度量标准
一个并行系统执行的时间图谱
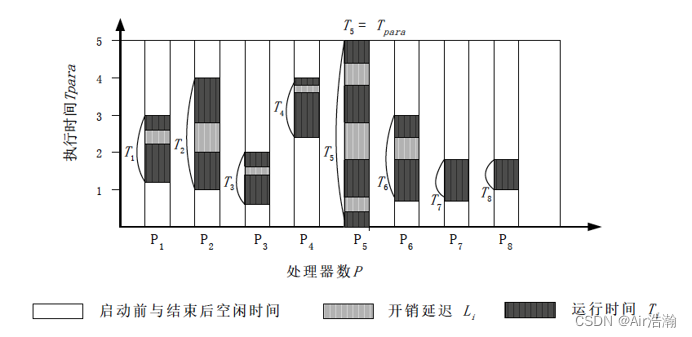
- T p a r a T_{para} Tpara 是最大的,作为总的并行时间

基准评测程序(Benchmark)
不同程序会涉及到硬件、体系结构、编译优化、编程环境、测试条件、解题算法等众多因素;根据侧重点不同,分为:
综合型:Dhrystone、Whetstone
- 缺点:对编译器比较敏感
核心型:Livermore Fortran Kernels、NASA 之 NAS
数学型:Linpack、FFT
- 常见的线性代数运算
应用型:SPEC、Perfect、Splash
并行型:NAS 之 NPB、PARKBENCH
