关于基线长度对双天线GNSS测姿精度的影响
文章目录
- 一、GNSS测姿原理
- 1. 载波相位双差求解基线向量
- 2. GNSS姿态角表示
- 二、基线长度对GNSS测姿精度的影响
- 三、GNSS定向产品精度描述实例
- 四、参考文献
在GNSS定向模块或者板卡的指标参数中,我们一般会看到航向的测量精度和基线的长度相关。在实际使用,用双天线定向想要达到比较理想的精度,基线长度一般会大于50cm。我之前一直有这个意识,但是也没有认真去思考和整理这个问题(虽然对许多人来说,答案也许是显而易见的)。
这篇博客主要是整理一下GNSS定向的原理,以及为什么其精度受到基线长度的影响。如果你也感兴趣的话,就请继续看下去吧。
一、GNSS测姿原理
整体而言,要实现定向,主要就是要求解基线向量。在我理解,其实整个过程和普通的RTK求解没有太大区别,只不过可以多加一个基线约束。
依照我自己的理解,求解过程应该主要包含以下几个步骤:
- 利用伪距双差计算主从天线的位置(一般是分米级),当然也可以是用卡尔曼滤波来计算。理论上,即使位置不是非常准确,对 line of sight 的计算精度影响也不会很大。
- 利用主从天线位置、卫星位置计算 line of sight。计算载波相位双差量测量,组成双差方程,此时方程中未知数包含基线向量和双差整周模糊度。
- 用LAMBDA或者其他算法固定双差整周模糊度,从而求解基线向量。
- 由于基线长度固定,因此可以利用基线长度进行约束。
- 将基线向量由ECEF坐标系转换到地理坐标系,求解航向和俯仰角。
1. 载波相位双差求解基线向量
对于载波相位量测量包含哪些误差之类的,我就不赘述了,随便找本教科书都能找到。下面仅列出单差、双差方程[1]。
单差(站间差)载波相位量测方程:
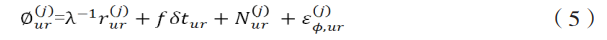
双差(星间差)载波相位量测方程:
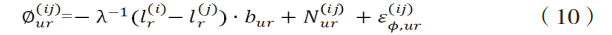
上式中每个量的含义可以参照下图。需要注意的是,我们计算的天线位置、卫星位置、line of sight都是在ECEF坐标系中,因此上式的基线向量也表示在ECEF坐标系。
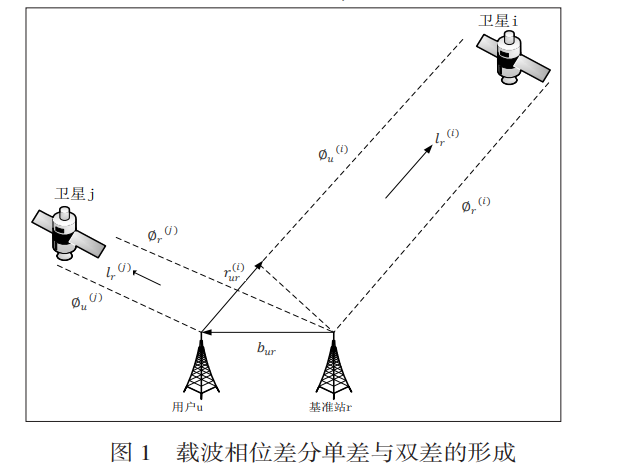
2. GNSS姿态角表示
如果求解得到主从天线在ECEF坐标系中基线向量,可以将其转到当地地理坐标系(如东北天),那么便可以由此计算航向和俯仰角。如下图和公式中所表示的方位角(航向)、高度角(俯仰)。

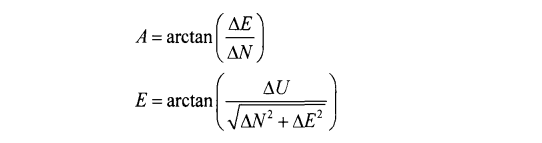
二、基线长度对GNSS测姿精度的影响
参考论文[2], 暂不考虑俯仰角,在水平方向如果基线向量的计算存在误差δp\delta pδp,且误差相对于基线长度 lll 来说比较小,那么航向的误差δθ\delta{\theta}δθ可以用下图的中式(7~8)来表示。
由此可见,基线长度越长,那么航向的误差越小。假设基线的误差是5mm,基线长度为1m,根据式(8)可知,理论上航向的误差为0.286°。俯仰角的误差其实和航向角计算误差类似。


三、GNSS定向产品精度描述实例
(1)以司南的K823定位定向模块为例,其测姿精度如下图所示:
- 如果基线长度为1m,那么方位角精度为0.15°,横滚或俯仰角精度为0.25°。
- 如果基线为两米,则方位角精度为0.075°,横滚或俯仰角精度为0.125°。

(2)北云的高精度组合导航接收机 X2:
- 基线 = 2m,定向精度0.08°
- 基线 = 4m,定向精度0.05°
四、参考文献
[1]夏佩, 王峰, 黄祖德,等. 基于双天线的RTK-GPS定向方法[J]. 中国新通信, 2018, 20(22):3.
[2] Medina D , Heselbarth A , Buscher R , et al. On the Kalman Filtering Formulation for RTK Joint Positioning and Attitude Quaternion Determination[C]// IEEE/ION Plans. IEEE, 2018:597-604.
