强化学习p3-策略学习
Policy Network (策略网络)
我们无法知道策略函数 π \pi π所以要做函数近似,求一个近似的策略函数
使用策略网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ) 去近似策略函数 π ( a ∣ s ) \pi(a|s) π(a∣s)
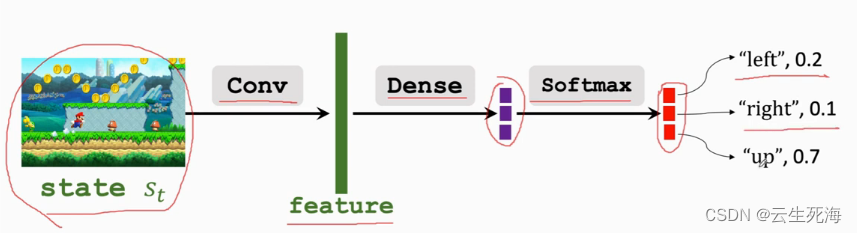
∑ a ∈ A π ( a ∣ s ; θ ) = 1 \sum_{a\in A} \pi(a|s;\theta) = 1 ∑a∈Aπ(a∣s;θ)=1
动作空间A的大小是多少,输出向量的维度就是多少。
策略学习的目标函数
状态价值函数(State-value function)
V π ( s t ) = E A [ Q π ( s t , A ) ] = ∑ a π ( a ∣ s t ) ⋅ Q π ( s t , a ) V_\pi(s_t)=E_A[Q_\pi(s_t,A)] = \sum_a\pi(a|s_t)\cdot Q_\pi(s_t,a) Vπ(st)=EA[Qπ(st,A)]=∑aπ(a∣st)⋅Qπ(st,a)
对A求期望,去掉A的影响
用策略网络 π ( a ∣ s t ; θ ) \pi(a|s_t;\theta) π(a∣st;θ) 去近似策略函数 π ( a ∣ s t ) \pi(a|s_t) π(a∣st)
V π ( s t ; θ ) = E A [ Q π ( s t , A ) ] = ∑ a π ( a ∣ s t ; θ ) ⋅ Q π ( s t , a ) V_\pi(s_t;\theta)=E_A[Q_\pi(s_t,A)] = \sum_a\pi(a|s_t;\theta)\cdot Q_\pi(s_t,a) Vπ(st;θ)=EA[Qπ(st,A)]=∑aπ(a∣st;θ)⋅Qπ(st,a)
近似状态价值既依赖于当前状态 s t s_t st,也依赖于策略网络 π \pi π的参数 θ \theta θ
如果一个策略很好,那么状态价值函数的近似 V π ( s ; θ ) V_\pi(s;\theta) Vπ(s;θ)的均值应当很大。因此我们定义目标函数:
J ( θ ) = E S [ V π ( s ; θ ) ] J(\theta)=E_S[V_\pi(s;\theta)] J(θ)=ES[Vπ(s;θ)]
目标函数 J ( θ ) J(\theta) J(θ) 排除了状态 S S S的因素,只依赖于策略网络 π \pi π的参数 θ \theta θ。策略越好,则 J ( θ ) J(\theta) J(θ) 越大,所以策略学习可以被看作是这样一个优化问题:
m a x θ J ( θ ) \mathop{max}_{\theta}J(\theta) maxθJ(θ)
通过学习参数 θ \theta θ ,使得目标函数 J ( θ ) J(\theta) J(θ)
越来越大,也就意味着策略网络越来越好。
使用策略梯度上升更新 θ \theta θ ,使得 J ( θ ) J(\theta) J(θ)增大。
设当前策略网络的参数为 θ \theta θ,做梯度上升更新参数,得到新的参数 θ ′ \theta' θ′, β \beta β为学习率
θ ′ = θ + β ⋅ ∂ V ( s ; θ ) ∂ θ \theta' =\theta+\beta \cdot \frac{\mathrm{\partial}V(s;\theta)}{\mathrm{\partial}\theta} θ′=θ+β⋅∂θ∂V(s;θ)
策略梯度(Policy Gradient)
∂ V ( s ; θ ) ∂ θ \frac{\mathrm{\partial}V(s;\theta)}{\mathrm{\partial}\theta} ∂θ∂V(s;θ)大概推导 不严谨 实际上 Q π Q_\pi Qπ中也有 θ \theta θ要求导

使用策略梯度更新策略网络
算法:
1、在 t t t时刻观测到状态 s t s_t st
2、根据策略网络 π ( . ∣ s t ; θ ) \pi(.|s_t;\theta) π(.∣st;θ)随机抽样一个动作 a t a_t at
3、计算动作价值 q t ≈ Q π ( s t , a t ) q_t \approx Q_\pi(s_t,a_t) qt≈Qπ(st,at)
4、计算策略网络关于参数 θ \theta θ的微分 d θ = ∂ l n π ( a ∣ s ; θ ) ∂ θ ∣ θ = θ t d\theta = \frac{\mathrm{\partial}ln\pi(a|s;\theta)}{\mathrm{\partial}\theta}|_{\theta=\theta_t} dθ=∂θ∂lnπ(a∣s;θ)∣θ=θt
5、计算近似策略梯度 g ( a t , θ t ) = q t , d θ g(a_t,\theta_t)=q_t,d\theta g(at,θt)=qt,dθ
6、更新策略网络: θ t + 1 = θ t + β ⋅ g ( a t , θ t ) \theta_{t+1}=\theta_t+\beta \cdot g(a_t,\theta_t) θt+1=θt+β⋅g(at,θt)
在第 3 步中,怎么计算 q t q_t qt?
在后面章节中,我们用两种方法对 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a) 做近似。
1、REINFORCE 算法
用实际观测的回报 u u u近似 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a)。
2、actor-critic 算法
用神经网络 q ( s , a ; w ) q(s,a;w) q(s,a;w)近似 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a)。
所以想要近似求得 π \pi π函数 还要近似求得 Q π Q_\pi Qπ函数
