f(x)与|f(x)|,f ‘ (x),F(x)常见关系。
1.f(x)与|f(x)|关系。
1.连续关系。(f(x)在"[a,b]上连续" => |f(x)|在"[a,b]连续")
①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. (因为f(x)在x0的连续点=>x0必为|f(x)|的连续点)
注:”[a,b]连续“包括:①f(x)在[a,b]连续②f(x)在[a,b]上有界,且仅有有限间断点③f(x)在[a,b]只有有限个第一类间断点。
证明:f(x)在"[a,b]上连续" => |f(x)|在"[a,b]连续"

2.可积关系。(f(x)可积 => |f(x)|可积)
证明略。
反例:
f(x)有无限个间断点,f(x)不可积。但是|f(x)|可积。
3.可导关系。
①f(x)在x0可导,则当f(x0) ≠ 0时
f(x)可导 <=> |f(x)|可导
②f(x)在x0可导,则当f(x0) = 0时,有两种情况。
-------1.若f’(x₀) = 0,则 <=> |f(x)| 在点x₀处可导,且|f’(x₀)|=0。
-------2.若f’(x₀) ≠ 0,则| f(x)|在点x₀处不可导
证明当f’(x0) ≠ 0时,不成立。成立同样如此证明
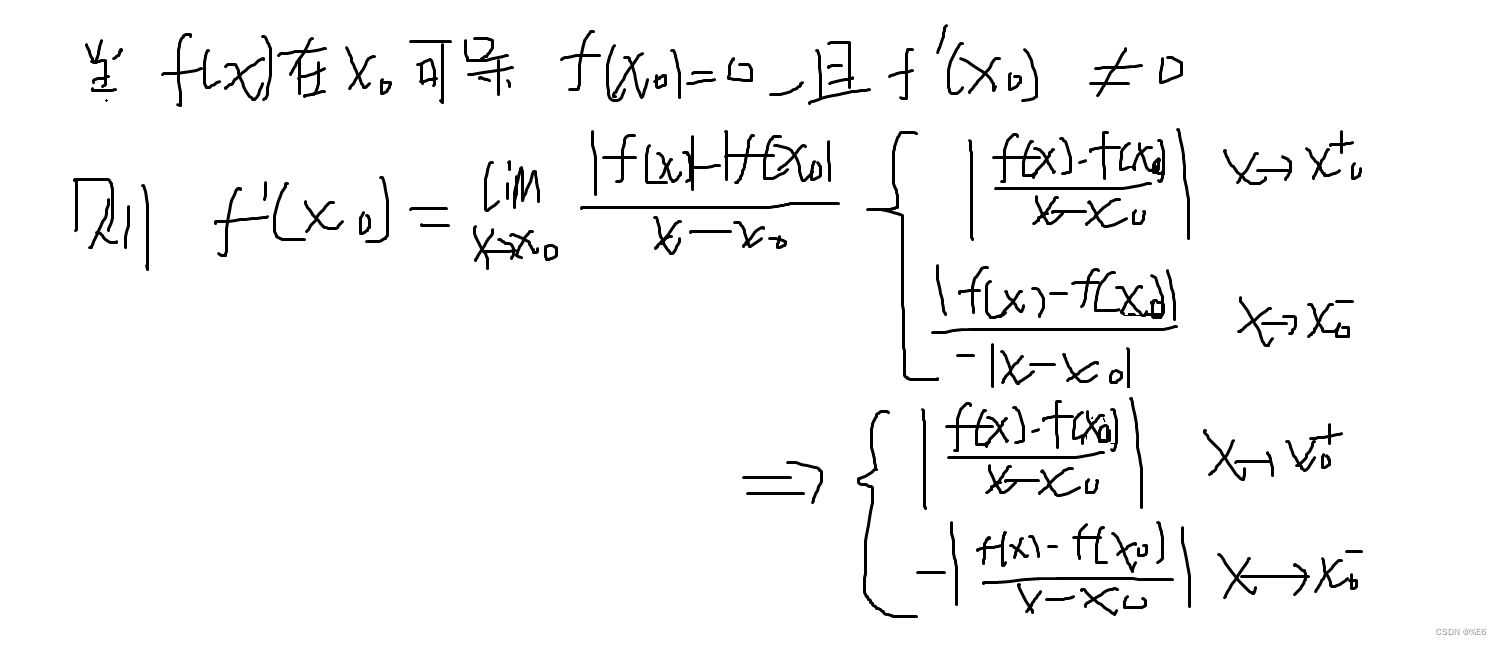
2.f(x)与f ’ (x)关系。
在有界区间(a,b)上有如下关系:
①f ‘(x)在(a,b)上有界 => f(x) 在(a,b)一定有界。
②f (x) 在(a,b)上无界 => f ’ (x)在(a,b)一定无界。
③设f(x) 在 x = a 处n阶可导,若当x - > a时f(x)是x - a 的n阶无穷小,则 f ’ (x)是 x - a 的n - 1 阶无穷小。
证明①:②类似

证明③:
在无界区间上没有确定性关系:
若f(x) = x,则f ’ (x) = 1在(a,+∞)有界,但f(x)在(a,+∞)无界。
若f(x) = sin2x,则f(x)在(a,+∞)有界,但是f ’ (x)在(a,+∞)无界。
3.f(x)与F(x)关系。
f(x)在(a,b)上有原函数F(x),则在(a,b)上:
①f(x)不一定连续
②f(x)不一定时初等函数
③F(x)不一定时初等函数
④F’(x) = f(x),因此F(x)连续
4.f(x)与其对应的变上限积分∫ f(t) dt(积分限a到x)关系。

①设x->a时候 , f(x) 是 x - a 的 n 阶无穷小。若f(x)连续,则 ”∫ f(t) dt(积分限a到x)(图片)“ 是 x - a 的 n + 1阶无穷小。
5.lim(x->x0)f’(x)与f’(x0)关系。
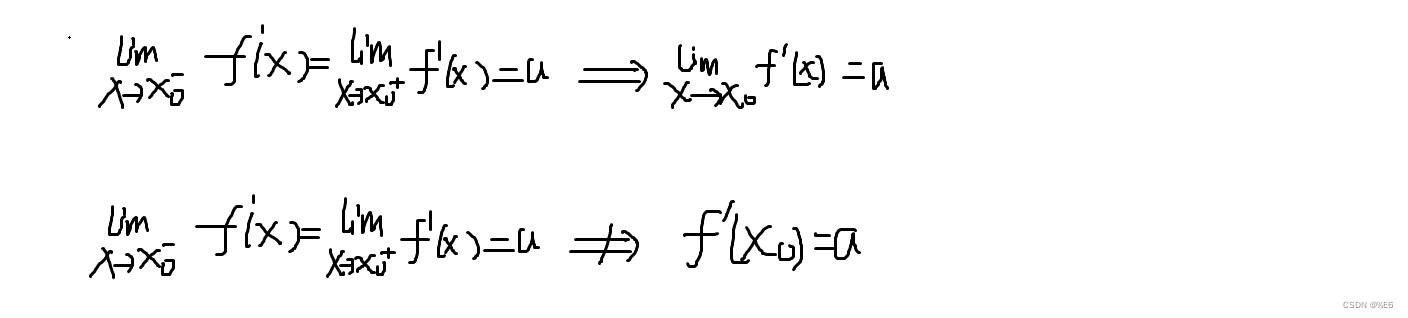
注意:连续的定义:如果f(x)在X0左右极限相等 <=> 在f(x) 在 X0连续 <=>该点的极限 = 该点的函数值。仅适用于f(x),而不适用于任意阶导数。
因为f(x)不能保证在 X0 点可导,甚至连续,极限存在都保证不了,故不能直接推出导数存在。
针对上述有总结以下情况:
1.f(x)在 X0 可导 => f(x) 在 X0 连续。(可导必连续)
2.lim f ’ (x) 存在 =/> f(x)在 X0 连续。(在 x -> X0时 上述有解释)
3.设 f (x) 在 x - > X0的空心领域内可导,且 lim f(x) = A (x -> X0) :
①若f(x) 在 x = x0 不连续 => f ’ (x0) 不存在。(不连续肯定不可导)
②若f(x) 在 x = x0 连续 => f’ (x0) = A。
证②:

4.设 f (x) 在 x - > X0的空心领域内可导,且 lim f ’ (x) = ∞ (x -> x0):
①若f(x) 在 x = x0 不连续 => f ’ (x0) 不存在。(不连续肯定不可导)
②若f(x) 在 x = x0 连续 => f’ (x0) = ∞ 。(仍然洛必达证)
5.设 f (x) 在 x - > X0的空心领域内可导,且 lim f ’ (x) = 不存在 (x -> x0):
看题,暂时没结论。
