经典数据结构之2-3树
2-3树定义
2-3树,是最简单的B-树,其中2、3主要体现在每个非叶子节点都有2个或3个子节点,B-树即是平衡树,平衡树是为了解决不平衡树查询效率问题,常见的二叉平衡书有AVL树,它虽然提高了查询效率,但是插入操作效率不高,因为它需要再每次插入节点后维护树的平衡,而为了解决查询效率同时有兼顾插入效率,于是提出了2-3树。
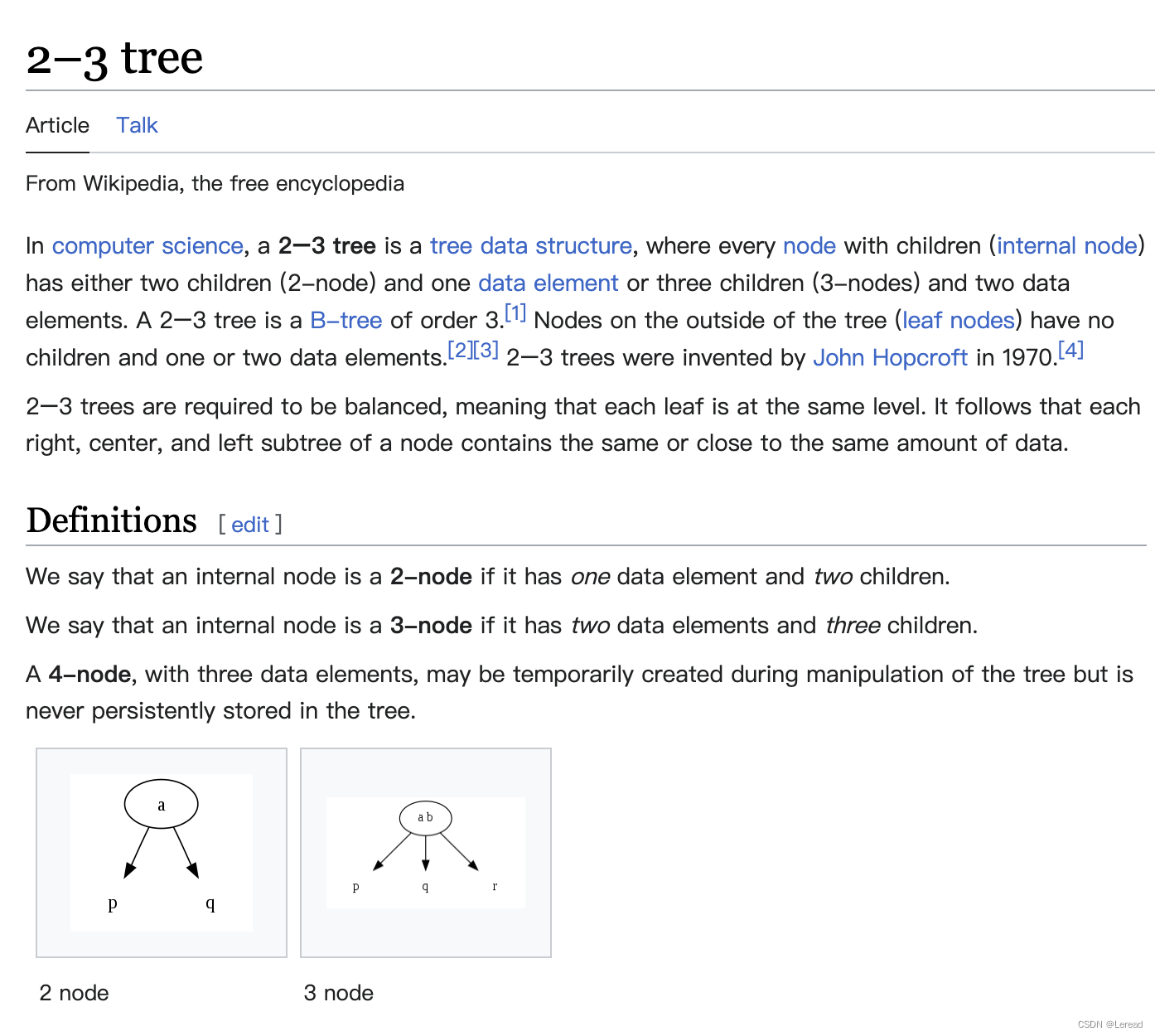
2-3树特点
- 2-3树是一棵平衡树,但不是二叉平衡树。
- 对于高度相同的2-3树和二叉树,2-3树的节点数要大于满二叉树,因为有些节点可能有三个子节点。
- 2-3树可以是一棵空树。
- 对于2节点来说,该节点保存了一个key及对应的value,除此之外还保存了指向左右两边的子节点,子节点也是一个2-3节点,左子节点所有值小于key,右子节点所有值大于key。
- 对于3节点来说,该节点保存了两个key及对应的value,除此之外还保存了指向左中右三个方向的子节点,子节点也是一个2-3节点,左子节点的所有值小于两个key中较小的那个,中节点的所有值在两个key值之间,右子节点大于两个key中较大的那个。
- 对2-3树进行中序遍历能得到一个排好序的序列。
2-3树查找
2-3 树的查找类似二叉搜索树的查找过程,根据键值的比较来决定查找的方向。
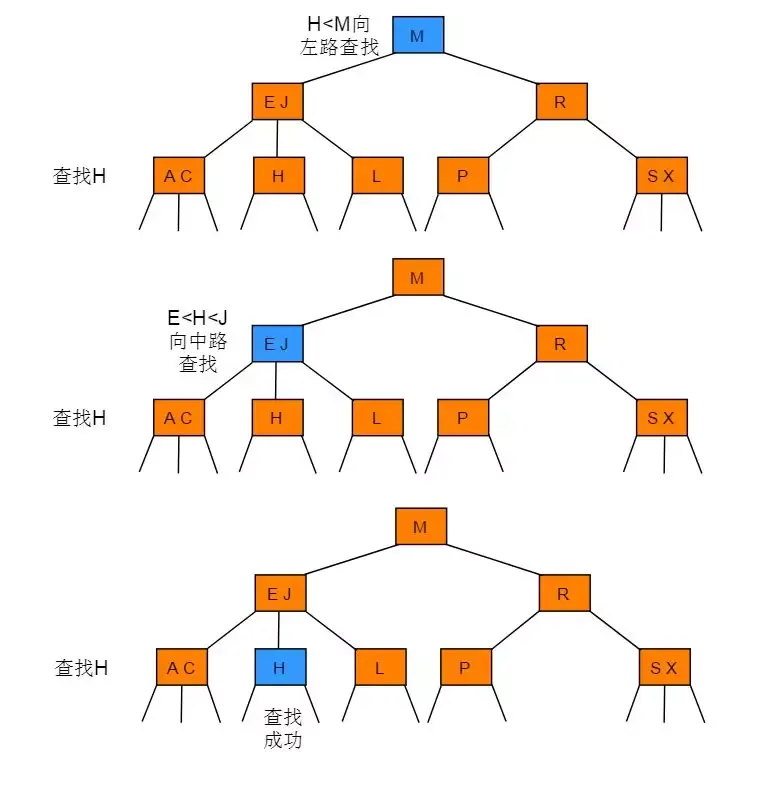
例如在图 2.1 所示的 2-3 树中查找键为H的节点:
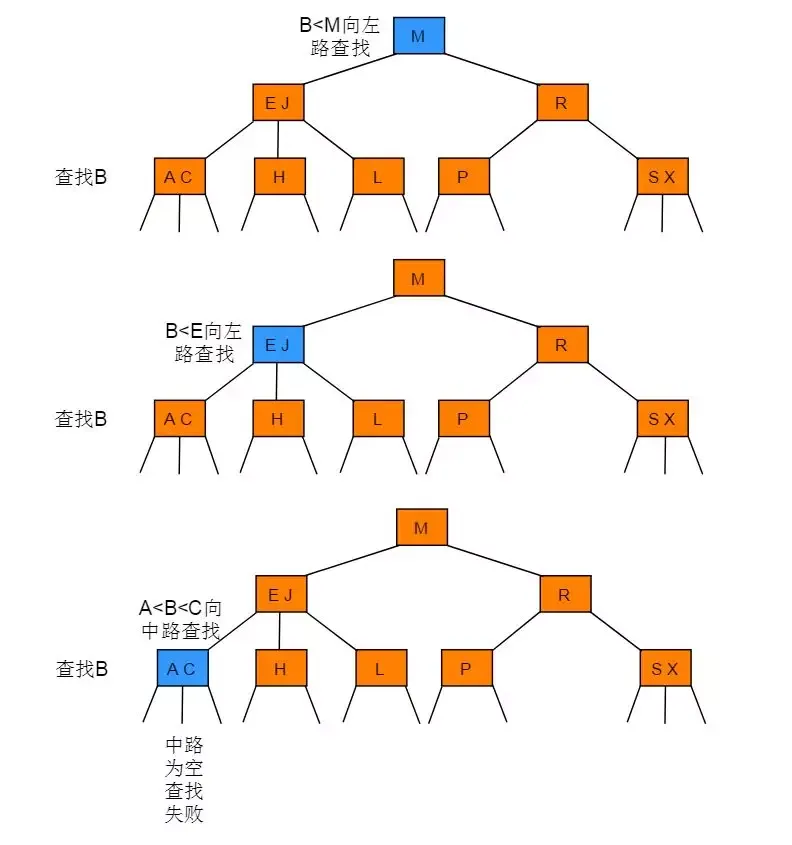
例如在图 2.1 所示的 2-3 树中查找键为 B 的节点:
2-3树插入
插入
在树的插入之前需要对带插入的节点进行一次查找操作,若树中已经有此节点则不予插入,若没有查找到此节点则记录未命中查找结束时访问的最后一个节点。
空树的插入最简单,创建一个节点即可,这里不予赘述。
对于非空树插入主要分为 4 种情况:
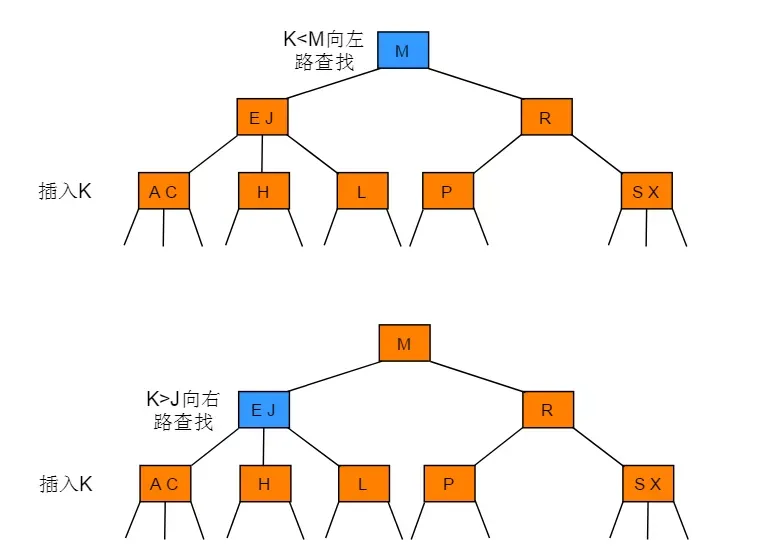
(1)向 2- 节点中插入新节点
(2)向一棵只含 3- 节点的树中插入新节点
(3)向一个父节点为 2- 节点的 3- 节点中插入新节点
(4)向一个父节点为 3- 节点的 3- 节点中插入新节点
向2-节点中插入新节点
操作步骤:如果未命中查找结束于一个 2-节点,直接将 2- 节点替换为一个 3- 节点,并将要插入的键保存在其中。
图解:
向一棵只含 3- 节点的树中插入新节点
操作步骤:先临时将新键存入唯一的 3- 节点中,使其成为一个 4- 节点,再将它转化为一颗由 3 个 2- 节点组成的 2-3 树,分解后树高会增加 1。
图解:
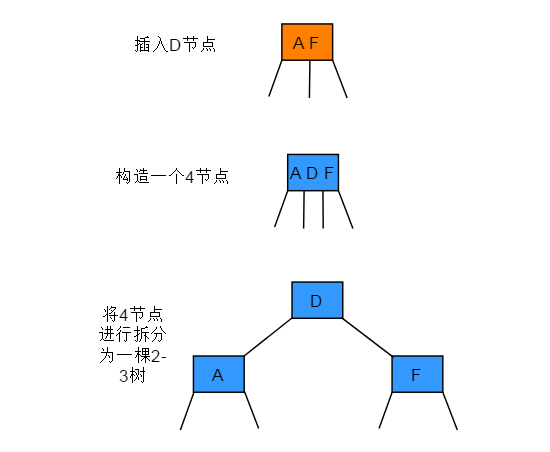
向一个父节点为 2- 节点的 3- 节点中插入新节点
操作步骤:先构造一个临时的 4- 节点并将其分解,分解时将中键移动到父节点中(中键移动后,其父节点中的位置由键的大小确定)
图解:
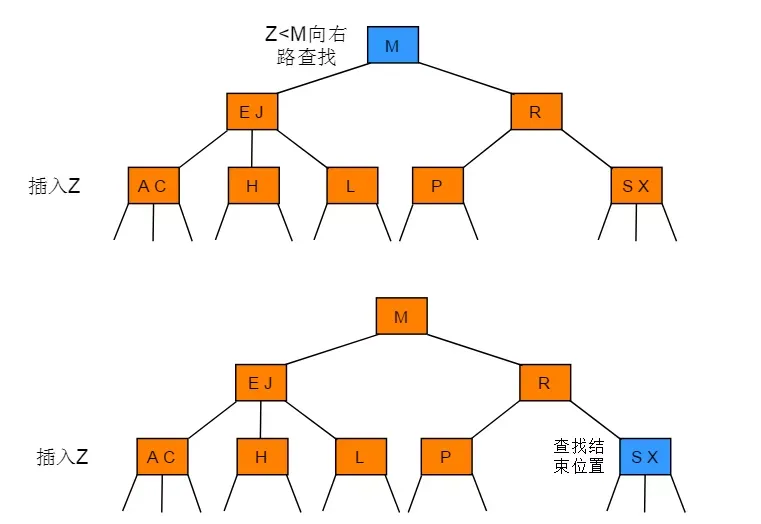
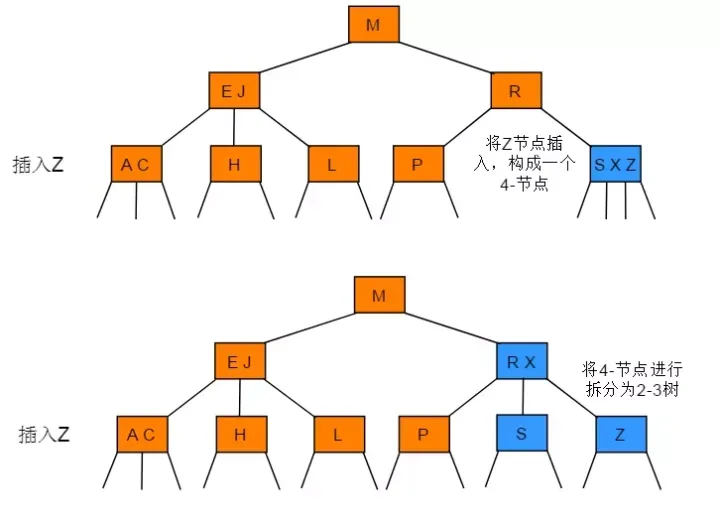
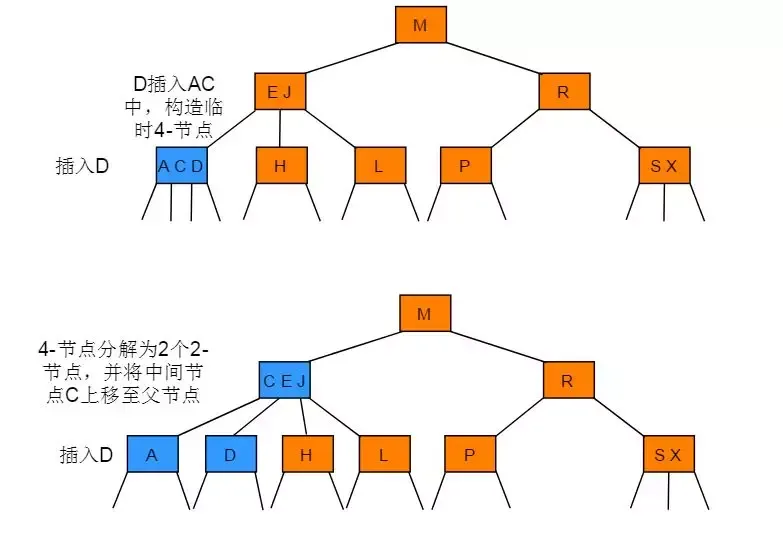
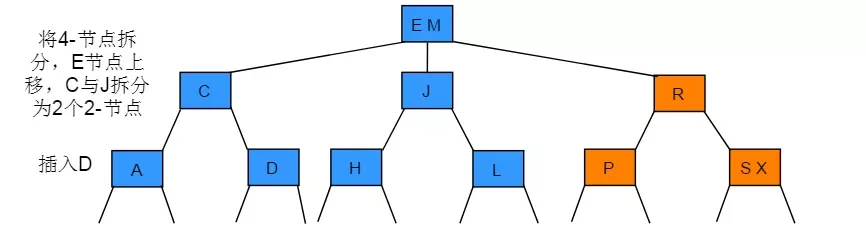
向一个父节点为3-节点的3-节点中插入新节点
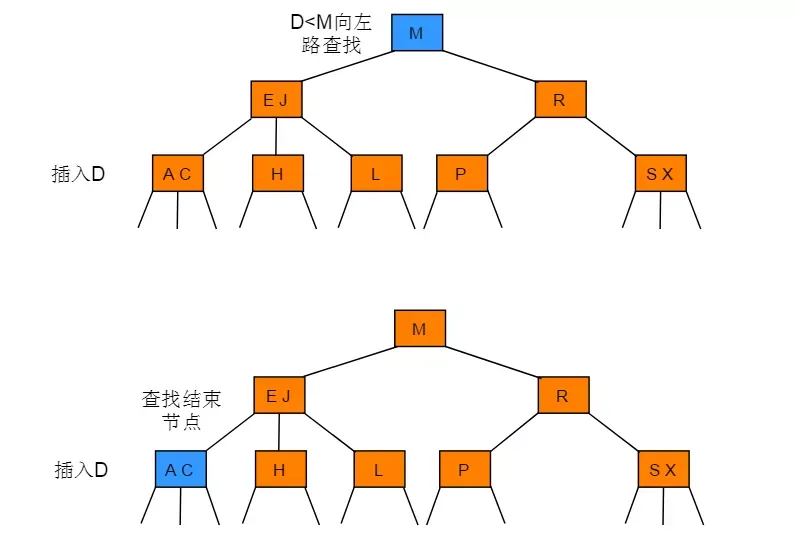
操作步骤:插入节点后一直向上分解构造的临时4-节点并将中键移动到更高层双亲节点,直到遇到一个-2节点并将其替换为一个不需要继续分解的3-节点,或是到达树根(3-节点)。
图解:
总结
2-3 树作为一种平衡查找树,查询效率比普通的二叉排序树要稳定许多。但是2-3树需要维护两种不同类型的结点,查找和插入操作的实现需要大量的代码,而且它们所产生的额外开销可能会使算法比标准的二叉查找树更慢。
