下降路径最小和

dp问题描述

下降路径最小和

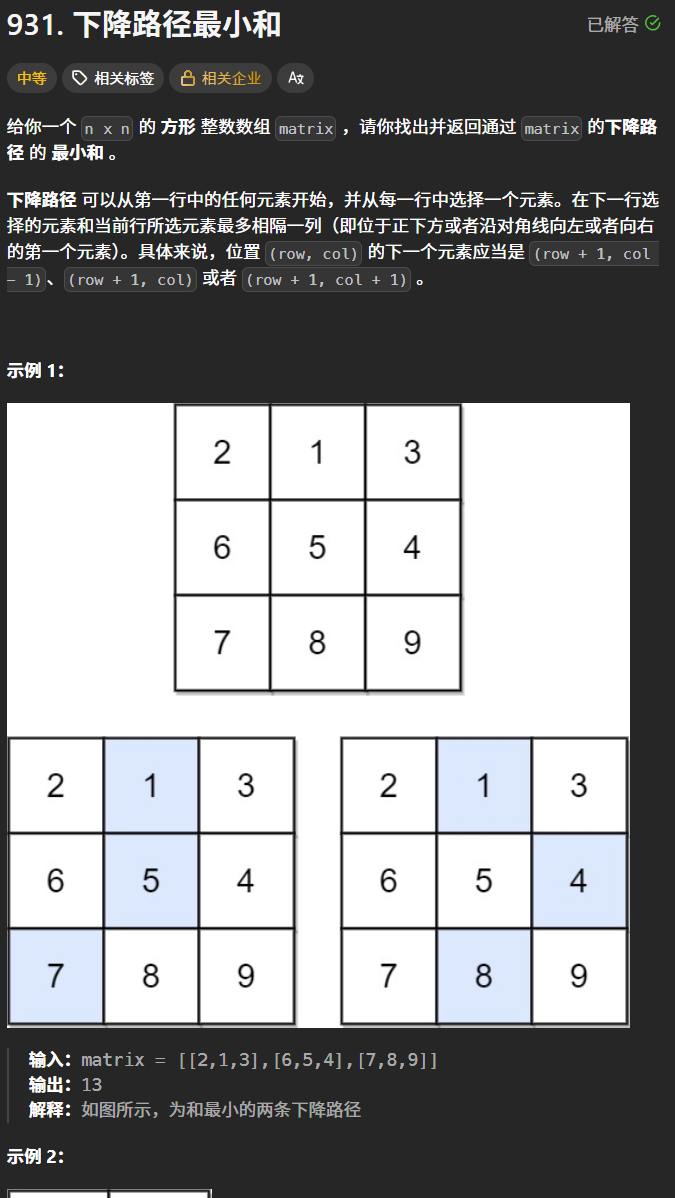
确定本题的状态表示

dp[i][j]表示的是从第一层中的任意位置下降到(i,j)位置处的下降路径最小和

确定本题的状态转移方程

本题的状态转移方程是：
dp[i][j]=min({dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1]})+min_up+matrix[i-1][j-1];
但是在实际实现的时候是要注意边界情况，即 j==1和j==n时，我们最右边和最左边的dp数组就不要再加进来比了，容易造成越界访问，即使没有越界访问，因为比的是最小值，最外围的dp数组元素都是0，一比就把有效数据消除了

填表求值

根据初始条件和状态转移方程，确定填表顺序，进而逐步填满dp表，最终返回题目要的结果

代码实现

class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int m=matrix.size();if(m==0) return 0;int n=matrix[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1,0));for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){int min_up;if(n==1) min_up=dp[i-1][1];else if(j==1) min_up=min({dp[i-1][j],dp[i-1][j+1]});else if(j==n) min_up=min({dp[i-1][j-1],dp[i-1][j]});else min_up=min({dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1]});dp[i][j]=min_up+matrix[i-1][j-1];}}int ret=dp[m][1];for(int j=1;j<=n;j++) {if(ret>dp[m][j]) ret=dp[m][j];}return ret;}
};