[优选算法专题二滑动窗口——最大连续1的个数 III]
题目链接
最大连续1的个数 III
题目描述

题目解析
问题本质
- 输入:二进制数组
nums(只包含 0 和 1)和整数k - 操作:最多可以将
k个 0 翻转成 1 - 目标:找到翻转后能得到的最长连续 1 的子数组长度
这个问题的核心是要找到一个区间,在允许翻转最多k个 0 的情况下,这个区间内的 1(包括翻转得到的 1)是最长的。
解题思路:滑动窗口法
滑动窗口(双指针)是解决这类 "最长连续子数组" 问题的高效方法,基本思想是:
- 用两个指针
left和right维护一个区间(窗口)[left, right] - 保证窗口内的 0 的数量不超过
k(即可以通过翻转使整个窗口都变为 1) - 不断扩大窗口(移动
right),当窗口不满足条件时缩小窗口(移动left) - 记录过程中出现的最大窗口长度
算法流程:
1. 初始化: left = 0 , right = 0 , ret = 0 ;
2. 当 right ⼩于数组⼤⼩的时候,⼀直下列循环:
i:进窗口,1无视,0计数表++;
ii:判断计数表是否 >k;
是则让左侧元素滑出窗⼝,更新哈希表的值,直到 0 的个数恢复正常;
iii:更新结果,right++;
3. 循环结束后, ret 存的就是最终结果。

关键代码逻辑解析
// 当窗口中0的数量超过k时,需要缩小窗口 while(zero > k) {if(nums[left++] == 0) zero--; }
这段代码是算法的核心,它确保了窗口的合法性:
- 当 0 的数量超过 k 时,通过移动左指针缩小窗口
- 只有当移除的元素是 0 时,才减少
zero的计数 - 循环结束后,窗口内 0 的数量一定≤k
ret = max(ret, right - left + 1);
这行代码用于更新最长有效窗口的长度,每次移动右指针后都要检查当前窗口是否是最长的。
完整代码
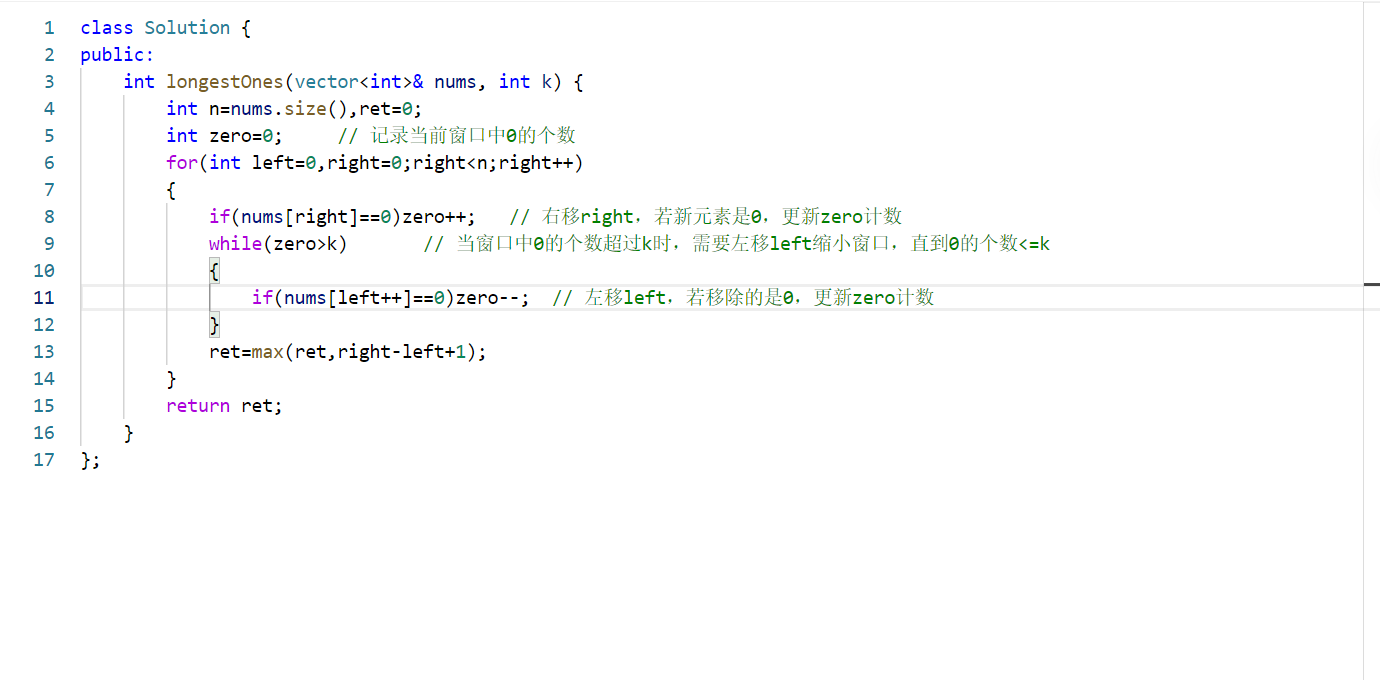
算法优势分析
-
时间效率:
- 每个元素最多被
left和right各访问一次 - 总时间复杂度为 O (n),n 为数组长度
- 相比暴力解法(尝试所有可能的子数组)的 O (n²) 有显著提升
- 每个元素最多被
-
空间效率:
- 只使用了常数个额外变量(
left、right、zero、ret等) - 空间复杂度为 O (1)
- 只使用了常数个额外变量(
