数据结构——单链表oj（续）

链表分割_牛客题霸_牛客网

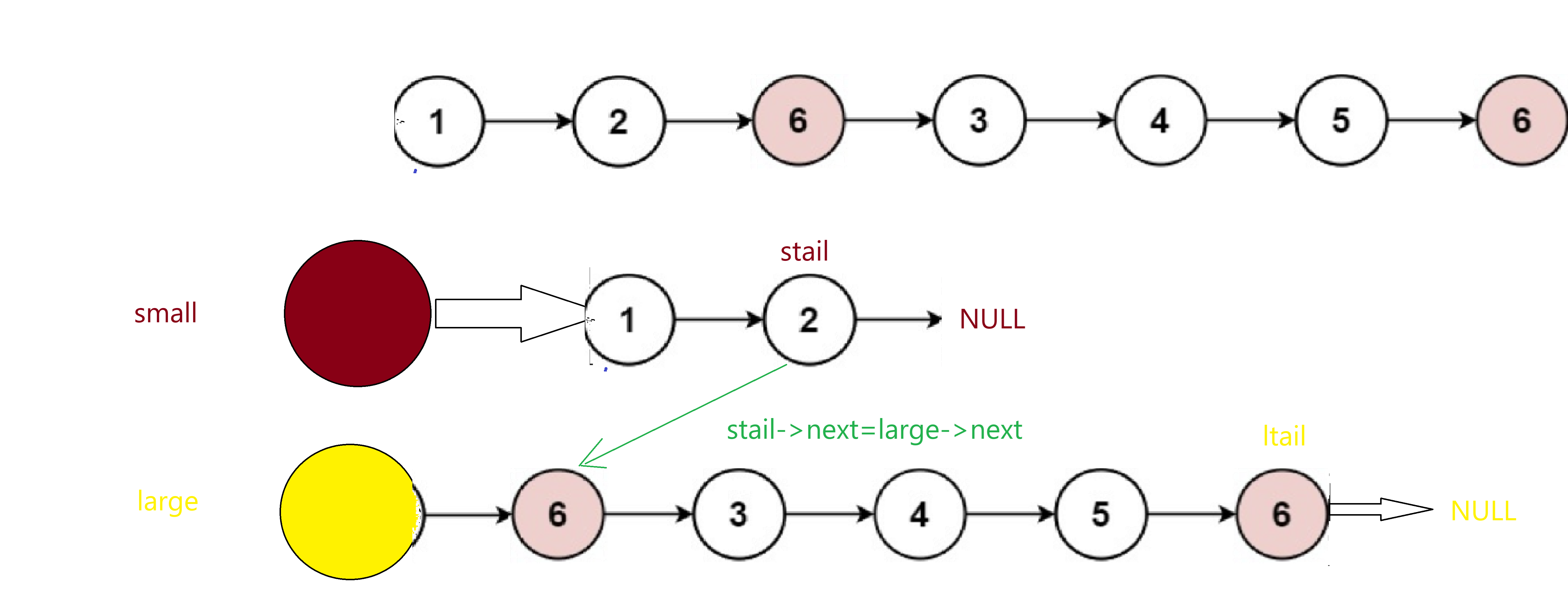
解题思路：创建两个新链表，为两个新链表各自申请一个空头结点，然后将值比x小的节点尾插到其中一个新链表之后，值比x大的尾插到另外一个新链表之后，最后将两个链表连接起来即可：

typedef ListNode ltnode;
class Partition {
public:ListNode* partition(ListNode* pHead, int x) {// write code hereif(pHead==NULL){return NULL;}//申请两个空头结点ltnode*small=(ltnode*)malloc(sizeof(ltnode));ltnode*large=(ltnode*)malloc(sizeof(ltnode));large->next=NULL;small->next=NULL;//尾结点ltnode*stail=small,*ltail=large;ltnode*pcur=pHead;while(pcur){if(pcur->val<x){stail->next=pcur;stail=stail->next;}else {ltail->next=pcur;ltail=ltail->next;}pcur=pcur->next;}stail->next=NULL;ltail->next=NULL;stail->next=large->next;return small->next;}
};

160. 相交链表 - 力扣（LeetCode）

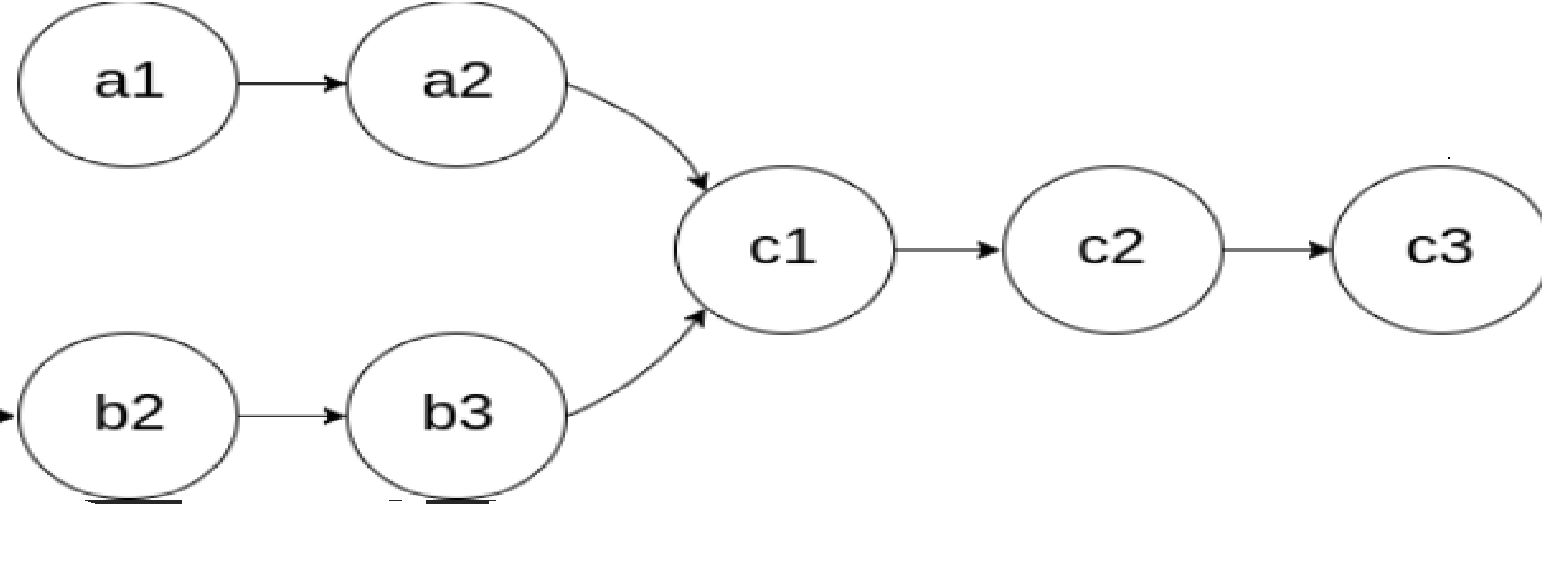
假设两个链表长度相同，那么分别用两个指针指向两个链表的第一个节点，各自往后遍历，如果两个链表相交，那么这两个指针一定会出现指向相同的情况。

如果链表长度不相同，我们还想用上面的原理应该怎么做？那就让指向链表长度较长的那个链表的第一个节点的指针先往后走，走到什么程度为止呢？直到这个指针指向的位置到链表尾结点的长度与指向短链表的第一个节点的指针到链表尾结点的长度相同为止，也就是让长链表的那个指针先走（长链表-短链表）个步长，然后再让两个指针一起走，如果两个指针会指向相同，就说明相交，反之不相交。

 #include<stdlib.h>typedef struct ListNode ltnode;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{ltnode* pcur1 = headA ;ltnode* pcur2 = headB ;int len1=0,len2=0;while(pcur1){len1++;pcur1=pcur1->next;}while(pcur2){len2++;pcur2=pcur2->next;}int len=abs(len1-len2);
//假设长链表是A链表ltnode* longlist = headA;ltnode* shortlist= headB;
//如果假设不成立if(len1<len2){longlist = headB;shortlist= headA;}pcur1=longlist;pcur2=shortlist;while(len--){pcur1=pcur1->next;}while(pcur1){if(pcur1==pcur2){return pcur1;}pcur1=pcur1->next;pcur2=pcur2->next;}return NULL;
}

141. 环形链表 - 力扣（LeetCode）

这一题我们使用快慢指针来做，先说明快慢指针是一定能解决这一道题的，等到给出代码以后，我们再给出数学证明。

先来说明一下为啥能使用快慢指针的方法来解决这道题？因为快指针每次都比慢指针多走些距离，那么快指针一定会比慢指针先入环，当慢指针入环的时候，快指针已经在环内转了一段时间了，于是快指针就和慢指针开始了追击相遇的过程，那么在一定的速度差下，快指针和慢指针就一定能相遇，相遇就说明链表是成环的。

 typedef struct ListNode ltnode;
bool hasCycle(struct ListNode *head)
{ltnode*fast=head,*slow=head;//现在让fast每次走两步，slow每次走一步，如果链表中没有环，那么最终就会出现fast为空或者fast->next为空的情况，这个就是循环的结束条件while( fast && fast -> next ){slow=slow->next;fast=fast->next->next;if(slow==fast){return true;}}return false;
}

现在就让我们一起来证明：为什么快指针每次走两步，慢指针每次走一步快慢指针就一定能够相遇？

假设slow刚要入环时，fast与slow相距为N，如图我们将链表抽象化：

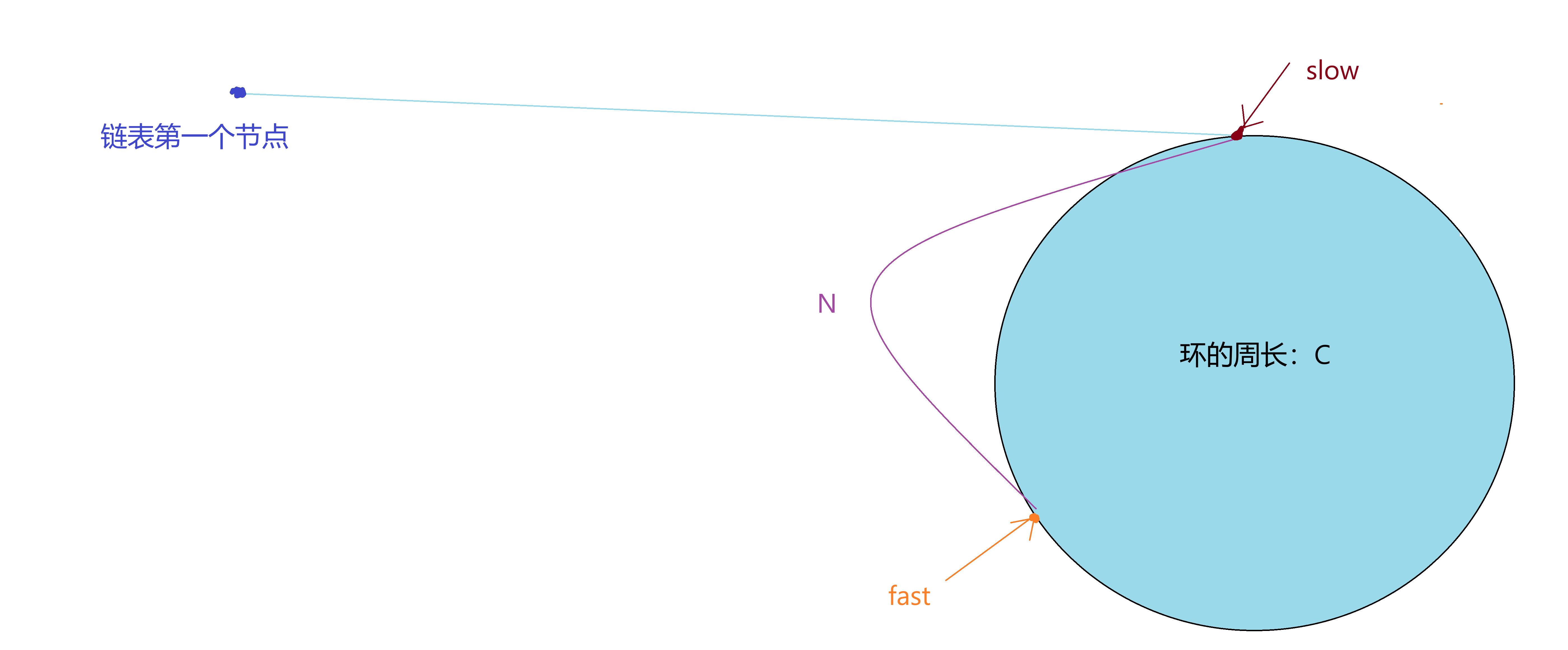
此后slow每走一步，快指针就走两步，那么快指针与慢指针的距离就变成了（N+1-2）=（N-1），也就是说fast和slow每走一次，fast和slow的距离就会缩减1步，那么他们间的距离的变化就是

N,N-1,N-2……2,1,0

也就是说fast和slow最终的距离会变成0，即fast和slow会在slow入环的第一圈相遇。

如果慢指针每次走一步，快指针每次走3步、4步、5步……快慢指针还会相遇吗？

我们来看看快指针每次走3步他们是否还会相遇：

假设slow刚要入环时，fast与slow相距为N，此后slow每走一步，快指针就走三步，那么快指针与慢指针的距离就变成了（N+1-3）=（N-2），也就是说fast和slow每走一次，fast和slow的距离就会缩减2步，那么他们间的距离的变化就是

N,N-2,N-4,N-6……

他们距离最终会变成0吗，不一定。如果N是偶数的话，距离的最终结果会变成0，说明fast和slow会在slow入环的第一圈相遇。如果是奇数，那么他们的距离最终会变成3、1、-1，当距离为-1的时候，说明fast又跑到了slow的前面，又需要开启新一轮追逐，假设环的长度为C，那么新一轮追逐开启时，slow和fast的距离为C-1，如果这一轮追逐两个指针还是无法相遇，那么他们就再也无法相遇了。

前面我们已经说过了，当fast每次走三步时，有：

开启追逐时，如果N（fast与slow的距离）为奇数，就无法在这一轮相遇；

                     如果N是偶数，那就可以相遇。

所以，我们有，如果C-1是奇数，即C是偶数，那么就无法相遇

                         如果C-1是偶数，即C是奇数，那么就可以相遇。

现在我们的问题就转化为求证C究竟是偶数还是奇数：

我们知道，slow和fast的路程由他们的速度决定，所以有：3*slow的路程=fast的路程。

当slow刚要入环的时候，fast可能已经在环里面绕了很多圈了，假设已经绕的圈数为n，那么slow刚入环时就有：3*L=L+C-N+n*C.(L表示第一个节点到入环节点的长度）

化简后，有：2*L+N=(n+1)*C，我们知道2*L是偶数，N是奇数，所以2*L+N是奇数，那么（n+1）*C就恒为奇数。奇数可以由偶数与某个数相乘得到吗？不行，所以n+1和C就都是奇数。

综上，C是奇数，说明如果N是奇数，那么两个指针一定可以在第二轮追逐中相遇。

所以当fast每次走三步，slow每次走一步时，两个指针一定可以相遇。

我们可以用类似的方法去证明当fast每次走4步、5步……，fast和slow都能在环中相遇。

我们再来写一下fast每次走三步的代码：

 typedef struct ListNode ltnode;
bool hasCycle(struct ListNode *head)
{ltnode*fast=head,*slow=head;while( fast && fast -> next && fast->next->next ){slow=slow->next;fast=fast->next->next->next;if(slow==fast){return true;}}return false;
}

142. 环形链表 II - 力扣（LeetCode）

这道题的做法有点不太好想，小编在这里就直接给出一个结论，利用这个结论我们可以很快的解决这个问题：快慢指针在环中的相遇点到入环节点的距离等于第一个节点到入环节点的距离。

 typedef struct ListNode ltnode;
struct ListNode *detectCycle(struct ListNode *head) 
{ltnode*fast=head,*slow=head;ltnode*pcur=head;while( fast && fast -> next ){slow=slow->next;fast=fast->next->next;if(slow==fast){while(pcur!=slow){pcur=pcur->next;slow=slow->next;}return pcur;}}return NULL;
}