算法提升之树上问题-（tarjan求LCA）

今天分享的是另一种求解LCA的方法，通过tarjan求解LCA，关键是要理解具体流程图才可以解决这个问题。

1.基本过程（注意自底往上这个细节点）

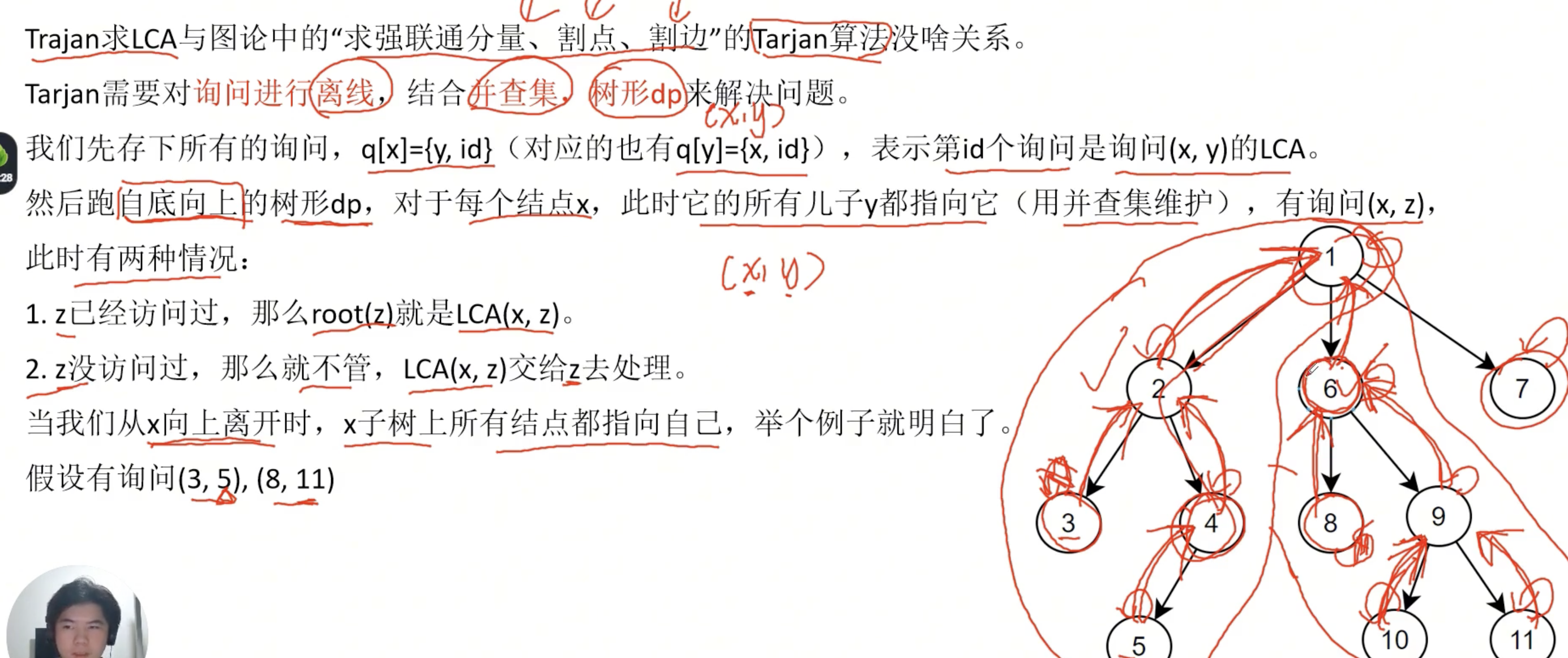
2.基本代码

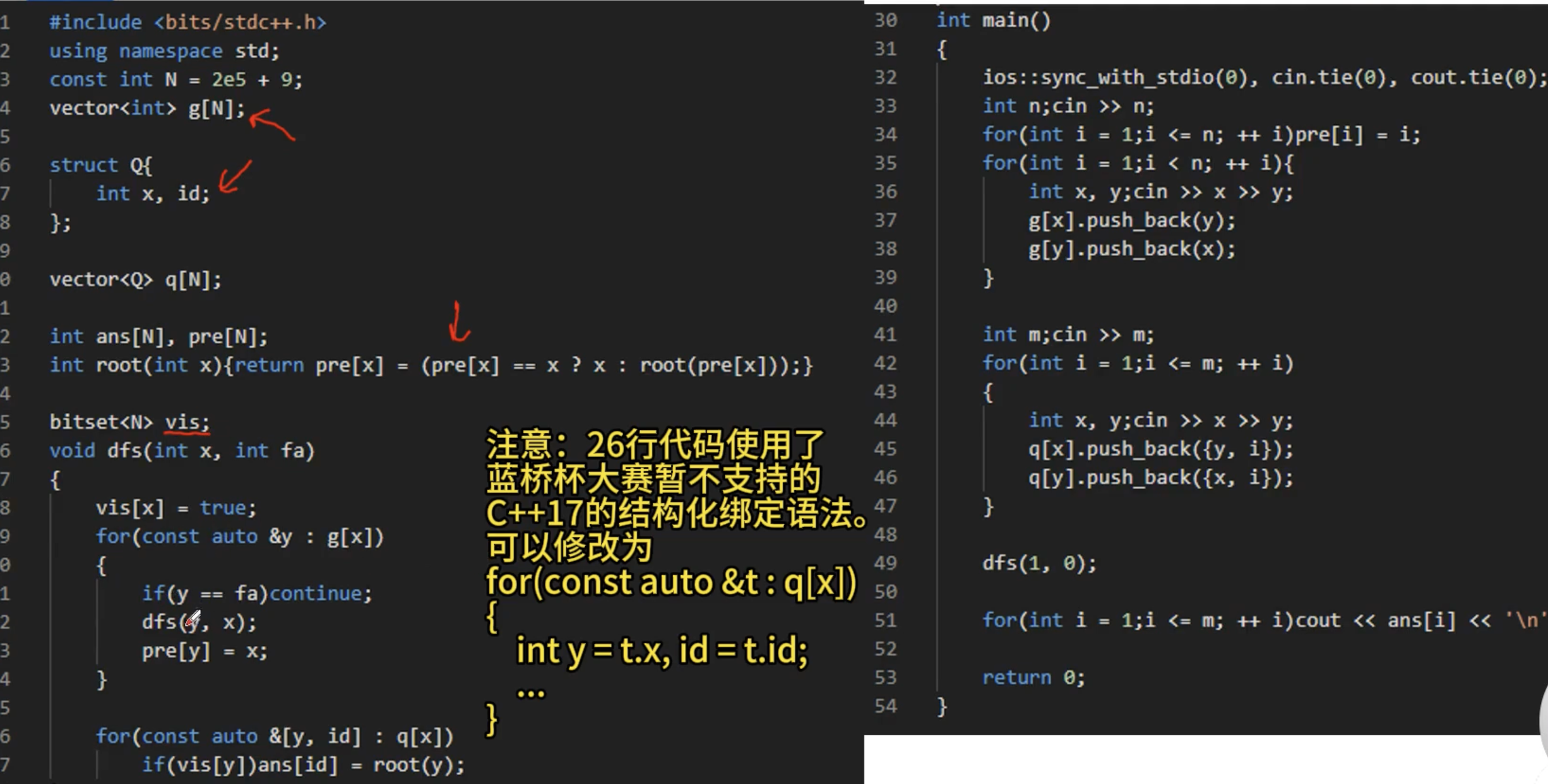
问题描述

给定一棵有 N 个节点的树，每个节点有一个唯一的编号，从 1到 N。树的根节点是 1 号节点。接下来，你会得到 Q 个查询。对于每个查询，你将得到两个节点的编号，你的任务是找到这两个节点的最低公共祖先。

输入格式

第一行包含一个整数 N，表示树的节点数。

接下来的 N−1行，每行包含两个整数 U和 V，表示节点 U 和节点 V 之间有一条边。

下一行包含一个整数 Q，表示查询的数量。

接下来的 Q行，每行包含两个整数 A和 B，表示你需要找到节点 A 和节点 B 的最低公共祖先。

输出格式

对于每个查询，输出一行，该行包含一个整数，表示两个节点的最近公共祖先。

输入案例：

5
1 2
1 3
2 4
2 5
3
4 5
3 4
3 5

输出案例

2
1
1

代码部分

#include <bits/stdc++.h>using namespace std;
const int N = 1e5 + 10;
int h[N], e[2 * N], ne[2 * N], idx, n, root, q;
vector<int> p[N], id[N];
int fa[N], ans[N];
bool st[N];
void add(int u, int v) {e[idx] = v;ne[idx] = h[u];h[u] = idx++;
}
int find(int x) {return fa[x] = fa[x] == x ? x : find(fa[x]);
}
void tarjan(int u) {for (int i = 0; i < p[u].size(); i++) {int j = p[u][i];if (st[j]) {ans[id[u][i]] = find(j);}}st[u] = true;for (int i = h[u]; ~i; i = ne[i]) {int j = e[i];if (st[j]) continue;tarjan(j);fa[j] = u;}
}
int main() {memset(h, -1, sizeof h);cin >> n;for (int i = 1; i <= n; i++) fa[i] = i;for (int i = 0; i < n - 1; i++) {int u, v;cin >> u >> v;add(u, v), add(v, u);}cin >> q;for (int i = 0; i < q; i++) {int a, b;cin >> a >> b;if (a == b) ans[i] = a;else {p[a].push_back(b), p[b].push_back(a);id[a].push_back(i), id[b].push_back(i);}}tarjan(1);for (int i = 0; i < q; i++) cout << ans[i] << '\n' ;return 0;
}

今天的分享就到这里，希望大家可以多多关注，后续也将继续相关内容学习。