十分钟学会一个算法 —— 快速排序
目录
一、工作原理
二、代码实现
三、快速排序的性能
快速排序(Quick Sort)是一种基于分治法的排序算法,通常被认为是最快的排序算法之一,尤其是在实际应用中。其基本思想是通过一个分区操作将数组分成两部分,然后递归地对这两部分进行排序。
快速排序是一种常用的排序算法,平均运行时间为 O(n*log n),只有在最糟糕情况下运行时间为 O(n²) ,平均用时比选择排序要快得多。快速排序也使用了分治思想,一般使用递归实现。
不了解递归和分治算法的,我前面写了两篇博客可以看一下了解了解。一种常用的算法设计方法 —— 递归-CSDN博客文章浏览阅读527次,点赞12次,收藏10次。递归是一种通过调用自身解决具有相似性子问题的重要编程方法。文章首先通过文件夹处理的例子对比了循环和递归两种实现方式,指出递归能使代码更简洁易读但可能带来栈溢出风险。其次阐述了递归的两个核心要素:递归条件(调用自身)和基线条件(终止条件)。最后以阶乘函数为例,展示了递归的实现过程,其中n==1作为基线条件终止递归。理解递归需要掌握其适用场景、实现原理及终止条件。https://blog.csdn.net/a1547998353/article/details/149975465?spm=1001.2014.3001.5501一种通用的问题解决方法 —— 分治算法(D&C算法)-CSDN博客文章浏览阅读702次,点赞9次,收藏12次。分治算法并非可用于解决问题的算法,而是一种解决问题的思路。最常见的二分查找与快速排序就是利用了分治思想。工作原理也很简单,先找出基线条件,再思考如何缩小问题的规模向基线条件靠拢,最终解决问题。
https://blog.csdn.net/a1547998353/article/details/150056606?spm=1001.2014.3001.5501
一、工作原理
对于排序算法来说,最简单的数组是什么样子的呢?就是根本不需要排序的数组。空数组或只包含一个元素的数组,在这种情况下只需要原样返回数组,根本就不用排序。
对于包含多个元素的数组,除了简单的冒泡排序和选择排序,你可以使用分治思想,尝试将数组分解,直到满足基线条件 —— 空数组或只包含一个元素的数组。
使用快速排序时,首先,需要你从数组中选择一个元素,这个元素被称为基准值。这个基准值可以是任意元素,我们一般选择数组的第一个元素用作基准值。
现在我们有一个存在三个元素的数组,选取第一个元素作为基准值。
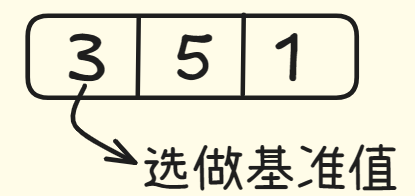
接下来,找出比基准值小的元素放在基准值一侧,比基准值大的元素放在另一侧。
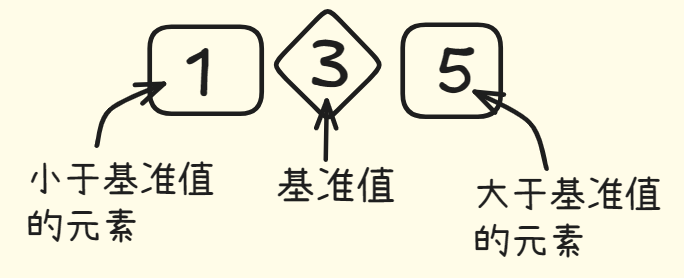
这个过程叫做分区。现在数组有三部分,一部分由所有小于基准值的数字组成的数组,一个基准值,一部分由所有大于基准值的数字组成的数组。
三个元素时,不论你选择哪个数作为基准值,分区后的两个子数组最多也只三种情况,一、只有一个元素,二、只有两个元素,三、空数组。
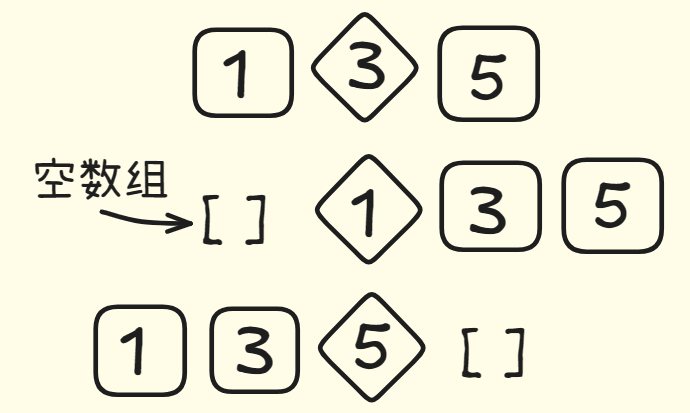
你只需要对这两个子数组再进行快速排序,合并结果就能得到一个有序数组!
当数组包含四个元素时呢。不论你选择哪个元素作为基准值,他分区后分成的两个子数组最多也只有三个元素,而你刚刚学会了如何对包含三个元素的数组排序:对其递归调用快速排序。
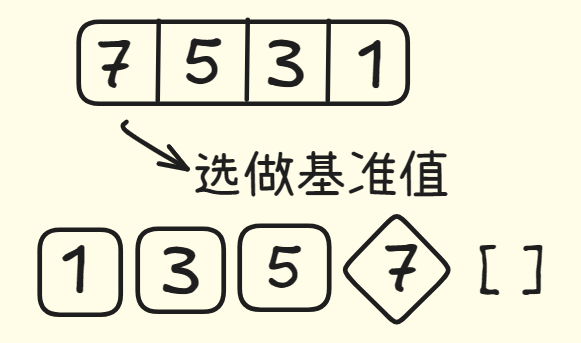
不论你选择哪个元素作为基准值,他分区后分成的两个子数组最多也只有三个元素,而你刚刚学会了如何对包含三个元素的数组排序:对其递归调用快速排序。
既然能对四个元素的数组进行快速排序了,那么你也能对五个元素的数组进行快速排序,因为五个元素时分区后子数组包含的元素都在0~4以内,以此类推,你可以对有n个数据的数组进行快速排序。
二、代码实现
#include <stdio.h>void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}// 分区操作,将数组划分为两部分,返回基准元素的索引
int partition(int arr[], int low, int high) {int pivot = arr[high]; int i = low - 1; for (int j = low; j < high; j++) {if (arr[j] <= pivot) {i++;swap(&arr[i], &arr[j]); }}swap(&arr[i + 1], &arr[high]);return i + 1;
}// 快速排序递归实现
void quickSort(int arr[], int low, int high) {if (low < high) {int pi = partition(arr, low, high);quickSort(arr, low, pi - 1);quickSort(arr, pi + 1, high);}
}// 打印数组
void printArray(int arr[], int size) {for (int i = 0; i < size; i++) {printf("%d ", arr[i]);}printf("\n");
}int main() {int arr[] = {10, 7, 8, 9, 1, 5};int n = sizeof(arr) / sizeof(arr[0]);printf("原数组: ");printArray(arr, n);quickSort(arr, 0, n - 1);printf("排序后数组: ");printArray(arr, n);return 0;
}
三、快速排序的性能
快速排序的性能高度依赖你选择的基准值。假设你总是将第一个元素用做基准值,且要处理的数组是有序的。由于快速排序算法不会检查输入的数组是否有序,因此他依然尝试进行排序。
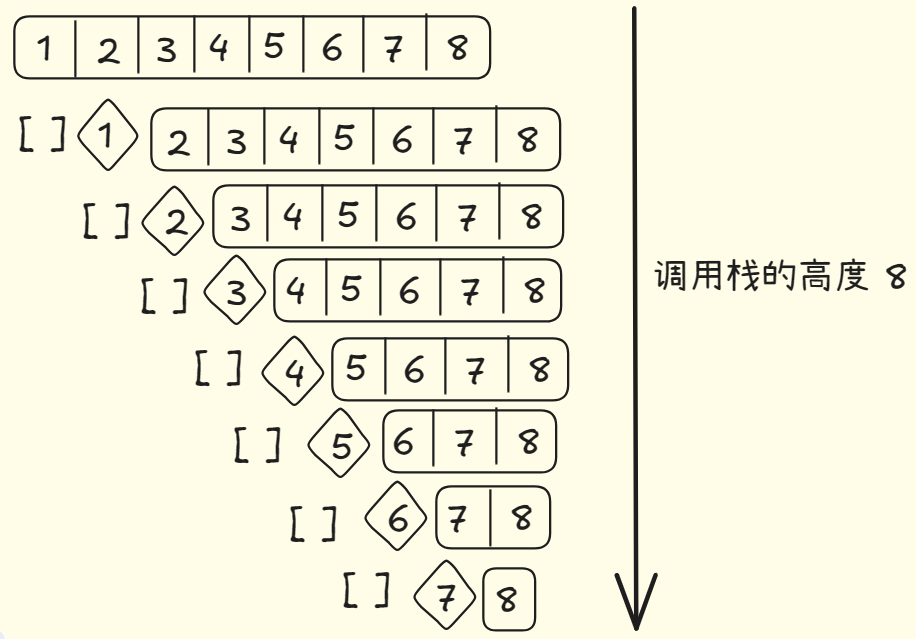
此时,数组并没有被分成两半,其中一个子数组始终为空,这导致调用栈非常长,此时栈长为 O(n)层。
假设你总是将中间值用作基准值,情况如下:
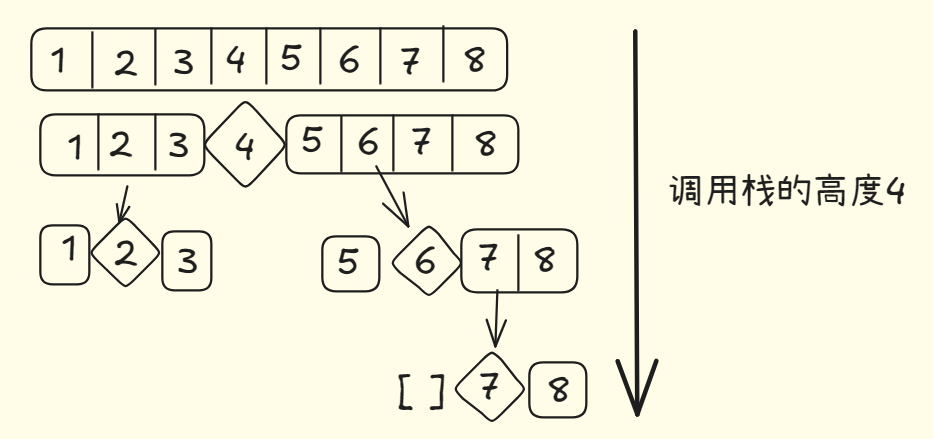
此时调用栈会短得多,因为你每次都将数组分成了两半,所以不需要那么多递归调用就能到达基线条件,此时栈长为 O(log n)层。
不论你怎么选择基准值,你都会在调用栈的每一层,使用基准值去比较每一个元素并将其划分到两个子数组中,这会涉及全部元素,因此每层的操作时间为 O(n)。整个算法所需要的时间 O = 层数 * 每层所需时间。最佳情况时有 log n 层,最糟糕时有 n 层,因此最佳情况为 O(n*log n),最糟糕时为 O(n²)。
最佳情况其实也是平均情况,只要你每次都随机的选择一个元素作为基准值,快速排序的平均时间就将为 O(n*log n)。
