范数的定义、分类与 MATLAB 应用实践
范数的定义、分类与应用
在数学分析、数值计算及工程应用中,“范数”(Norm)是一个非常重要的概念。范数可以看作是一种“度量工具”,它定义在向量空间或矩阵空间上,用于衡量元素的“大小”或“距离”,是理解空间结构和构建算法的基础。
本文将对范数的定义、常见类型及其应用进行系统性整理和介绍。
一、范数的基本定义
设 VVV 是一个向量空间,范数是一个函数 ∥⋅∥:V→R\|\cdot\| : V \to \mathbb{R}∥⋅∥:V→R,满足以下三个公理:
- 非负性(Positivity):对于任意 x∈V\mathbf{x} \in Vx∈V,有 ∥x∥≥0\|\mathbf{x}\| \geq 0∥x∥≥0,且仅当 x=0\mathbf{x} = \mathbf{0}x=0 时取等号;
- 齐次性(Homogeneity):对任意标量 α\alphaα 和向量 x∈V\mathbf{x} \in Vx∈V,有 ∥αx∥=∣α∣⋅∥x∥\|\alpha \mathbf{x}\| = |\alpha| \cdot \|\mathbf{x}\|∥αx∥=∣α∣⋅∥x∥;
- 三角不等式(Triangle Inequality):对任意 x,y∈V\mathbf{x}, \mathbf{y} \in Vx,y∈V,有 ∥x+y∥≤∥x∥+∥y∥\|\mathbf{x} + \mathbf{y}\| \leq \|\mathbf{x}\| + \|\mathbf{y}\|∥x+y∥≤∥x∥+∥y∥。
二、向量范数(Vector Norms)
向量范数用于度量向量在空间中的“长度”或“大小”。最常见的向量范数为 LpL_pLp 范数,定义如下:
∥x∥p=(∑i=1n∣xi∣p)1/p,p≥1 \|\mathbf{x}\|_p = \left( \sum_{i=1}^n |x_i|^p \right)^{1/p}, \quad p \geq 1 ∥x∥p=(i=1∑n∣xi∣p)1/p,p≥1
1. 常见的 LpL_pLp 范数类型
-
L1L_1L1 范数(曼哈顿距离):
∥x∥1=∑i=1n∣xi∣ \|\mathbf{x}\|_1 = \sum_{i=1}^n |x_i| ∥x∥1=i=1∑n∣xi∣
例如:x=(3,−4)\mathbf{x} = (3, -4)x=(3,−4),其 L1L_1L1 范数为 7。
-
L2L_2L2 范数(欧几里得范数):
∥x∥2=∑i=1nxi2 \|\mathbf{x}\|_2 = \sqrt{\sum_{i=1}^n x_i^2} ∥x∥2=i=1∑nxi2
对应于平面几何中常用的距离度量方法,如前例中 L2L_2L2 范数为 5。
-
L∞L_\inftyL∞ 范数(切比雪夫距离):
∥x∥∞=max1≤i≤n∣xi∣ \|\mathbf{x}\|_\infty = \max_{1 \le i \le n} |x_i| ∥x∥∞=1≤i≤nmax∣xi∣
例如:max(∣3∣,∣−4∣)=4\max(|3|, |-4|) = 4max(∣3∣,∣−4∣)=4。
2. 其他向量范数
-
加权范数:引入权重 wi>0w_i > 0wi>0,定义为
∥x∥w=(∑i=1nwi∣xi∣p)1/p \|\mathbf{x}\|_w = \left( \sum_{i=1}^n w_i |x_i|^p \right)^{1/p} ∥x∥w=(i=1∑nwi∣xi∣p)1/p
-
核范数(需结合核函数):用于高维映射与特征学习中。
三、矩阵范数(Matrix Norms)
矩阵范数是矩阵空间中的“度量工具”,不仅需满足基本范数公理,还需满足一致性条件:
若 A,BA, BA,B 可乘,则
∥AB∥≤∥A∥⋅∥B∥ \|AB\| \leq \|A\| \cdot \|B\| ∥AB∥≤∥A∥⋅∥B∥
1. 诱导范数(算子范数)
由向量范数引出,用于描述矩阵对向量的最大“拉伸能力”,定义为:
∥A∥p=maxx≠0∥Ax∥p∥x∥p \|A\|_p = \max_{\mathbf{x} \neq \mathbf{0}} \frac{\|A\mathbf{x}\|_p}{\|\mathbf{x}\|_p} ∥A∥p=x=0max∥x∥p∥Ax∥p
常见诱导范数包括:
-
L1L_1L1 诱导范数(列和范数):
∥A∥1=maxj∑i∣Aij∣ \|A\|_1 = \max_j \sum_i |A_{ij}| ∥A∥1=jmaxi∑∣Aij∣
-
L2L_2L2 诱导范数(谱范数):
∥A∥2=λmax(ATA) \|A\|_2 = \sqrt{\lambda_{\max}(A^T A)} ∥A∥2=λmax(ATA)
即矩阵最大奇异值,广泛用于数值计算与机器学习中。
-
L∞L_\inftyL∞ 诱导范数(行和范数):
∥A∥∞=maxi∑j∣Aij∣ \|A\|_\infty = \max_i \sum_j |A_{ij}| ∥A∥∞=imaxj∑∣Aij∣
2. 元素范数(Entrywise Norm)
直接基于矩阵元素定义:
-
Frobenius 范数(F-范数):
∥A∥F=∑i,j∣Aij∣2 \|A\|_F = \sqrt{\sum_{i,j} |A_{ij}|^2} ∥A∥F=i,j∑∣Aij∣2
可视为矩阵元素平方和的平方根,相当于向量化矩阵后的 L2L_2L2 范数。
-
核范数(nuclear norm):
∥A∥∗=∑i=1rσi \|A\|_* = \sum_{i=1}^r \sigma_i ∥A∥∗=i=1∑rσi
其中 σi\sigma_iσi 为奇异值,常用于低秩矩阵重建和稀疏优化问题。
3. Schatten 范数(奇异值范数)
Schatten 范数定义为:
∥A∥Sp=(∑i=1rσip)1/p \|A\|_{S_p} = \left( \sum_{i=1}^r \sigma_i^p \right)^{1/p} ∥A∥Sp=(i=1∑rσip)1/p
其中 p=1p = 1p=1 为核范数,p=2p = 2p=2 为Frobenius范数。
四、范数的应用领域
范数在多个学科和工程应用中发挥重要作用:
-
机器学习与正则化:
- L1L_1L1 正则化用于特征选择与稀疏模型构建(如Lasso);
- L2L_2L2 正则化用于防止过拟合(如Ridge回归)。
-
数值分析与矩阵计算:
评估矩阵条件数、控制误差传播。 -
控制理论与稳定性分析:
Lyapunov函数中使用范数评估系统状态的收敛与发散。 -
图像处理与信号压缩:
核范数用于图像重建、低秩补全等。
五、小结
范数作为度量空间中“大小”的重要工具,不仅具有清晰的数学结构,还广泛应用于各类实际问题中。掌握不同类型的范数及其性质,有助于我们从更深层次理解线性代数、优化理论和机器学习等领域的核心原理,并在实际工程中选择合适的数学工具来简化问题和提升算法性能。
六、MATLAB代码
以下是使用 MATLAB 求各种常见向量范数与矩阵范数的代码示例,便于你结合理论进行实践验证和计算分析。
✅ 一、向量范数计算
假设有向量 x = [3, -4, 1],可以使用 norm() 函数计算不同范数:
x = [3, -4, 1];% L1 范数(曼哈顿距离)
norm_L1 = norm(x, 1);% L2 范数(欧几里得范数)
norm_L2 = norm(x, 2);% L∞ 范数(切比雪夫范数)
norm_Linf = norm(x, Inf);% Lp 范数(例如 p = 3)
p = 3;
norm_Lp = norm(x, p);% 自定义加权 L2 范数(举例)
w = [0.5, 2, 1]; % 权重
norm_weighted = (sum(w .* abs(x).^2))^(1/2);
✅ 二、矩阵范数计算
假设有矩阵:
A = [1, -2, 3; 4, 0, -1];
1. 诱导范数(基于 norm 函数)
% L1 范数(列和最大值)
norm_A1 = norm(A, 1);% L2 范数(谱范数 / 最大奇异值)
norm_A2 = norm(A, 2);% L∞ 范数(行和最大值)
norm_Ainf = norm(A, Inf);
2. Frobenius 范数
% Frobenius 范数
norm_F = norm(A, 'fro');
3. 核范数(nuclear norm)
% 核范数(奇异值之和)
s = svd(A);
norm_nuclear = sum(s);
4. Schatten p-范数(p = 3 示例)
p = 3;
s = svd(A);
norm_Schatten = (sum(s.^p))^(1/p);
✅ 三、条件数计算(衍生应用)
范数在矩阵条件数计算中也很常见:
% A 的条件数(默认使用 2-范数)
cond_A = cond(A);% A 的1-范数条件数
cond_A1 = cond(A, 1);% A 的∞-范数条件数
cond_Ainf = cond(A, Inf);
✅ 四、小结
| 名称 | MATLAB命令 | 备注说明 |
|---|---|---|
| 向量 L1 范数 | norm(x,1) | 元素绝对值之和 |
| 向量 L2 范数 | norm(x,2) 或 norm(x) | 向量欧氏范数 |
| 向量 L∞ 范数 | norm(x,Inf) | 元素绝对值最大值 |
| 矩阵 L1 范数 | norm(A,1) | 列绝对值和的最大值 |
| 矩阵 L2 范数 | norm(A,2) | 最大奇异值(谱范数) |
| 矩阵 L∞ 范数 | norm(A,Inf) | 行绝对值和的最大值 |
| Frobenius 范数 | norm(A,'fro') | 所有元素平方和开根号 |
| 核范数 | sum(svd(A)) | 奇异值之和 |
| Schatten-p 范数 | sum(svd(A).^p)^(1/p) | 奇异值的 LpL_pLp 范数 |
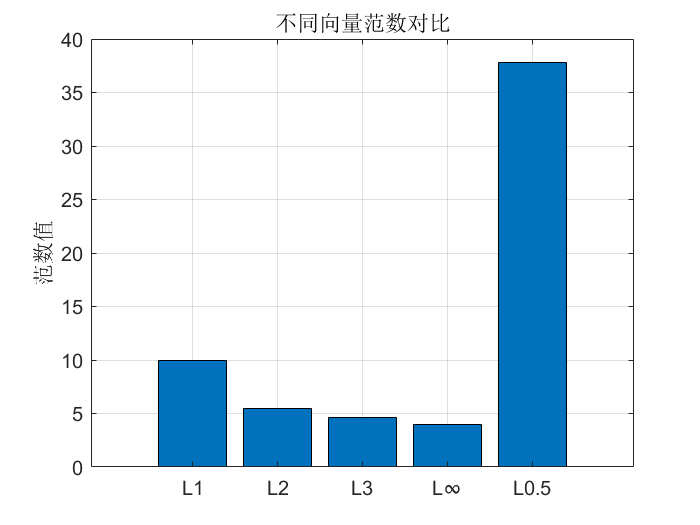
向量范数对比
% 示例向量
x = [3, -4, 1, 2];% 范数计算
norm_L1 = norm(x, 1);
norm_L2 = norm(x, 2);
norm_Linf = norm(x, Inf);
norm_L3 = norm(x, 3);
norm_L0p5 = sum(abs(x).^0.5)^(1/0.5); % L_0.5 伪范数(非真正范数)% 汇总数据
norm_values = [norm_L1, norm_L2, norm_L3, norm_Linf, norm_L0p5];
norm_labels = {'L1', 'L2', 'L3', 'L∞', 'L0.5'};% 绘图
figure;
bar(norm_values);
set(gca, 'XTickLabel', norm_labels, 'FontSize', 12);
ylabel('范数值');
title('不同向量范数对比');
grid on;
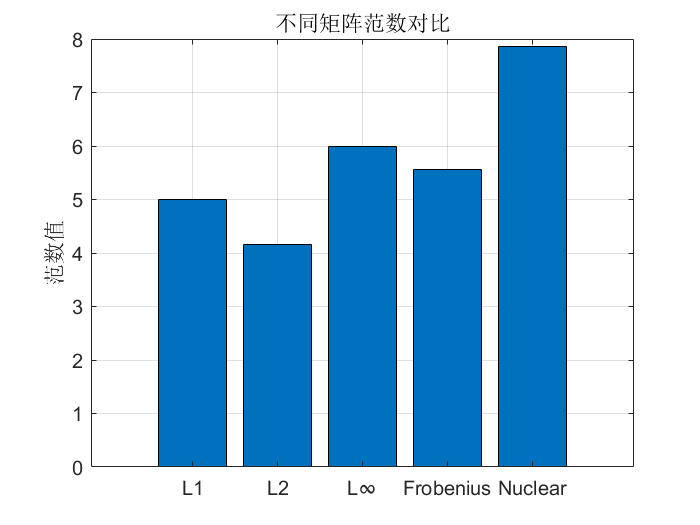
矩阵范数对比
A = [1, -2, 3; 4, 0, -1];
norms = [norm(A,1), norm(A,2), norm(A,Inf), norm(A,'fro'), sum(svd(A))];
labels = {'L1', 'L2', 'L∞', 'Frobenius', 'Nuclear'};figure;
bar(norms);
set(gca, 'XTickLabel', labels, 'FontSize', 12);
ylabel('范数值');
title('不同矩阵范数对比');
grid on;