【dp】最长递增子序列
文章目录
- 方法一:动态规划
- 方法二:贪心 + 二分查找
- 构造最长递增子序列

方法一:动态规划
- dp[i]:末尾元素为arr[i]的最长子序列的长度
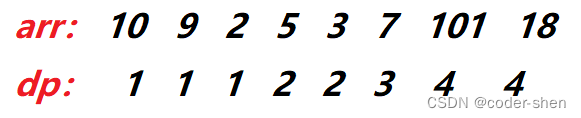
从0遍历到i - 1,若遍历到的元素小于当前值arr[i],表示当前值arr[i]可以和前面的某个值组成递增序列,则尝试更新dp[i]
int LIS(vector<int>& arr) {int n = arr.size();if(n == 0) return 0;vector<int> dp(n, 1);int ans = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(arr[j] < arr[i]){dp[i] = max(dp[i], dp[j] + 1);}}ans = max(ans, dp[i]);}return ans;
}
时间复杂度: O ( N 2 ) O(N^2) O(N2)
方法二:贪心 + 二分查找
我们考虑维护一个数组 min_tails,min_tails[i]表示长度为i + 1的递增子序列末尾元素的最小值,min_tails并不是记录arr中的递增子序列

看最后一个g数组,g[2]=3,表示长度为3的递增子序列末尾的最小值为3。长度为3的递增子序列有[1,6,7]、[1,2,4]、[1,2,5]、[1,2,3]
为什么min_tails数组中要维护各个不同长度递增子序列末尾元素的最小值呢?
min_tails数组中维护各个不同长度递增子序列末尾元素的最小值时,arr的后续元素可以和不同长度子序列末尾的最小值比较,从而确定后续元素可以加入哪个子序列,成为新的递增子序列

int LIS(vector<int>& arr) {int n = arr.size();if(n == 0) return 0;vector<int> tails(n);min_tails[0] = arr[0];int len = 1;for(int i = 1; i < n; i++){// 如果当前元素比长度为len的子序列末尾元素的最小值大,说明当前元素可以和长度为len的子序列组成新的递增子序列if(min_tails[len - 1] < arr[i]){min_tails[len] = arr[i];len++;continue;}// 二分:用arr[i]更新tails中最靠左侧的大于arr[i]的值int l = 0;int r = len;while(l < r){int mid = l + (r - l) / 2;if(min_tails[mid] < arr[i]) l = mid + 1; // 用l找第一个比arr[i]大的值,也可以找最后一个小于等于arr[i]的值else r = mid;}min_tails[l] = arr[i];}return len;
}
构造最长递增子序列
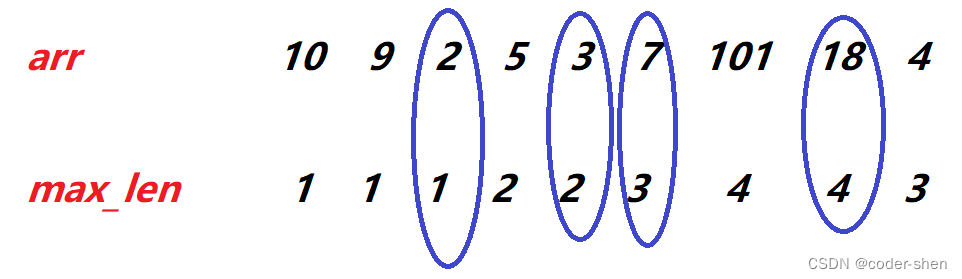
max_len相同时取最小的,ans初始化为len个元素,从后往前填写。如果max_len相同,靠后的arr[i]一定更小,若靠后的arr[i]更大,那max_len就不能相同了。比如:
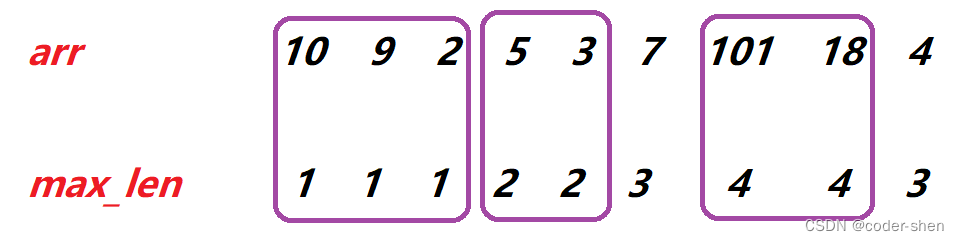
class Solution {
public:vector<int> LIS(vector<int>& arr) {int n = arr.size();if(n < 2) return arr;vector<int> min_tails(n); // min_tails[i]:长度为i+1的最长递增子序列末尾元素的最小值min_tails[0] = arr[0];int len = 1; // 当前最长递增子序列的长度vector<int> max_len(n); // max_len[i]:表示以arr[i]结尾的最长递增子序列的长度max_len[0] = 1;for(int i = 1; i < n; i++){// 当前元素arr[i]已经比当前最长递增子序列末尾元素的最小值要大,说明可以和当前递增子序列组成新的递增子序列if(arr[i] > min_tails[len - 1]){min_tails[len] = arr[i];max_len[i] = len + 1; // arr[i]可以增加最长递增子序列的长度len++;continue;}// arr[i]不能和当前最长递增子序列组成新的递增子序列,可以尝试用arr[i]和较短的递增子序列组成新的递增子序列(极端情况下,arr[i]自己组成长度为1的递增子序列)// 在[l, r)之间找第一个大于arr[i]的位置,说明arr[i]可以和前面较短的递增子序列组成新的递增子序列,用arr[i]更新第一个大于arr[i]的元素,即让某递增子序列的长度不变,而末尾元素变小int l = 0;int r = len;while(l < r){int mid = l + (r - l) / 2;if(min_tails[mid] < arr[i]) l = mid + 1;else r = mid; // 不能是r = mid - 1,因为要找第一个大于arr[i]的值,此时min_tails[mid] >= arr[i],r = mid - 1会跳过大于arr[i]的min_tails[mid]}min_tails[l] = arr[i];max_len[i] = l + 1; // arr[i]不能增加最长递增子序列的长度,min_tails[l]是第一个大于arr[i]的元素,即用arr[i]可以组成长度为l + 1的递增子序列}vector<int> ans(len);int idx = len - 1;// 只能按顺序填for(int i = n - 1; i >= 0; i--){// 遍历max_len数组,最大长度为idx + 1时才可填写ans[idx],max_len相同时必然取最靠后的arr[i],因为最靠后的最小if(max_len[i] == idx + 1){ans[idx] = arr[i];idx--;}}return ans;}
};
