当前位置：首页 > news >正文

Pytorch-05 所以计算图和自动微分到底是什么？（计算图及自动微分引擎原理讲解）

news 2025/8/5 12:51:57

所以计算图和自动微分到底是什么？

相信大家一定在学习反向传播的时候听到过这两词，但说实话，我一直没太搞懂这两玩意到底到底是怎么在pytorch中实现的，刚好pytorch教程也到这里了，所以打算挑战一下自己，把这两个最有难度的概念试着讲讲。

本篇文章主要讲解了pytorch自动微分机制中如下几个重要概念：

反向传播
torch.autograd.Function机制
计算图机制
如何使用计算图算出梯度
如何停止梯度追踪

当训练神经网络的时候，我们需要通过损失函数相对于需要学习参数的梯度来调整模型的权重。

为了计算这些梯度，我们需要反向传播算法，其会在一次minibatch的前向传播之后，链式的，一次性的把所有要学习的权重对于Loss的梯度一次性全部算出来
在这里插入图片描述
这个计算的手法叫做 以计算图实现的自动微分，由pytorch内置的 自动微分引擎，torch.autograd 所实现。

在pytorch中，当一个网络的结构被__init__，亦或者一个级联的计算过程被定义后，pytorch会自动生成其计算图。下面我们用一个简单的单层神经网络进行计算图和自动微分的原理讲解。

1. 定义一个网络结构

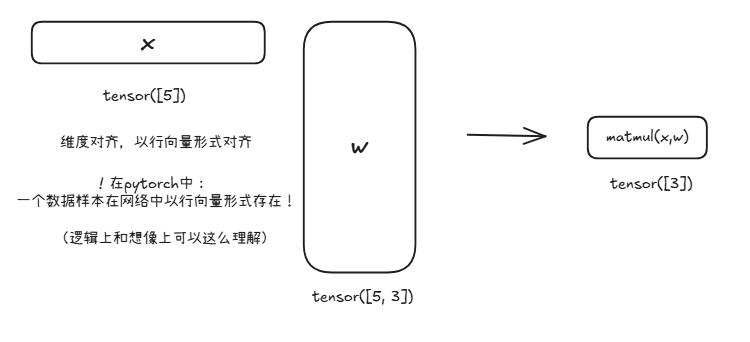
让我们做一个简单的单层神经网络出来，其接受一个长度为5的1D tensorx，一个尺寸为5x3的矩阵w，以及一个长度为3的1D 偏置 b

import torchx = torch.ones(5)
y = torch.zeros(3)
w = torch.randn(5, 3, requires_grad=True)
b = torch = randn(3, requires_grade=True)
z = torch.matmul(x, w) + b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

你可能对这里面的matmul(x, w)感觉有点奇怪，这感觉也许和之前线性代数学到的矩阵在左，向量在右的乘法不太一样，这是因为在torch中，一般情况下一个数据样本以行向量形式存在，所以这样乘才是比较符合语义信息的。

在这里插入图片描述
还有一个比较疑惑的点就是你可能不知道这里的requires_grade是什么意思，这个我们后面会详细说。

2. 节点，Functions 和计算图

逻辑上，刚才定义好的网络的计算流程可以可视化成这样：
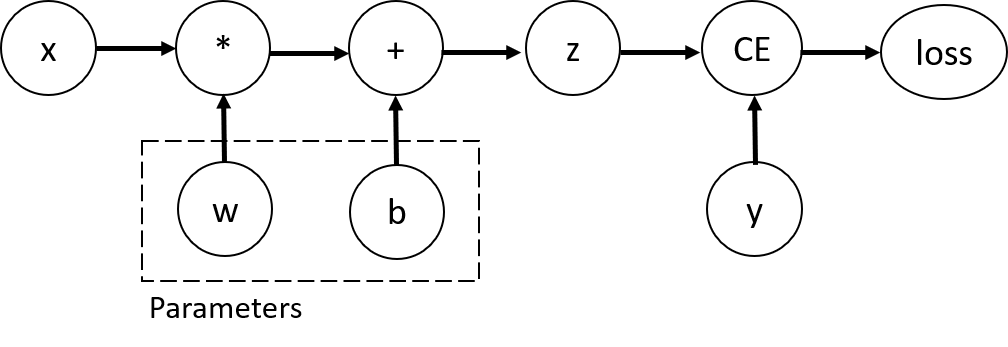
在这里插入图片描述
每一个节点可以代表Tensor数据，或者操作。以上就是一个单层线性层网络+交叉熵损失计算的完整计算图。在这个网络中，w和b是网络要学习的参数。因此，我们需要在反向传播的时候计算并保存它两对loss贡献的梯度，然后再使用优化器根据梯度来调整参数。 这可以通过设置tensor的require_grad=True属性来实现。

不设置require_grad=True的参数/节点的梯度将不会被保存！

你可以在创建的时候就指定requires_grad=True，也可以之后再使用x.requires_grad_(True)方法来重新开启其保存LOSS梯度的功能。

逻辑上的计算图可以通过画图很好地构造出来，但是代码实际运行的时候，计算图是以什么样的方式存在呢？

在 PyTorch 的世界里，计算图并不是一个预先画好的蓝图，而是在代码执行时动态构建的。这个过程的核心思想可以这样理解：

原子操作的包装：Function 类
PyTorch 中的每一个基本操作，比如矩阵相乘、加法或 ReLU 激活，都被封装成一个特殊的Function 类，这个类会有两个关键方法：
- 前向（Forward）：它知道如何执行操作，根据输入张量计算出新的输出张量。
- 反向（Backward）：它也内置了如何根据链式法则计算梯度的逻辑。
  
  以上就是一个Exp操作类的样子。
动态链接：grad_fn 属性
当你执行一个操作时，PyTorch 会自动做两件事：
- 生成新的张量：根据forward函数计算出操作的结果。
- 创建回溯链：将这个新的张量与产生它的那个 Function 类的实例（我们称之为 grad_fn）关联起来。
grad_fn 就像一张 “追溯标签”，贴在新生成的张量上。它记录了“我是由哪个操作产生的”，以及“如果需要反向传播，请来找我的backward函数”。
隐式存在：计算图的本质
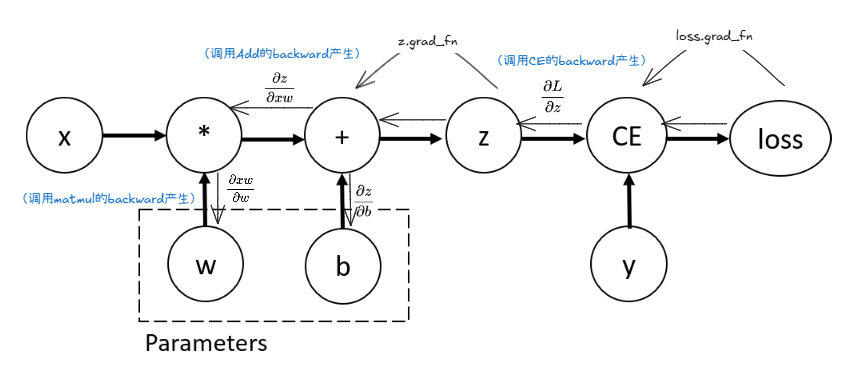
因此，PyTorch 的计算图并非一个集中的数据结构，而是一条由张量和它们的 grad_fn 属性串成的“链条”。这条链从最初的输入张量（叶子节点）开始，一直延伸到最终的输出张量（根节点，通常是损失）。

3. 反向传播：链式法则的应用

loss.backward()
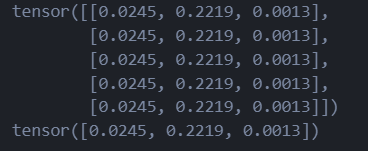
print(w.grad)
print(b.grad)

当你调用 loss.backward() 时，PyTorch 就会从 loss 张量开始，顺着它身上的 grad_fn 标签，一步步地向后追溯这条链。它会在每一步调用对应 grad_fn 内置的反向传播逻辑，将梯度从后向前传递（传递的时候进行连乘），直到计算出需要计算梯度的学习节点（例如 w 和 b）的梯度，并将其保存在 .grad 属性中。（这里直接保存的是相对于Loss的梯度了！ $∂L∂w\frac{\partial L}{\partial w}$ $∂L∂b\frac{\partial L}{\partial b}$ 这种）

在这里插入图片描述

注意，每一个节点调用自己的grad_fn之后，只会算出局部梯度，也就是自己相对与上一节点的梯度，并且没有使用required_grad=True的节点是不会保存自己相对于Loss的梯度的，它们的梯度只会作为中间变量传递给之前的节点，以供之前的节点算出自身相对于Loss的梯度！

在我们的例子里面，试着调用访问z.grad_fn 和loss.grad_fn:

print(f"Gradient function for z = {z.grad_fn}")
print(f"Gradient function for loss = {loss.grad_fn}")

在这里插入图片描述

可以看到它们都之指向了上一步产生它们的函数对象，调用调用该函数对象的backward函数可以直接获得局部梯度，以供链式求导计算需要学习参数的梯度。
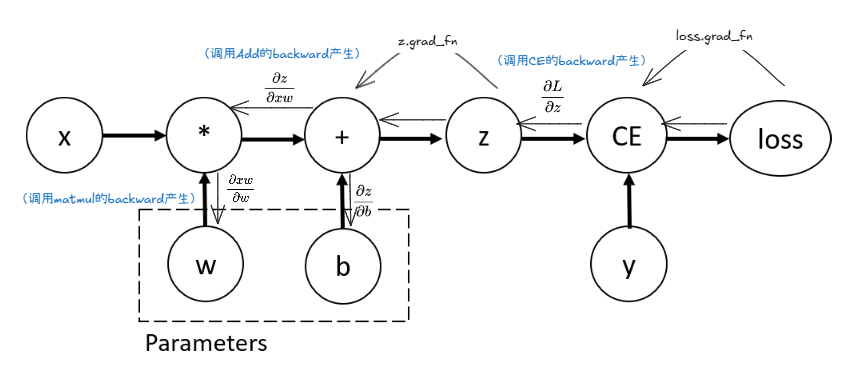
在这里插入图片描述

图中每一个梯度的计算表达式，都已经被编码到backward函数中，根据前向传播的值就可以计算出来当前的局部梯度了。一下是+操作的backward伪代码

这种“动态、分布式”的思想正是pytorch的核心设计思想，这也是其与tensorflow的最大不同之一。它让 PyTorch 的自动求导机制既高效又极具灵活性。

4. 关闭梯度追踪

训练情况下，所有开启了requires_grad=True的tensors都会保存自己相对于Loss的梯度。但是，推理情况下，因为只需要用到前向传播，所以就没有必要使用梯度了。这种时候，就可以使用torch.no_grad()块，将之前设置过require_grad=True的tensors重新设置为False，停止对参数的梯度记录。

z = torch.matmul(x, w)+b
print(z.requires_grad)with torch.no_grad():z = torch.matmul(x, w)+b
print(z.requires_grad)

在这里插入图片描述

还有一种情况你可能会需要停止梯度追踪，那就是你想冻结网络某些部分的参数的时候，这个比较高阶，之后再说。

5. 更多关于计算图的内情

从逻辑概念上讲，autograd 在一个由 Function 对象组成的有向无环图（DAG） 中（但是实际上代码中没有这个数据结构啊，这个DAG是由节点直接通过grad_fn相连在逻辑上形成的），记录了数据（张量）和所有已执行的操作（以及产生出的新张量）。在这个 DAG 中，叶子是输入张量，根是输出张量。通过从根追溯到叶子，你可以使用链式法则自动计算梯度。

在前向传播中，autograd 同时做两件事：