当前位置：首页 > news >正文

15.2 矩阵链乘法

news 2025/9/11 8:05:07

1.代码

public class MatrixChainMultiplication {public static void main(String[] args) {
//        在该代码中，我们首先创建了两个n * n的矩阵m和s，分别用于记录最优值和分割点。 其中m 矩阵 通过i j 来显示在i到j的矩阵链中最优解
//
//        然后，我们将i = j时的m[i][j]赋值为0，因为一个矩阵的乘积为0。
//
//        接下来，我们使用L循环枚举子问题规模，i循环枚举左端点，j循环枚举右端点，并使用k循环枚举分割点。
//
//        对于每个分割点k，我们计算最优值q，然后将q与m[i][j]进行比较，如果q小于m[i][j]，则更新m[i][j]和s[i][j]。
//        通过公式算法导论15.7
//
//        最后，我们返回m[1][n-1]，即原问题的最优值。
//
//        该算法的时间复杂度为O(n^3)，其中n是矩阵的数量。int[] p = {30, 35, 15, 5, 10, 20, 25};System.out.println("最少的乘法次数为：" + matrixChainOrder(p));}
public static int matrixChainOrder(int[] p) {int n = p.length;// 创建n * n的矩阵m和s，用于记录最优值和分割点int[][] m = new int[n][n];int[][] s = new int[n][n];// i==j时，m[i][j]=0，因为一个矩阵的乘积为0for (int i = 1; i < n; i++) {m[i][i] = 0;}for (int i = 0; i < m.length; i++) {System.out.println(Arrays.toString(m[i]));}
// L是子问题规模for (int L = 2; L < n; L++) {// i是左端点，j是右端点，k是分割点for (int i = 1; i < n - L + 1; i++) {int j = i + L - 1;m[i][j] = Integer.MAX_VALUE;// 枚举分割点k，求解最优值for (int k = i; k < j; k++) {int q = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];System.out.println("m[i][k]: "+m[i][k] );System.out.println("m[k + 1][j]: "+m[k + 1][j]);System.out.println("i:"+i+" k:"+k+" j:"+j);System.out.println(q);if (q < m[i][j]) {m[i][j] = q;s[i][j] = k;}}}}// 返回最优值return m[1][n - 1];}


}

2.原理

自己看算法导论吧

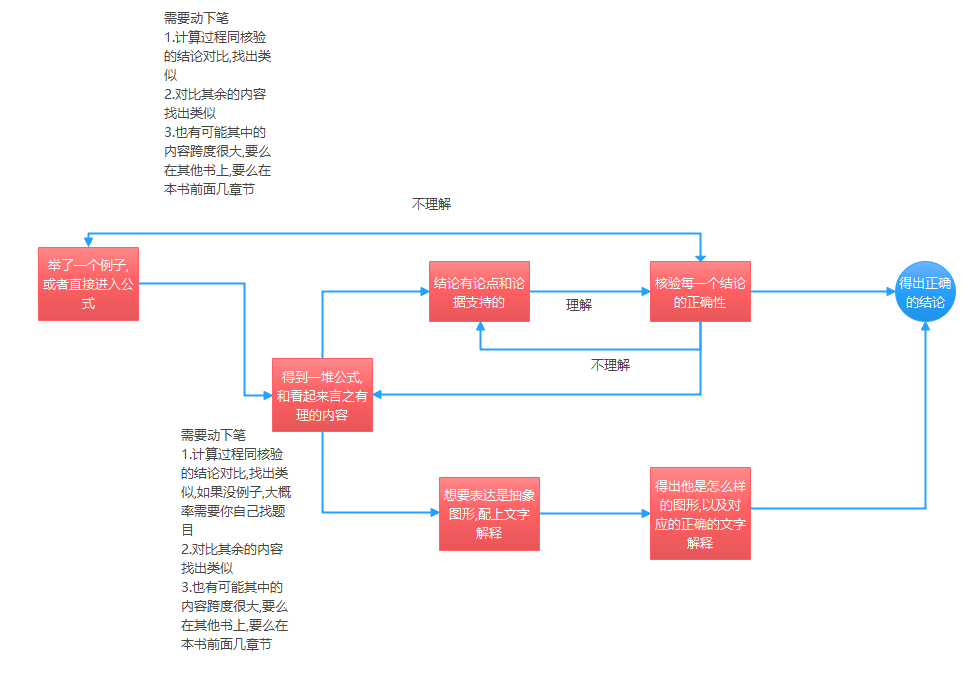
我再看到

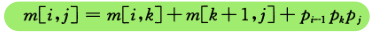
这条公式的时候很困惑,然后自己手算了他给的第一个例子才知道这是正确的.

3.问题

具体的问题已经在代码注释中讲解完毕

4.进阶

输出只是I一个普通的递归而已

package collection;

public class printOptimalParens {public static void matrixChainOrder(int[] p) {int n = p.length - 1;int[][] m = new int[n + 1][n + 1];int[][] s = new int[n + 1][n + 1];for (int i = 1; i <= n; i++) {m[i][i] = 0;}for (int len = 2; len <= n; len++) {for (int i = 1; i <= n - len + 1; i++) {int j = i + len - 1;m[i][j] = Integer.MAX_VALUE;for (int k = i; k <= j - 1; k++) {int q = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];if (q < m[i][j]) {m[i][j] = q;s[i][j] = k;}}}}System.out.println("Optimal Parenthesization:");printOptimalParens(s, 1, n);}
public static void printOptimalParens(int[][] s, int i, int j) {if (i == j) {System.out.print("A" + i);} else {System.out.print("(");printOptimalParens(s, i, s[i][j]);printOptimalParens(s, s[i][j] + 1, j);System.out.print(")");}}
public static void main(String[] args) {int[] p = {30, 35, 15, 5, 10, 20, 25};matrixChainOrder(p);}
}