交互 Codeforces Round 1040 Interactive RBS
题目大意:
交互题。有一个隐藏的括号序列,只由 "(" 和 ")" 组成,保证至少有一个"(" 和一个 ")"。
你需要通过若干次查询猜出这个确定的序列。

Easy Version:最多查询 550 次
Medium Version:最多查询 200 次
Hard Version:最多查询 200 次
Solution:
Easy Version
查询次数限制提示我们一次查询要找到两个元素。
首先我们可以通过二分找到一般情况下第一个 “()” 出现的位置,特例是形如 "))))).....(((((" 的序列。
那么对于一般情况,二分一个mid,查询 [1,mid] 这个连续的子序列,如果查询值不为 0,说明这段序列中存在 “()” 。
于是无论哪种情况,我们都可以找到一个 "(" 和一个 ")" 所在的位置(特例就是 n 和 1 )。
然后我们需要构造一个查询方式,每次查询两个位置,如果这两个位置的不同排列组合情况对应不同的查询值,我们就可以确定地判断这两个位置的元素是什么,官解构造方式如下:
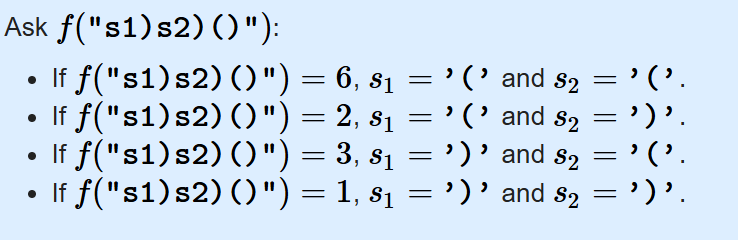
Code:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;#define N 1005int T,n,a[N],pl,pr,ans[N];void solve(int x,int y)
{int num;printf("? 6 %d %d %d %d %d %d\n",x,pr,y,pr,pl,pr);cout.flush();scanf("%d",&num);if(num == 1) ans[x] = ans[y] = 2;if(num == 2) ans[x] = 1,ans[y] = 2;if(num == 3) ans[x] = 2,ans[y] = 1;if(num == 6) ans[x] = ans[y] = 1;return;
}int main()
{scanf("%d",&T);while(T --){memset(ans,0,sizeof ans);scanf("%d",&n);int l,r,mid,x,tmp;l = 2,r = n,tmp = 0;while (l <= r){mid = (l + r) >> 1;printf("? %d ",mid);for (int i = 1;i <= mid;++ i)printf("%d ",i);printf("\n");cout.flush();scanf("%d",&x);if(x) tmp = mid,r = mid - 1;else l = mid + 1;}if(!tmp) pl = n,pr = 1;else pl = tmp - 1,pr = tmp;for (int i = 1;i <= n - 1;i += 2) solve(i,i + 1);if(!ans[n]) solve(n - 1,n);printf("! ");for (int i = 1;i <= n;++ i)if(ans[i] == 1) printf("(");else printf(")");printf("\n");cout.flush();}return 0;
}Medium Version
官解用的是状压的思想,往二进制方向想,也是十分巧妙。

Hard Version
思考我们一次能否查询更多的位置呢?
先观察到一个小性质:在两个合法括号序列中间随便插一个 ")" 就能把这两个合法序列的贡献分开
例如:
()()() 查询值是 6
()())() 查询值是 3 + 1 = 4
构造这样的查询序列:
"s1))s2)s2))s3)s3)s3))s4)s4)s4)s4)s4))......s12))"
当且仅当si == '(' 的时候,它负责的那一段括号序列才有贡献,并且贡献 = gi * (gi + 1) / 2,其中 gi 是第 i 段的 "si)" pairs 的数目。
那么只需满足:
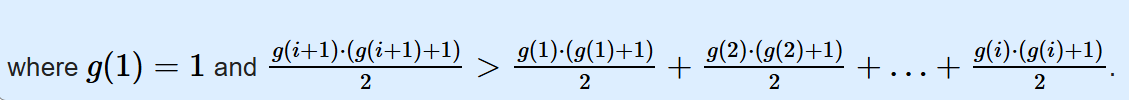
即可对每一段贡献拆开判断。
这里其实用到的是类似 2^n > 2^(n-1) + ... + 2^1 + 2^0 的思想,这样我们从高位到低位一个个判断,如果 查询值 > gi * (gi + 1) / 2,说明第i段有贡献,si == '(',然后把查询值减掉这段的贡献接着判断下去就可以了。
事实上,根据题目“每次查询的序列长度 k <= 1000” 可以知道,我们一次最多能查询13个位置,但是每次查12个也足够通过 hard version 的限制了,每次13个的原理也是一模一样。
最后要注意的是我们是12个12个的查,最后剩下的未知括号位置少于12的时候,需要特殊处理。(可以直接用easy version的方法把最后几个剩余的位置判断了,简单计算一下这样最多查询次数刚好90多,不到100)
Code:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;#define N 1005int T,n,a[N],pl,pr,res,ans[N],g[20],f[20];void preprocess()
{g[1] = f[1] = res = 1;int now = 1;int sum = 1;for (int i = 2;i <= 12;++ i){while (now * (now + 1) / 2 <= sum) ++ now;g[i] = now;f[i] = now * (now + 1) / 2;sum += f[i];res += g[i];}res = res * 2 + 12;return;
}void print(int tot,int pos)
{for (int i = 1;i <= tot;++ i)printf("%d %d ",pos,pr);printf("%d ",pr);return;
}void solve(int x,int y)
{printf("? %d ",res);for (int i = x;i <= y;++ i){int id = i - x + 1;print(g[id],i);}printf("\n");cout.flush();int num;scanf("%d",&num);for (int i = y;i >= x;-- i){int id = i - x + 1;if(num >= f[id]) num -= f[id],ans[i] = 1;else ans[i] = 2;}return;
}void sol(int x,int y)
{int num;printf("? 6 %d %d %d %d %d %d\n",x,pr,y,pr,pl,pr);cout.flush();scanf("%d",&num);if(num == 1) ans[x] = ans[y] = 2;if(num == 2) ans[x] = 1,ans[y] = 2;if(num == 3) ans[x] = 2,ans[y] = 1;if(num == 6) ans[x] = ans[y] = 1;return;
}int main()
{preprocess();scanf("%d",&T);while (T --){memset(ans,0,sizeof ans);scanf("%d",&n);int l,r,mid,x,tmp;l = 2,r = n,tmp = 0;while (l <= r){mid = (l + r) >> 1;printf("? %d ",mid);for (int i = 1;i <= mid;++ i)printf("%d ",i);printf("\n");cout.flush();scanf("%d",&x);if(x) tmp = mid,r = mid - 1;else l = mid + 1;}if(!tmp) pl = n,pr = 1;else pl = tmp - 1,pr = tmp;int now = 0;for (int i = 1;i + 11 <= n;i += 12)solve(i,i + 11),now = i + 11;if(now < n){for (int i = now + 1;i <= n - 1;i += 2) sol(i,i + 1);if(!ans[n]) sol(n - 1,n);}printf("! ");for (int i = 1;i <= n;++ i)if(ans[i] == 1) printf("(");else printf(")");printf("\n");cout.flush();}return 0;
}一道非常巧妙的构造序列交互题^^
