zset 中特殊的操作

首先 zset 与我们常规的 redis 操作有所不同, 这里的时间复杂度基本都是 O(log N) 起步的

目录

1. zcount 

2. zpopmax

---

1. zcount 

zcount key min max : 这里求的是 key 中下标在 min 和 max 之间的 元素的数量, 这里是比区间

我们要是想排除端点, 就需要加上 ( , 无论是左端点还是右端点都是要加上 (

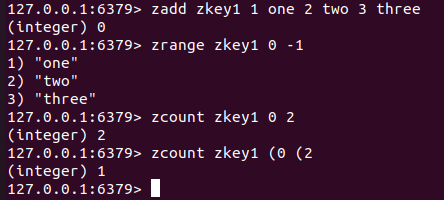
为什么要这样设计呢? 

是因为在开发的时候就已经这样设定了, 只能去蹲守这样的规则~~  后面要是想改过来, 是很难的, 这是因为兼容性的原因, 广泛使用的软件, 一旦在新的版本中, 引入和之前不兼容的特性, 成本是非常高的

时间复杂度 : O(log N)

zcount 指定 min 和 max 分数区间的 ~~

先根据 min 找到对应的元素, 在根据 max 找到对应的元素 (log (N))

在上面找到一个的情况下, 如果进行一个遍历, 是不是就知道这里元素的个数了呢? 如果区间中的元素比较多, 此时要进行遍历, 复杂度就成了 O(log (N) + M), M市区件中元素的个数, N 使整个有序集合的元素个数 (错误的方法)

实际上, zset 内部会记录每个元素当前的 "排行" / "次序", 查询到两个元素, 直接就知道了元素所在的 "次序", 就可以直接把 max 对应的元素次序和 min 对应的元素次序, 减法即可

min 和 max 是可以写成浮点数(zset分数本身就是浮点数)

在浮点数中，存在两个特殊的数值: 

        inf : 无穷大

        -inf : 负无穷大 (不是无穷小)

2. zpopmax

zpopmax key count : 对 key 进行尾删 count 个

如果存在多个元素, 分数相同, 同时为最大值, zpopmax删的时候, 仍然只删除其中一个元素 (字典排序)

时间复杂度 : (log (N) * M) , M : 要删除的元素个数

既然是尾删, 为什么我们不把这个最后一个元素的位置特殊记录下来, 后续山粗不就可以 O(1) 了吗? 省去了查找的过程.

但是很遗憾, 目前 redis 并没有这么做, 事实上, redis 的源码中, 针对有序集合, 确实是记录了尾部这样特定的位置~~, 但是在实际删除的时候, 并没有用上这个特性, 而是直接调用了一个 "通用的删除函数" (给定一个 member 的值, 进行查找找到位置之后再删除~~) (这里应该是可以进行优化的)