逻辑回归----银行贷款模型优化

信用卡交易数据有个特点——欺诈交易（Class=1）极少，通常只占 0.1% 左右。
用极度不平衡的数据直接训练模型，会出现一个尴尬局面：

• 模型只要把所有人都预测成“正常（Class=0）”，准确率就能高达 99.9%。

• 但我们要抓的“欺诈”却全军覆没——这在金融场景里是不能接受的。

 一、评价模型：

1.混淆矩阵 ：

在完成模型训练与参数调优之后，仅凭整体准确率（accuracy）难以充分刻画分类器在高度不平衡数据上的真实表现。尤其在欺诈检测等高风险业务场景中，更为关键的是对“欺诈样本被正确识别”以及“正常样本被误报”两类错误的定量刻画。混淆矩阵（confusion matrix）通过将预测结果与实际标签进行交叉汇总，为上述问题提供了直观、可解释的诊断框架。

混淆矩阵基本形式：

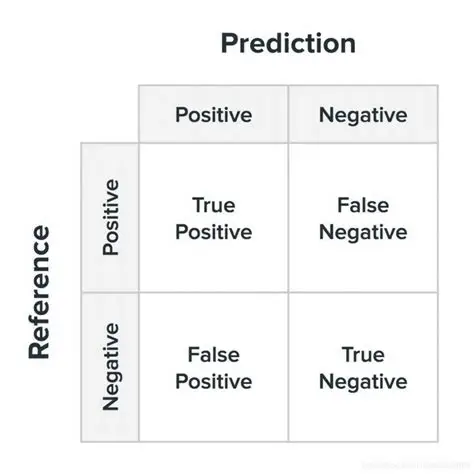
• TP（真正例）：模型正确识别出的欺诈交易数量。

• FN（假负例）：实际为欺诈却被模型误判为正常的交易数量。

• FP（假正例）：实际为正常却被模型误判为欺诈的交易数量。

• TN（真负例）：模型正确识别出的正常交易数量。

 Accuracy(准确率)：

accuracy = (TP+TN)/(TP+TN+FP+FN)

Precision(精确率)：

precisio = TP/(TP+FP)

Recall(召回率)：

recall = TP/(TP+FN)

银行真正重视的数据（真实值=1的召回率），宁可错杀绝不放过。

F1-score(F1值)：

F1 = 2*(precision*recall)/(precision+recall)

一种综合数据，不注重召回率时，f1就会更为重要。

2.正则化惩罚：

正则化惩罚（Regularization Penalty）是机器学习中用于防止模型过拟合（Overfitting）的核心技术之一，通过在损失函数中引入额外的约束项，限制模型参数的复杂度，从而提升泛化能力

均方差损失函数：loss = (1/n) * Σ(yᵢ - y)²+ λ·R(w)

目标求loss整体式子的极小值

例：输入为x = [1,1,1,1]

                 w1=[1,0,0,0]

                 w2 = [0.25,0.25,0.25,0.25]

w1和w2与带入输入值，都等于1，但明显可以看出，w1仅仅与第一个输入信息有关而w2与每一个输入数据都有关，w1相较于w2数据较为极端。

有两种常见的正则化表示：

1. L2 正则化

加入 L2 正则化的均方差损失函数为：

L2= λ·(Σwⱼ²)

L2 正则化的惩罚项是权重参数的平方和，它会鼓励权重值都趋向于较小的数值，但不会使它们变为 0。这种特性使得模型能保留所有特征的影响，只是每个特征的影响都不会过大。

2. L1 正则化

加入 L1 正则化的均方差损失函数为：

L1=λ·(Σ|wⱼ|)

L1 正则化的惩罚项是权重参数的绝对值之和，它会促使部分权重变为 0，相当于自动完成了特征选择过程。在特征数量较多的情况下，Lasso 回归可以帮助我们找到最具预测能力的少数特征。

一般选择L2惩罚项。

当 w的值越极端时，会惩罚权重w，L的值越大，loss的值也就越大，与目标不符。

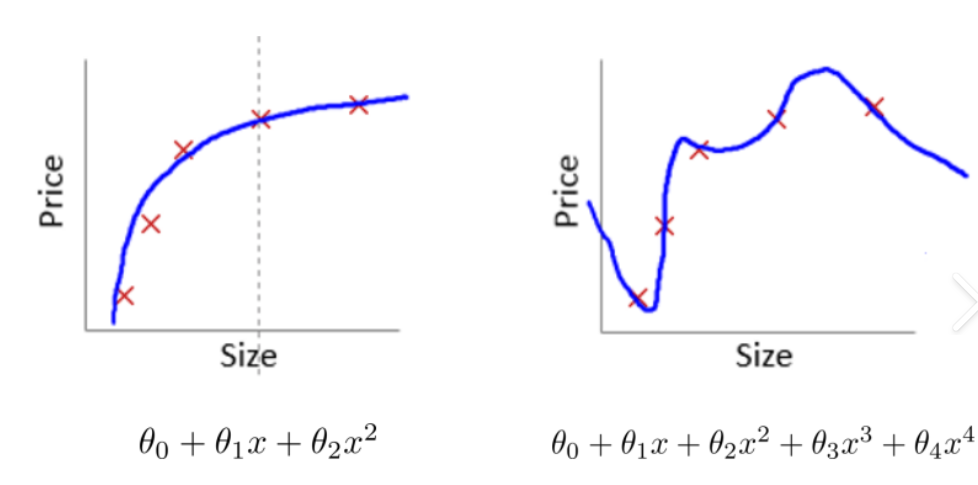
正则化惩罚的目的：

• 核心目标：防止模型过拟合
• 表现特征：训练时自测正确率很高，但测试时正确率骤降
• 理想状态：训练正确率100%时，测试正确率应保持在92%-95%区间

 λ如何选择：

 λ ：传统统计学习中的正则化强度；λ 越大，模型越简单。

C：C = 1 / λ，C 越小，正则化越强。

交叉验证：

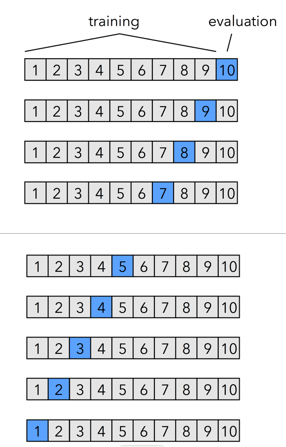
交叉验证通过反复划分数据集，使“训练-验证”过程多次执行并聚合结果，从而同时满足模型选择与性能估计两大需求。

将数据集分成十份：每次取一份，直至10分都被取进行训练测试，聚合结果，使所有数据都能被训练。

 代码示例：

from sklearn.model_selection import cross_val_score
score = cross_val_score(lr,os_x_train,os_y_train,cv=8,scoring='recall')

第一行：导入可实现交叉验证的库

第二行：cv = 8：表示分为八份

scoring='recall' 以召回率（TP/(TP+FN)）作为评价指标，契合信用卡欺诈检测场景对漏报成本的极端敏感性。

 二、模型优化

1.解决样本数据的不平衡

1.1 下采样 

 思想：把多数类（正常交易）随机砍掉一部分，让 0 和 1 的数量一样多。

 优点：简单、快速、不增加数据量。
缺点：白白扔掉大量正常交易的信息，可能损失精度

 示例代码：

positive = data[data['Class']==0] #正常
negetive = data[data['Class']==1] #老赖
positive = positive.sample(len(negetive)) #使多数类折掉一部分和少数类一样多
data=pd.concat([positive,negetive]) #将两个数据结合
x_1 = data.drop("Class",axis=1) #去除最后一列剩下的作为x
y_1 = data.Class #最后一列作为y

注：采用下采样时，如果数据较少，cv值取小一些，效果会更好。 

1.2 上采样

思想：给少数类造新样本，而不是删除多数类。
最常用的算法是 SMOTE：在少数类样本之间插值

 示例代码：

from imblearn.over_sampling import SMOTE #导入库
oversample = SMOTE(random_state=0)  
os_x_train,os_y_train = oversample.fit_resample(x_train,y_train) #在少数类样本之间做插值，合成新的少数类样本，使两类样本达到平衡

 总代码：

下采样

import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegressiondata = pd.read_csv("creditcard.csv")
from sklearn.preprocessing import StandardScaler #z标准化
scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])
data = data.drop(['Time'],axis=1)
x = data.drop("Class",axis=1)
y = data.Class
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3,random_state=1000)
positive = data[data['Class']==0]
negetive = data[data['Class']==1]
positive = positive.sample(len(negetive))
data=pd.concat([positive,negetive])
x_1 = data.drop("Class",axis=1)
y_1 = data.Class# lr.fit(x_train,y_train)
# y_predict=lr.predict(x_test)
# score = lr.score(x_test,y_test)
#from sklearn.model_selection import cross_val_score
scores = []
d = [0.01,0.1,1,10,100]
for i in d:lr = LogisticRegression(C=i,max_iter=1000)score = cross_val_score(lr,x_1,y_1,cv=5,scoring='recall')scores_mean = sum(score)/len(score)scores.append(scores_mean)
best = d[np.argmax(scores)]
print("最优惩罚因子为{}".format(best))
lr = LogisticRegression(C=best,max_iter=1000)
lr.fit(x_1,y_1)
y_predict = lr.predict(x_test)
score = lr.score(x_test,y_test)from sklearn import metrics
print(metrics.classification_report(y_test,y_predict))

 上采样：

import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegressiondata = pd.read_csv("creditcard.csv")
from sklearn.preprocessing import StandardScaler #z标准化
scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])
data = data.drop(['Time'],axis=1)
x = data.drop("Class",axis=1)
y = data.Class
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3,random_state=1000)
from imblearn.over_sampling import SMOTE
oversample = SMOTE(random_state=0)
os_x_train,os_y_train = oversample.fit_resample(x_train,y_train)
# lr.fit(x_train,y_train)
# y_predict=lr.predict(x_test)
# score = lr.score(x_test,y_test)
#from sklearn.model_selection import cross_val_score
scores = []
c_choose = [0.01,0.1,1,10,100]  #赋予C不同的值
for i in c_choose:lr = LogisticRegression(C=i,max_iter=1000)score = cross_val_score(lr,os_x_train,os_y_train,cv=8,scoring='recall')scores_mean = sum(score)/len(score)scores.append(scores_mean)
best = d[np.argmax(scores)]
print("最优惩罚因子为{}".format(best))
lr = LogisticRegression(C=best,max_iter=1000)
lr.fit(os_x_train,os_y_train)
y_predict = lr.predict(x_test)
score = lr.score(x_test,y_test)from sklearn import metrics
print(metrics.classification_report(y_test