【AI论文】MUR：面向大型语言模型的动量不确定性引导推理

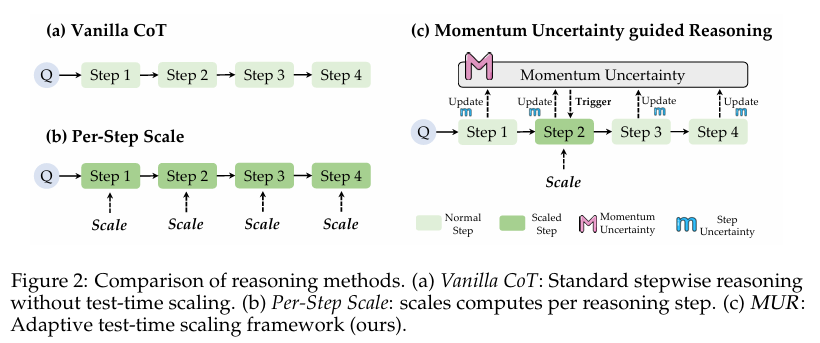
摘要：大型语言模型（LLMs）在推理密集型任务上展现出了卓越的性能，然而，优化其推理效率仍是一个亟待解决的挑战。虽然测试时扩展（Test-Time Scaling，TTS）能够提升推理质量，但往往会导致过度思考，在冗余计算上浪费算力资源。本研究旨在探讨如何在无需额外训练的情况下，高效且自适应地指导大型语言模型在测试时进行扩展。受物理学中动量概念的启发，我们提出了动量不确定性引导推理（Momentum Uncertainty-guided Reasoning，MUR）方法，该方法通过追踪并累积随时间变化的阶段性不确定性，动态地为关键推理步骤分配思考资源。为了支持推理时的灵活控制，我们引入了伽马控制（gamma-control）这一简单机制，通过单一超参数即可调整推理资源分配。我们提供了深入的理论证明，以支持MUR在稳定性和偏差方面的优越性。我们在四个具有挑战性的基准测试集（MATH-500、AIME24、AIME25和GPQA-diamond）上，使用不同规模的最新Qwen3模型（17亿、40亿和80亿参数）对MUR与各种TTS方法进行了全面评估。结果显示，MUR在平均减少超过50%计算量的同时，将准确率提升了0.62%至3.37%。Huggingface链接：Paper page，论文链接：2507.14958

研究背景和目的

研究背景：

随着大型语言模型（LLMs）在自然语言处理领域的广泛应用，其在推理密集型任务（如逻辑推理、数学问题和游戏策略）中展现出了令人瞩目的性能。然而，尽管这些模型在推理质量上有所提升，但其推理效率仍然是一个亟待解决的问题。传统的测试时扩展（Test-Time Scaling, TTS）方法，如通过强化学习或并行采样来增加计算量，虽然能够提高推理质量，但往往导致“过度思考”（overthinking），即在简单步骤上浪费大量算力资源进行冗余计算，而复杂步骤却可能得不到足够的计算资源。

具体而言，现有TTS方法存在两大问题：一是它们通常均匀地分配计算资源，没有区分关键步骤和非关键步骤，导致计算效率低下；二是这些方法往往需要额外的训练过程，增加了模型的复杂性和部署成本。因此，如何在不增加额外训练的情况下，高效且自适应地指导LLMs在测试时进行扩展，成为了一个重要的研究方向。

研究目的：

本研究旨在提出一种新的方法，即动量不确定性引导推理（Momentum Uncertainty-guided Reasoning, MUR），以解决上述问题。MUR方法受物理学中动量概念的启发，通过追踪并累积随时间变化的阶段性不确定性，动态地为关键推理步骤分配计算资源。具体而言，本研究的目标包括：

1. 提高推理效率：通过动态分配计算资源，减少在简单步骤上的冗余计算，从而降低整体计算成本。
2. 保持或提升推理质量：确保关键步骤得到足够的计算资源，从而维持或提高推理的准确性。
3. 无需额外训练：提出一种无需额外训练的推理时控制方法，降低模型的复杂性和部署成本。

研究方法

1. 动量不确定性建模：

MUR方法的核心在于动量不确定性的建模。该方法通过递归地计算历史步骤的不确定性，得到当前步骤的动量不确定性。具体而言，设第t步的不确定性为m_t，动量不确定性M_t定义为：

\[ M_t = \alpha M_{t-1} + (1 - \alpha) m_t \]

其中，α是一个超参数，控制历史不确定性的衰减速度。通过这种方式，M_t能够反映当前推理路径的整体不确定性，同时强调近期步骤的不确定性。

2. γ控制机制：

为了支持推理时的灵活控制，MUR引入了γ控制机制。该机制通过一个简单的超参数γ来调整推理预算。具体而言，当且仅当满足以下条件时，对当前步骤进行扩展计算：

\[ \exp(m_t) > \frac{\exp(M_{t-1})}{\gamma} \]

这一条件意味着，只有当当前步骤的不确定性显著高于历史平均不确定性时，才会触发扩展计算。通过调整γ的值，可以灵活控制推理预算和性能之间的平衡。

3. 实验设置：

为了验证MUR方法的有效性，本研究在四个具有挑战性的基准测试集（MATH-500、AIME24、AIME25和GPQA-diamond）上进行了全面评估。实验使用了不同规模的最新Qwen3模型（17亿、40亿和80亿参数）。为了公平比较，实验还实现了多种TTS方法作为基线，包括Guided Search、LLM As a Critic和ϕ-Decoding等。

研究结果

1. 计算成本显著降低：

实验结果表明，MUR方法在不降低推理准确性的前提下，显著降低了计算成本。具体而言，在四个基准测试集上，MUR平均减少了超过50%的计算量。例如，在MATH-500测试集上，使用Qwen3-8B模型时，MUR方法将计算量从Per-Step Scale方法的27,672个token减少到了7,930个token，同时准确率还有所提升。

2. 推理准确性提升：

除了降低计算成本外，MUR方法还在多个基准测试集上提升了推理准确性。具体而言，MUR方法在MATH-500、AIME24、AIME25和GPQA-diamond测试集上的准确率分别提升了0.62%、3.37%、1.47%和2.00%。这些提升表明，MUR方法能够有效地识别关键步骤，并为其分配足够的计算资源。

3. 灵活控制推理预算：

通过调整γ的值，MUR方法能够灵活地控制推理预算和性能之间的平衡。实验结果表明，随着γ值的增加，推理准确性和计算量均有所增加。这一特性使得MUR方法能够适应不同场景下的需求，无论是追求高效率还是高准确性。

研究局限

尽管MUR方法在降低计算成本和提高推理准确性方面展现出了显著优势，但本研究仍存在一些局限性。

1. 超参数选择：

MUR方法的有效性在一定程度上依赖于超参数α和γ的选择。尽管实验结果表明，MUR方法在多个基准测试集上对这两个超参数的选择具有一定的鲁棒性，但不同的任务和数据集可能仍需要针对性的调优。未来研究可以探索更自适应的超参数调整方法。

2. 复杂推理任务：

尽管MUR方法在当前的基准测试集上展现出了良好的性能，但对于更加复杂的推理任务（如涉及多步推理和跨领域知识的任务），其有效性仍有待验证。未来研究可以进一步拓展MUR方法的应用场景，并探索其在更复杂任务中的表现。

3. 理论分析的局限性：

尽管本研究提供了深入的理论分析来支持MUR方法的优越性，但这些分析仍基于一定的假设和简化。未来研究可以进一步完善理论分析框架，以更全面地解释MUR方法在不同场景下的工作原理和性能表现。

未来研究方向

针对上述研究局限，未来研究可以从以下几个方面展开：

1. 自适应超参数调整：

探索更自适应的超参数调整方法，以减少对人工调优的依赖。例如，可以引入强化学习或元学习的方法来自动调整α和γ的值，以适应不同的任务和数据集。

2. 拓展应用场景：

将MUR方法应用于更复杂的推理任务中，如涉及多步推理、跨领域知识和外部知识库的任务。通过拓展应用场景，可以进一步验证MUR方法的有效性和鲁棒性。

3. 完善理论分析：

进一步完善理论分析框架，以更全面地解释MUR方法在不同场景下的工作原理和性能表现。例如，可以探索MUR方法在不同类型不确定性下的表现，以及其与现有TTS方法的关系和差异。

4. 结合其他优化技术：

探索将MUR方法与其他优化技术（如模型剪枝、量化等）相结合的可能性，以进一步提升大型语言模型的推理效率和性能。

5. 实时推理优化：

研究如何在实时推理场景下应用MUR方法，以满足低延迟和高准确性的双重需求。这可能需要进一步优化MUR方法的计算复杂度和资源消耗。

总之，本研究提出的MUR方法为大型语言模型的推理效率优化提供了一种新的思路和方法。未来研究可以围绕上述方向展开，以进一步推动大型语言模型在推理任务中的应用和发展。