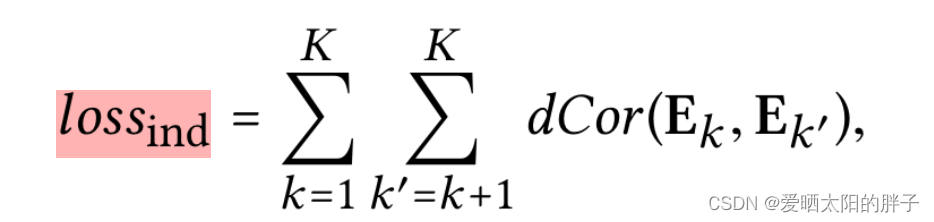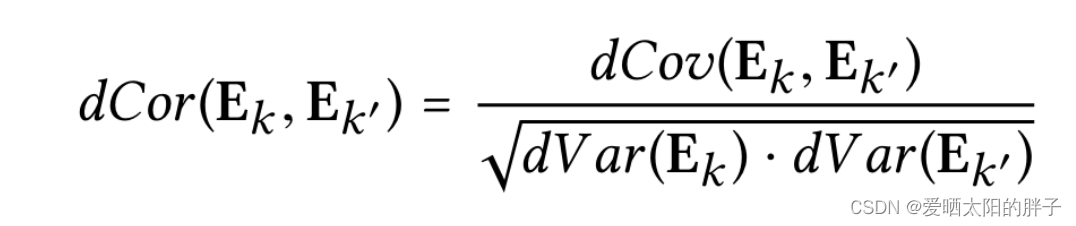Disentangled Graph Collaborative Filtering
代码地址:https://github.com/ xiangwang1223/disentangled_graph_collaborative_filtering
Background:
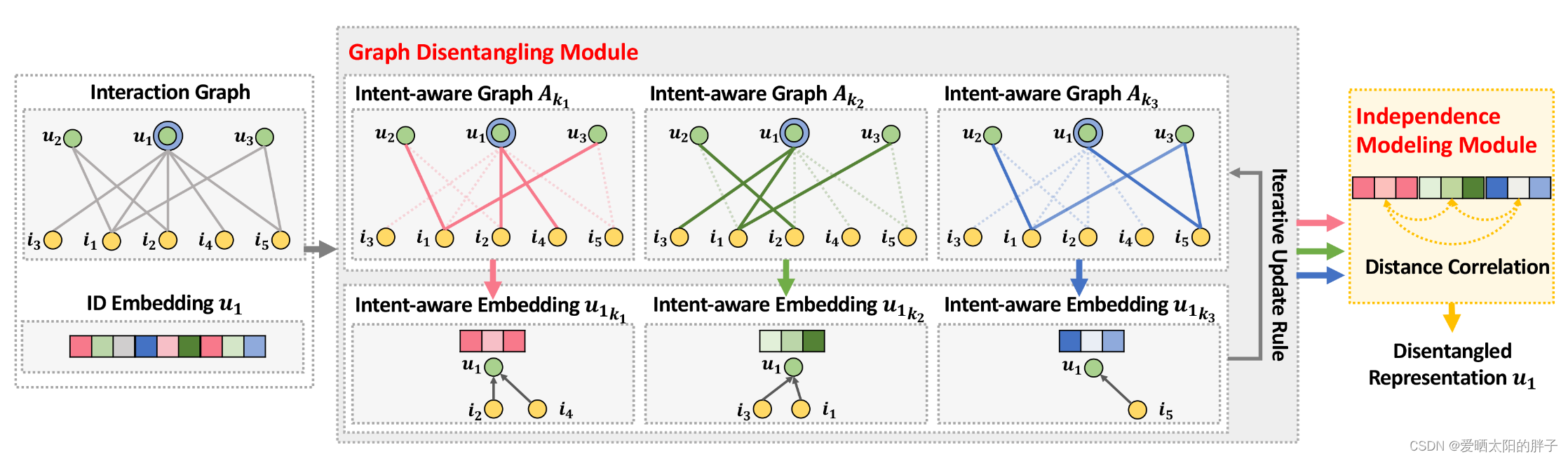
现有模型在很大程度上以统一的方式对用户-物品关系进行建模(将模型看做黑盒,历史交互作为输入,Embedding作为输出。),这会忽略用户意图的多样性(用户看一个视频可能是因为消磨时间、喜欢里面的演员等多种意图)导致representation次优。本文提出,将embedding划分成多个部分,每一部分单独表示一种意图,各部分之间相互独立,实现意图的解耦。
例:假设Embedding长度为N,意图数量为K,划分后每一部分长度为,即
u = (,
,……,
),
=
。物品i的也进行同样的划分:
i = (
PRELIMINARY
1、本文构建了多个意图感知图,, 其中
=
, u,i
表示u-i之间产生过交互, 表示用户u和物品i发生交互是因为意图k的分数,不难看出意图感知图是一个带权图
2、itent-aware图不是用户-物品交互二部图的子图,二者图形结构是一样的,但用户的表示是,物品的表示为
3、用户和物品的交互存在多个意图, 构成意图分布: ,
表示用户u和物品i发生交互是因为意图k的自信强度,整体表示用户u和物品i发生交互因为各意图的自信度大小。
4、本文用邻接矩阵存储和表示意图感知图(带权图)
。元素
,表示用户u因为意图k和物品i发生交互的自信程度为x。
METHODOLOGY(本文重点是两个迭代更新方法)
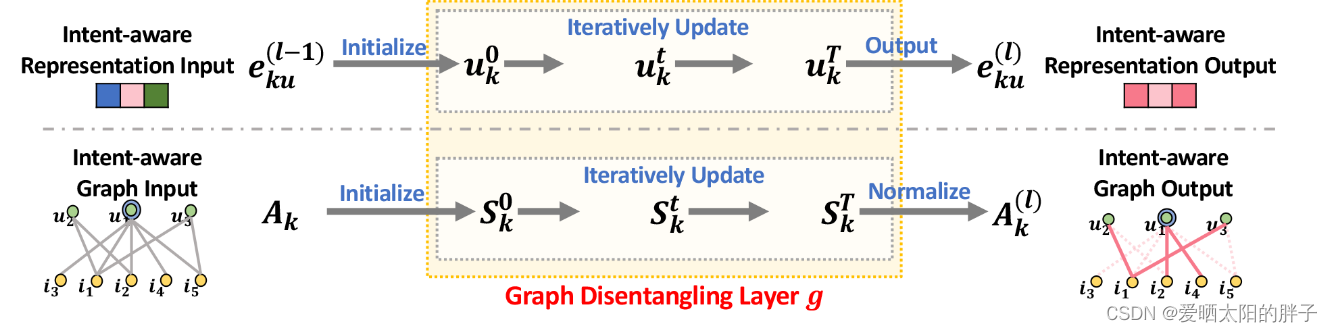
初始化:
将用户u和 i 的embedding向量初始化为随机数。中u-i发生过交互的位置初始化为1(开始时假定用户意图分布相同),并将初始化后的矩阵记为
,如上图下部分所示。
更新机制:
本文采用迭代更新机制,不管是特征更新还是意图感知图的更新,都重复T次,目的是使结果更贴近实际。下文中 ,意图感知图和意图感知表示,交替更新T次(虽然二者都进行了迭代更新,但主要目的还是为了得到更好的意图感知表示,或者可以说意图感知图的更新目的是为了得到更真实的用户意图自信程度,在消息传递时传递更有效的信息。)。
意图感知特征更新
执行T次GNN,首先进行一阶邻居消息聚合,迭代T次得到,再对2……L跳邻居进行消息聚合,方法不变,得到
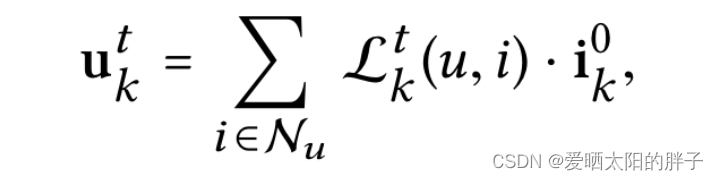
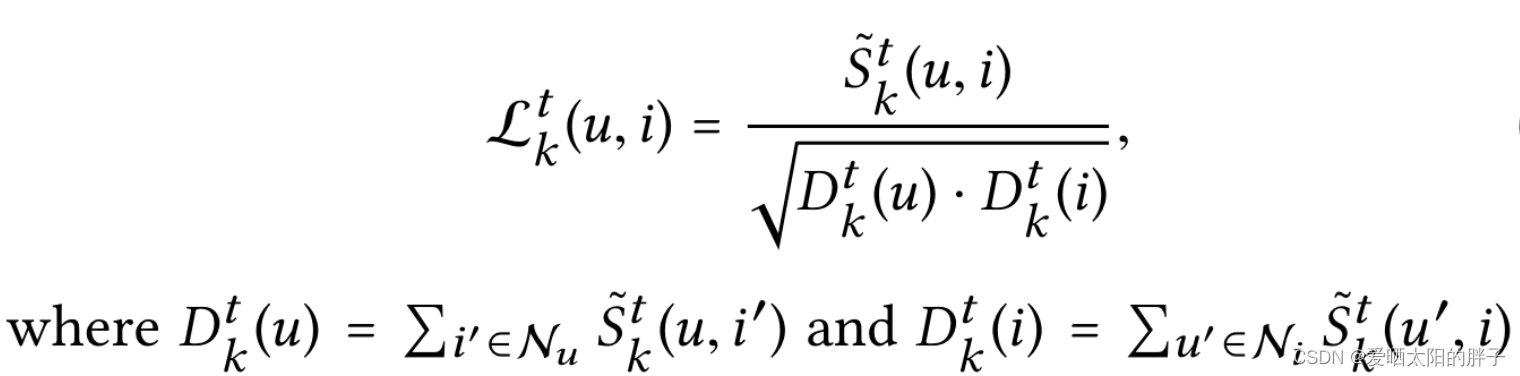
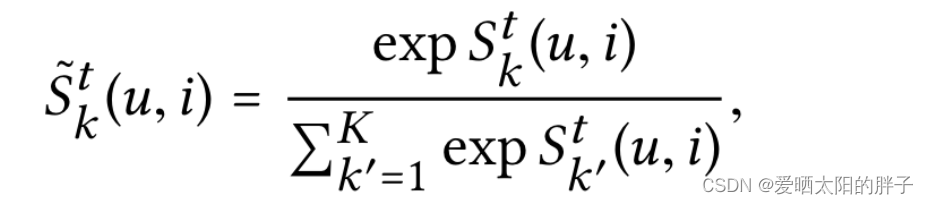
:可理解为注意力,u和i发生交互是因为意图k的自信度越大,则从物品在k上的特征提取的越多。
:前文说过,用户和物品交互可能因为多个意图,用户与物品交互的意图分布为:
,这里对各意图做normalization。
意图感知图更新
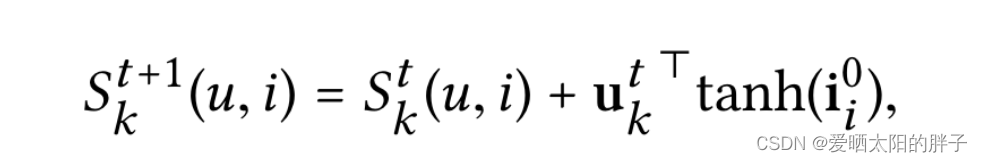
用意图感知特征去更新意图感知图。
层聚合
将得到的0……L层消息聚合后的特征表示做SUM作为用户最终的特征表示。
独立性建模
本文将用户特征表示,划分成多个意图,各意图之间独立,实现意图的解纠缠。为了使各意图互相独立,本文引入距离相关性损失: