论文阅读|CVPR 2025|Mamba进一步研究|GroupMamba

论文地址：pdf
代码地址：code

---

1.研究背景与动机

• 现有模型局限：基于 SSM 的视觉模型（如 Mamba、VMamba）在处理视觉任务时存在两大挑战：一是大模型训练不稳定（参数增多时性能下降）；二是计算效率低（通道数增加会导致参数和计算成本激增），难以平衡性能与效率。

• 核心目标：设计参数高效、训练稳定的 SSM 模型，通过改进结构增强跨通道交互和空间依赖建模，在图像分类、检测、分割等任务中实现更优性能。

---

2. 核心方法

2.1 预备知识:mamba-ssm

状态空间模型:经典的状态空间模型（SSMs）表示一个连续系统，它将输入序列$x(t)\in {\mathbb{R}}^L$映射到 latent 空间表示$h(t)\in {\mathbb{R}}^N$，然后基于该表示预测输出序列$y(t)\in {\mathbb{R}}^L$。从数学上讲，SSM可描述为：
$$\begin{array}{c}{h}^{\prime }(t)=Ah(t)+Bx(t),y(t)=Ch(t)\end{array}$$
其中$A\in {\mathbb{R}}^{N\times N}$、$B\in {\mathbb{R}}^{N\times 1}$和$C\in {\mathbb{R}}^{1\times N}$是可学习参数。

离散化:为了使连续状态空间模型（SSMs）适用于深度学习框架，实现离散化操作至关重要。通过引入时间尺度参数$\Delta \in \mathbb{R}$并采用广泛使用的零阶保持（ZOH）作为离散化规则，可以推导出A和B的离散化版本（分别表示为$\overline{A}$和$\overline{B}$），据此，式1可重写为离散形式：
$$\begin{array}{c}\begin{array}{rl}h(t)& =\overline{A}h(t-1)+\overline{B}x(t),y(t)=Ch(t),\\ \text{where }\overline{A}& =e^{\Delta A},\overline{B}=(\Delta A{)}^{-1}\left(e^{\Delta A}-I\right)\Delta B\approx \Delta B\end{array}\end{array}$$
离散化的详细推导可见这篇文章
其中$I$表示单位矩阵。

2.2 整体架构

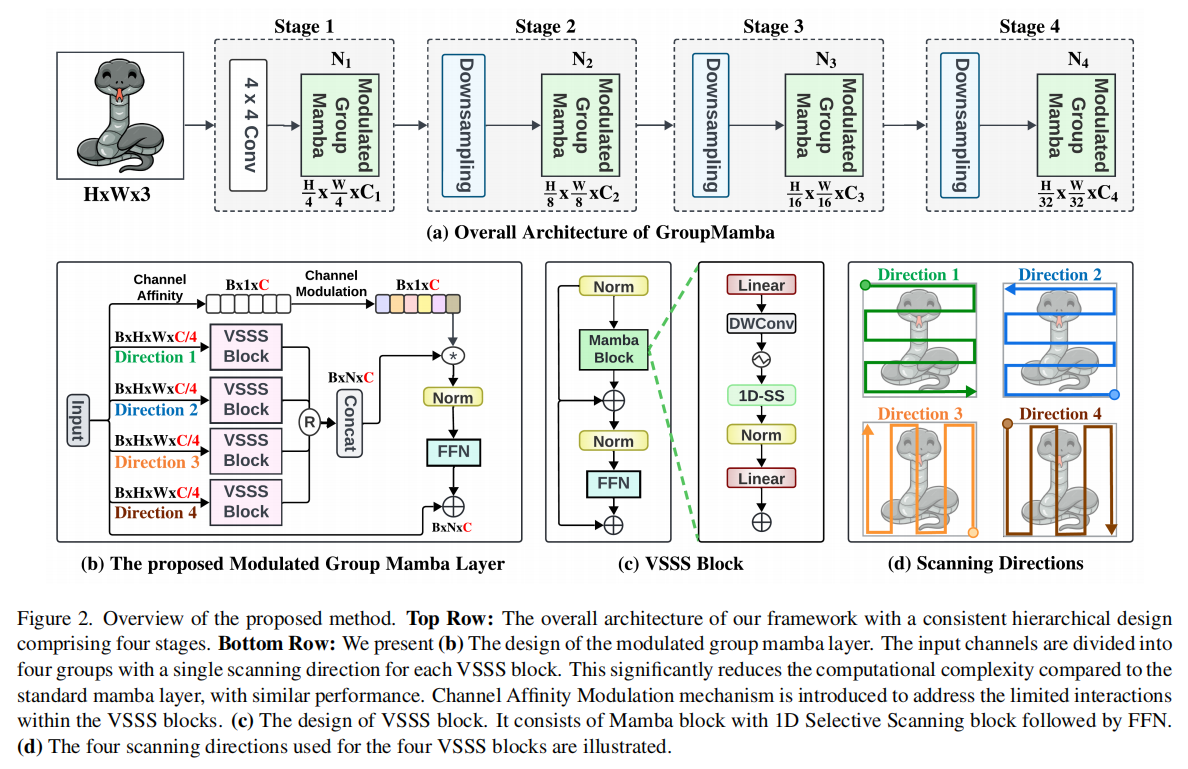
如图2（a）所示，模型采用分层架构，类似于Swin-Transformer，包含四个阶段，可高效处理不同分辨率的图像。假设输入图像为$I\in {\mathbb{R}}^{H_0\times W_0\times 3}$，我们首先应用补丁嵌入层将图像分割为4×4的非重叠补丁（实质还是一个特征，只是包含了4×4的非重叠补丁的信息），并将每个补丁嵌入到$C$维特征向量中。补丁嵌入层通过两个3×3卷积实现，步长为2。这在第一阶段产生大小为$H_1\times W_1\times C$的特征图，其中$H_1=H_0/4$，$W_1=W_0/4$。这些特征图通过$N_1$个提出的调制组Mamba块（详见3.3节）处理。在后续每个阶段中，下采样层合并2×2区域的补丁，随后是$N_2,N_3,N_4$个调制组Mamba层块。因此，第二、三、四阶段的特征大小分别为$H_2\times W_2\times 2C$、$H_3\times W_3\times 4C$和$H_4\times W_4\times 8C$，其中$H_{i+1}=H_i/2$，$W_{i+1}=W_i/2$。

2.3 调制组Mamba层

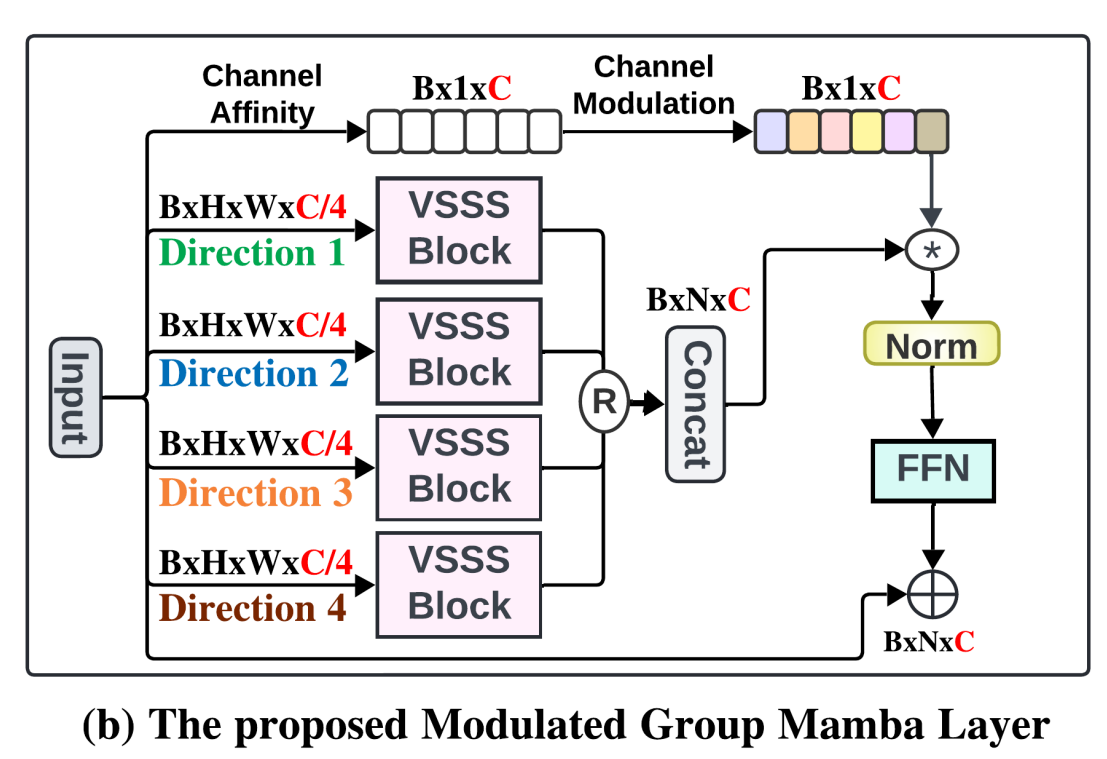
在式3中给出了所提出的调制组Mamba层（图2（b））对输入序列$X_{in}\in {\mathbb{R}}^{B\times H\times W\times C}$的整体操作，其中$B$是批大小，$C$是输入通道数，$H/W$是特征图的高度和宽度。
$$\begin{array}{c}\begin{array}{rl}{X}_{GM}& =\text{GroupedMamba}\left(X_{in},\Theta \right)\\ X_{CAM}& =\text{CAM}\left(X_{GM},\text{Affinity}\left(X_{in}\right)\right)\\ X_{out}& =X_{in}+\text{FFN}\left(\text{LN}\left(X_{CAM}\right)\right)\end{array}\end{array}$$

其中，$X_{GM}$是式6的输出，$X_{CAM}$是式9的输出，LN是层归一化操作，FFN是式5描述的前馈网络，$X_{out}$是调制组Mamba块的最终输出。各个操作（即分组Mamba算子、分组Mamba算子中使用的VSSS块和CAM算子）分别在2.3.1节、2.3.2节和2.3.3节中介绍。

2.3.1 视觉单选择性扫描（VSSS）块

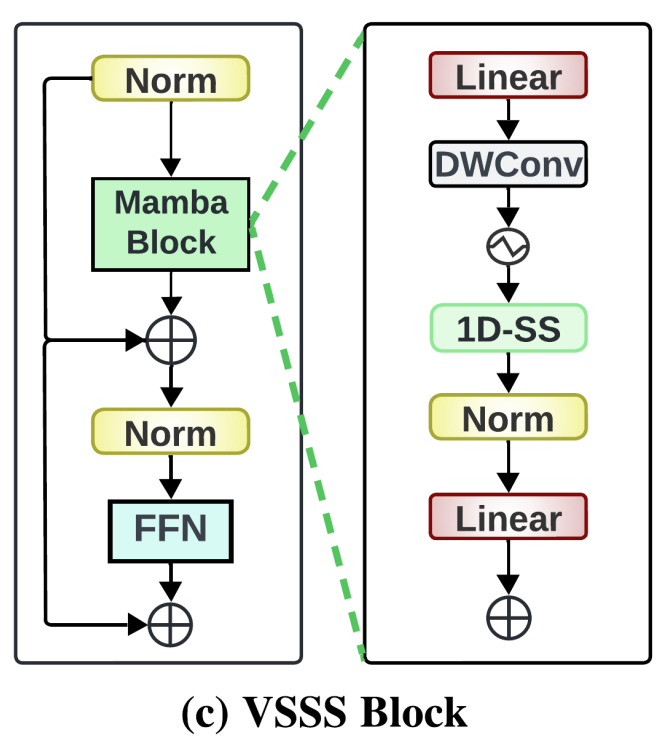
VSSS块（图2（c））是基于Mamba算子的令牌和通道混合器，由一个Mamba块和一个前馈网络组成，每个网络前都有一个层归一化。从数学上讲，对于输入令牌序列$Z_{in}$，VSSS块执行式4中描述的操作：
$$\begin{array}{c}\begin{array}{rl}& Z_{out}^{\prime }=Z_{in}+\text{Mamba}\left(\text{LN}\left(Z_{in}\right)\right)\\ & Z_{out}=Z_{out}^{\prime }+\text{FFN}\left(\text{LN}\left(Z_{out}^{\prime }\right)\right)\end{array}\end{array}$$

其中，$Z_{out}$是输出序列，Mamba是式2中描述的离散化Mamba SSM算子。
$$\begin{array}{c}\text{FFN}\left(\text{LN}\left(Z_{out}^{\prime }\right)\right)=\text{GELU}\left(\text{LN}\left(Z_{out}^{\prime }\right)W_1+b_1\right)W_2+b_2\end{array}$$

其中，GELU是激活函数，$W_1,W_2$和$b_1,b_2$是线性投影的权重和偏置。

2.3.2 分组Mamba算子

鉴于Mamba在输入序列通道数较多时计算效率较低，我们受分组卷积启发，提出了一种分组变体算子。分组Mamba操作是2.3.1节中介绍的VSSS块的变体，其中输入通道被分为多个组，VSSS算子分别应用于每个组。具体来说，我们将输入通道分为4组，每组大小为$C/4$，每个组应用一个独立的VSSS块。因此，所提出的分组Mamba算子通过将通道分成更小的组来提高模型效率。为了更好地建模输入中的空间依赖，四个组中的每个组都沿四个空间方向之一扫描（图2（d）所示的左右、右左、上下、下上）。

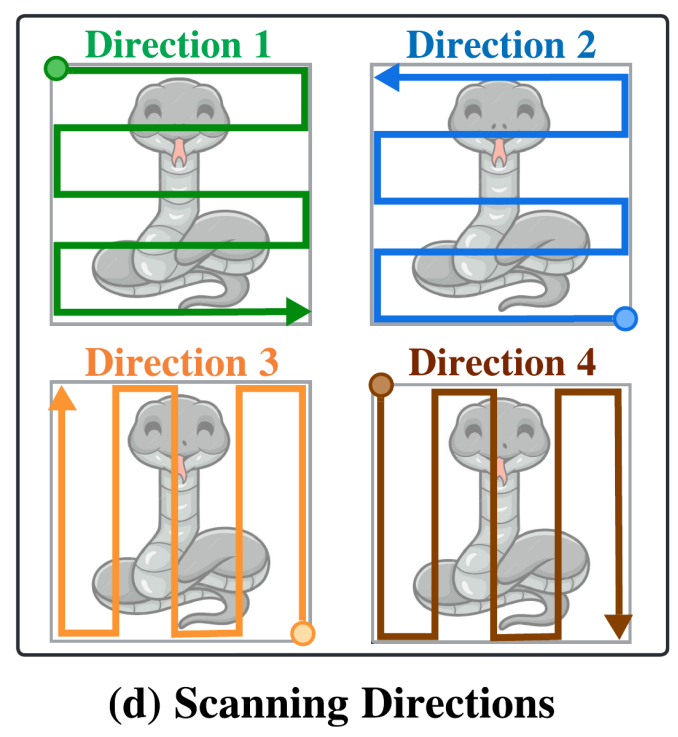
设$G=4$为表示四个扫描方向（左右、右左、上下、下上）的组数。我们从输入序列$X_{in}$中形成四个序列，即$X_{LR}$、$X_{RL}$、$X_{TB}$和$X_{BT}$，每个序列的形状为$(B,H,W,C/4)$，分别对应上述四个方向。然后将它们展平为单个令牌序列，形状为$(B,N,C/4)$，其中$N=W\times H$是序列中的令牌数。四个组中每个组的参数可分别由${\Theta }_{LR}$、${\Theta }_{RL}$、${\Theta }_{TB}$和${\Theta }_{BT}$指定，分别代表每个VSSS块的参数。

基于上述定义，分组Mamba算子的整体关系如式6所示：
$$\begin{array}{c}\begin{array}{rl}{X}_{GM}& =\text{GroupedMamba}\left(X_{in},\Theta \right)=\text{Concat}(\\ & \text{VSSS}\left(X_{LR},{\Theta }_{LR}\right),\text{VSSS}\left(X_{RL},{\Theta }_{RL}\right),\\ & \text{VSSS}\left(X_{TB},{\Theta }_{TB}\right),\text{VSSS}\left(X_{BT},{\Theta }_{BT}\right))\end{array}\end{array}$$

其中：

• $X_{LR}$、$X_{RL}$、$X_{TB}$和$X_{BT}$表示沿相应方向扫描的输入张量。
• ${\Theta }_{LR}$、${\Theta }_{RL}$、${\Theta }_{TB}$和${\Theta }_{BT}$表示每个方向的VSSS块参数。
• 每个Mamba算子的输出被重新整形为$(B,H,W,C/4)$，并拼接回形状为$(B,H,W,C)$的令牌序列$X_{GM}$。

2.3.3 通道亲和调制（CAM）

就其本身而言，分组Mamba算子可能存在一个缺点，即跨通道的信息交换有限，因为组中的每个算子仅对$C/4$个通道进行操作。为促进跨通道的信息交换，我们提出了通道亲和调制算子，该算子重新校准通道方向的特征响应，以增强网络的表示能力。在该块中，我们首先对输入进行平均池化以计算通道统计量，如式7所示：
$$\begin{array}{c}\text{ChannelStat}\left(X_{in}\right)=\text{AvgPool}\left(X_{in}\right)\end{array}$$
其中，$X_{in}$是输入张量，$AvgPool$表示全局平均池化操作。接下来是如式8所示的亲和计算操作：
$$\begin{array}{c}\text{Affinity}\left(X_{in}\right)=\sigma \left(W_2\delta \left(W_1\text{ChannelStat}\left(X_{in}\right)\right)\right)\end{array}$$

其中，$\delta$和$\sigma$表示非线性函数，$W_1$和$W_2$是可学习权重。$\sigma$的作用是为每个通道分配一个重要性权重以计算亲和度。亲和度计算的结果用于重新校准分组Mamba算子的输出，如式9所示：
$$\begin{array}{c}{X}_{CAM}=\text{CAM}\left(X_{GM},\text{Affinity}\left(X_{in}\right)\right)=X_{GM}\cdot \text{Affinity}\left(X_{in}\right)\end{array}$$

其中，$X_{CAM}$是重新校准的输出，$X_{GM}$是式6中四个VSSS组的拼接输出，$X_{in}$是输入张量，$\text{Affinity}(X_{in})$是从式8中的通道亲和计算操作获得的通道方向注意力分数。

虽然CAM模块采用的平均池化和亲和过程类似于挤压-激励（SE）块，但它引入了一种独特的机制，专门为多组变换中的跨通道注意力量身定制。具体而言，CAM允许组间信息交换，以克服“分组Mamba算子”固有的限制（即仅允许组内交互）。相比之下，SE块通常专注于重新校准单个特征组，尚未在基于Mamba的架构中进行研究。

2.4 蒸馏损失函数

因为Mamba在扩展到大型模型时训练不稳定。为缓解这一问题，我们建议在标准交叉熵目标之外利用蒸馏目标。知识蒸馏包括训练学生模型从教师模型的行为中学习，方法是最小化分类损失和蒸馏损失的组合。蒸馏损失通过教师模型和学生模型的logits之间的交叉熵目标计算。给定学生模型的$logits(Z_s)$、教师模型（在我们的案例中为RegNetY-16G）的$logits(Z_t)$、真实标签$y$ 以及 教师的硬决策$y_t={\text{argmax}}_c{Z}_t(c)$，联合损失函数如式10所示：
$$\begin{array}{c}{\mathcal{L}}_{\text{total }}=\alpha {\mathcal{L}}_{\text{CE}}\left(Z_s,y\right)+(1-\alpha ){\mathcal{L}}_{\text{CE}}\left(Z_s,y_t\right)\end{array}$$

其中，${\mathcal{L}}_{\text{CE}}$是交叉熵损失，$\alpha$是权重参数。我们在补充材料中证明，引入蒸馏损失可增强训练稳定性，为更大的模型变体带来持续的性能提升。

---

3. 实验结果

3.1 图像分类任务

3.2 目标检测任务

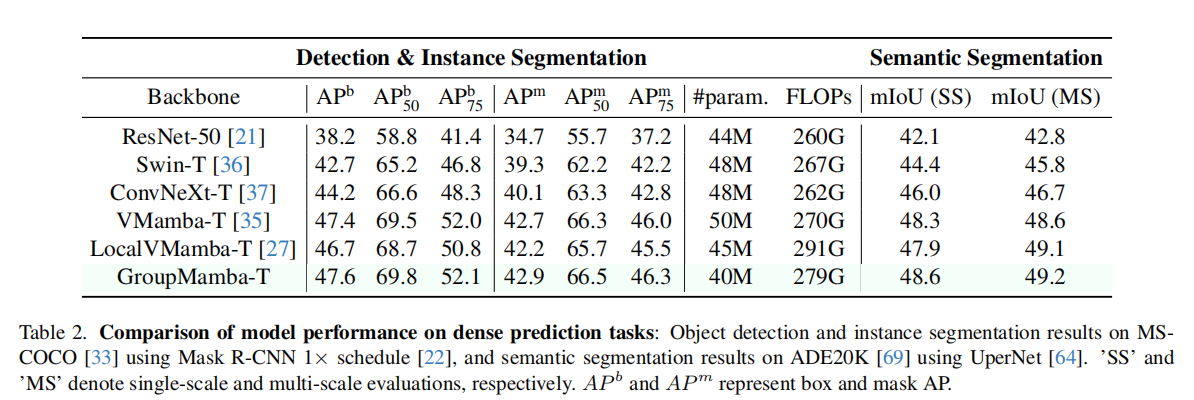
3.3 语义分割任务

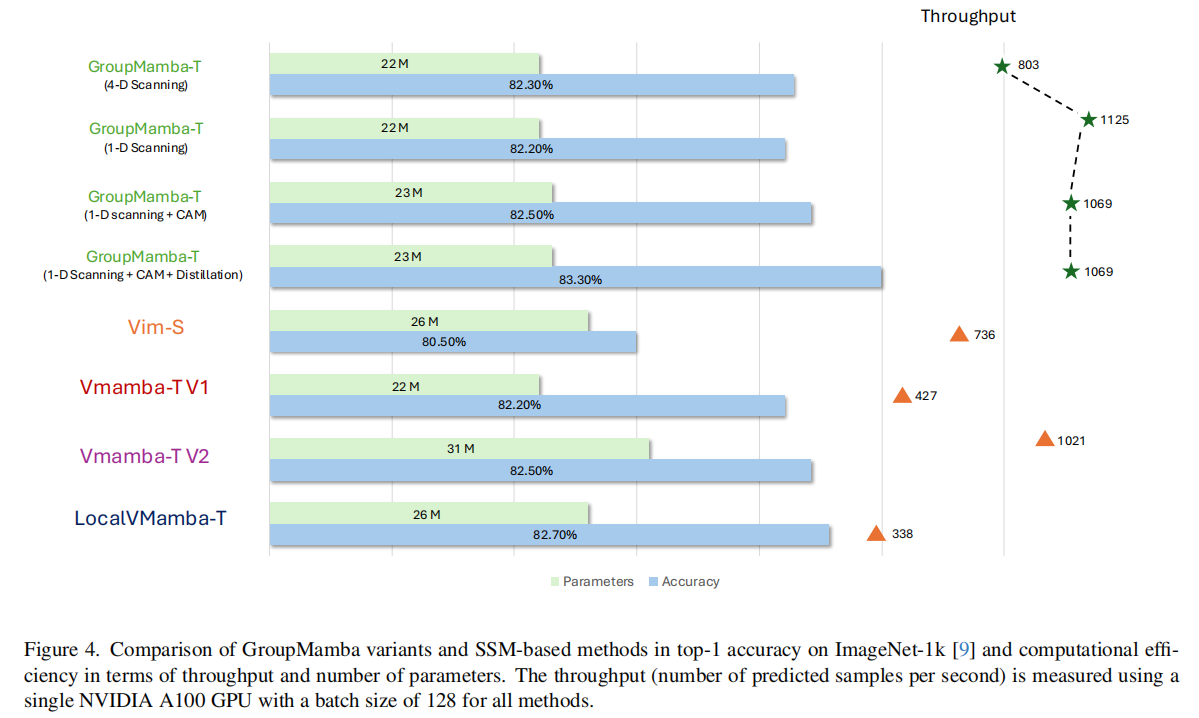
3.4 消融实验

---

4.局限性与结论

4.1 局限性

• 任务覆盖范围有限：研究主要集中在图像分类、目标检测、实例分割和语义分割任务，尚未在视频识别、时间序列数据等更广泛的视觉或序列任务中验证模型的泛化能力
• 大模型稳定性验证不足：尽管引入蒸馏损失缓解了训练不稳定性，但针对更大参数规模模型（如超大规模 GroupMamba）的稳定性和性能表现仍需进一步探索

4.2 结论

核心贡献有效性：提出的调制组 Mamba 层通过分组扫描和多方向空间建模，在降低计算成本的同时增强了特征表达能力；通道亲和调制（CAM）算子有效解决了分组操作导致的跨通道交互不足问题；蒸馏损失函数显著提升了大模型训练的稳定性

• 性能优势：GroupMamba 系列模型在多个视觉任务中表现优异，例如 tiny 变体（23M 参数）在 ImageNet-1K 上实现 83.3% 的 Top-1 准确率，参数效率比同类 Mamba 模型高 26%；base 变体（57M 参数）准确率达 84.5%，参数比 VMamba-B 少 36%
• 效率与性能平衡：GroupMamba 在保持状态空间模型（SSMs）线性复杂度优势的同时，实现了参数效率与任务性能的更优权衡，为高效视觉骨干网络设计提供了新方案
• 未来方向：计划将模型扩展到视频识别、时间序列等任务，进一步验证调制组 Mamba 层的泛化能力和局限性

---