Python数组仿射变换
文章目录
- 仿射变换
- 坐标变换的逻辑
- scipy实现
仿射变换
前面提到的平移、旋转以及缩放,都可以通过一个变换矩阵来实现,以二维空间中的变换矩阵为例,记点的坐标向量为 ( x , y , 1 ) (x,y,1) (x,y,1),则平移矩阵可表示为
[ 1 0 T x 0 1 T y 0 0 1 ] \begin{bmatrix} 1&0&T_x\\0&1&T_y\\0&0&1 \end{bmatrix} 100010TxTy1
旋转矩阵可表示为
[ cos θ sin θ − sin θ cos θ ] \begin{bmatrix} \cos\theta&\sin\theta\\-\sin\theta&\cos\theta \end{bmatrix} [cosθ−sinθsinθcosθ]
在scipy.ndimage中,提供了专门的仿射变换函数affine_transform,用于坐标的仿射变换。
坐标变换的逻辑
假设现在有一个矩阵
[ a b c d ] \begin{bmatrix}a&b\\c&d\end{bmatrix} [acbd]
则 a , b , c , d a,b,c,d a,b,c,d的坐标为 ( 0 , 0 ) , ( 1 , 0 ) , ( 0 , 1 ) , ( 1 , 1 ) (0,0),(1,0),(0,1),(1,1) (0,0),(1,0),(0,1),(1,1),那么假设现在给出一个变换矩阵
M = [ 1 1 1 1 ] M=\begin{bmatrix}1&1\\1&1\end{bmatrix} M=[1111]
则坐标 ( 0 , 1 ) (0,1) (0,1)变为
[ 0 1 ] [ 1 1 1 1 ] = [ 1 1 ] \begin{bmatrix}0&1\end{bmatrix}\begin{bmatrix}1&1\\1&1\end{bmatrix}=\begin{bmatrix}1&1\end{bmatrix} [01][1111]=[11]
从而 ( 1 , 1 ) (1,1) (1,1)处的值变为 c c c。另一方面 ( 1 , 0 ) (1,0) (1,0)坐标也变为 ( 1 , 1 ) (1,1) (1,1),所以 ( 1 , 1 ) (1,1) (1,1)处也可能为 b b b。
scipy实现
仿射变换函数支持output, order, mode, cval以及prefilter这5个参数,此外,二者均支持output_shape参数,用于调整输出的数组维度。除了这些参数之外,仿射变换的定义式为affine_transform(input, matrix, offset=0.0, ),其中matrix为变换矩阵,当输入不同维度的矩阵时,含义不同,设 n n n为输入数组的维度,则matrix的矩阵维度及其含义如下
- n × n n\times n n×n 对每一个输出轴进行线性变换
- ( n + 1 ) × ( n + 1 ) (n+1)\times (n+1) (n+1)×(n+1) 此时,
offset参数将不起作用,相当于把最后一个维度的参数作为偏移量 - n × ( n + 1 ) n\times (n+1) n×(n+1)
offset参数亦不起作用,但相当于最后一行的偏移量设为0。 - n n n 输入为一个向量,表示进行针对对角线的变换
下面仍以对仿射变换进行一个演示
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import *ori = np.eye(20)
ori[10, :] = 1.0a,b = 0.9,1.1
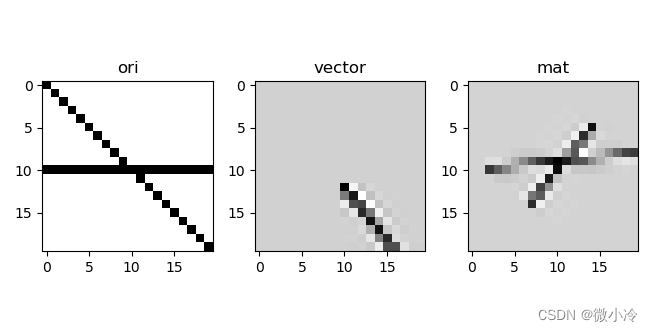
fDct = {"ori" : ori,"vector" : affine_transform(ori, [a, b], offset=(-10,-10)),"mat" : affine_transform(ori, [[a, b],[-b, a]], offset=(-10,10)),
}fig = plt.figure()
for i, key in enumerate(fDct):fig.add_subplot(1, 3, i+1)plt.imshow(fDct[key], cmap='gray_r')plt.title(key)plt.show()
效果如下