当前位置：首页 > news >正文

kruscal重构树

news 2025/7/29 9:46:49

构造：

把最小生成树上的边从小到大取出来。

这一步在实现上相当于边做 Kruskal 边构造重构树。

利用这个性质，我们可以找到到点 x 的简单路径上的边最大权值的最小值 ≤val 的所有点 y。可以发现都在 Kruskal 重构树上的某一棵子树内，且恰好为该子树的所有叶节点。

设这条边的为 x 与 y 连边，那么我们新建节点 now，将 now 连向 x,y，将 now 的点权设为这条边的边权，x 与 y 之间不连边。注意这里向 x 连边实际上指的是向 x 所在子树的根节点连边。
建完最小生成树之后，重构树也就建好了。
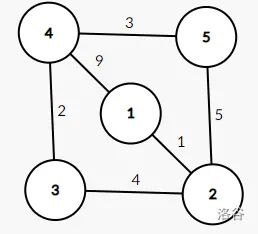
这是一张无向带权图。
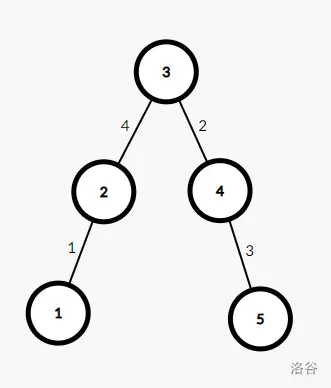
这是这张图的最小生成树。

我们将每条边从小到大建立 Kruskal 重构树。
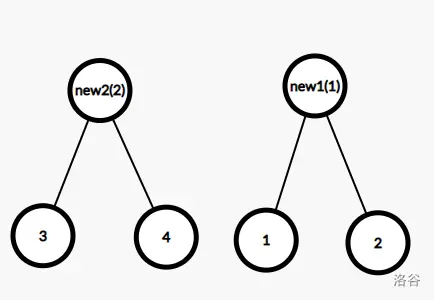
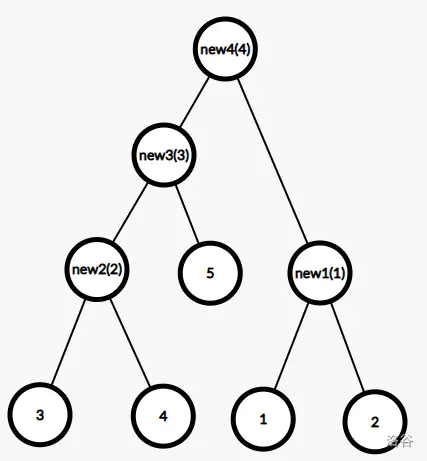
这样我们就建好了这个图的 Kruskal 重构树。

//kruscal重构树int idx = n;for(auto &[x,y,w]:edge){int fx = root(x);int fy = root(y);if(fx != fy){idx ++ ;pre[fx] = pre[fy] = idx;val[idx] = w;g[idx].push_back(fx);g[idx].push_back(fy);if(idx == 2 * n - 1)break;}}

性质：

是一棵二叉树。
如果是按最小生成树建立的话是一个大根堆。
强大性质：原图中两个点间所有路径上的边最大权值的最小值 = 最小生成树上两点简单路径的边最大权值 = Kruskal 重构树上两点 LCA 的点权。

例题：

1706E - Qpwoeirut and Vertices

我们将这条边的编号定义为它的边权。通过 Kruskal 生成树算法，连边时断开这条边，而是新建一个点，让这个新点来连接两点，新点的点权为原来连边的权值。这就是 Kruskal 重构树。

得到 Kruskal 重构树后，为了 u 和 v 连通，连接的边的最大值的最小值，即为 u 和 v 的最近公共祖先的点权。通过倍增法求出最近公共祖先即可。

对于所有的 i(1≤i<n)，我们可以先求出使 i 和 i+1 连通的代价（设为 ansi）。然后，建造线段树，预处理出区间最大值。

最后，询问 l,r 本质上就是使 [l,1+1],[l+1,l+2],…[r−1,r] 都连通，那么答案就是 maxi=lr−1ansi。利用线段树求出即可。

代码：

#pragma GCC optimize(2,"Ofast","inline")
#include <bits/stdc++.h>#define int long long
#define double long double
#define ull unsigned long long
#define fi first 
#define se second
#define ls(p) p<<1
#define rs(p) (p<<1)|1
#define YES cout<<"YES\n"
#define NO cout<<"NO\n"
#define Yes cout<<"Yes\n"
#define No cout<<"No\n"
#define sp(x) fixed << setprecision(x)
#define all(v) v.begin(),v.end()using namespace std;
mt19937_64 rng(chrono::steady_clock::now().time_since_epoch().count());
ull rnd() { return (unsigned long long)rng(); }const int inf = 0x3f3f3f3f3f3f3f3f;
const int N = 1e6 + 5;
int n,m,q;
vector<int>g[N];
struct node{int x,y,w;bool operator<(const node &u)const{return w < u.w;}
};
vector<node>edge;
int pre[N];
int val[N];//点权
int fa[N][24],dep[N];
int tr[N];
int b[N];int root(int x){return pre[x] = (pre[x] == x) ? x : root(pre[x]);
}void init(){edge.clear();for(int i=1;i<=n*2LL;i++){dep[i] = 0;g[i].clear();pre[i] = i;for(int j=1;j<=20;j++)fa[i][j] = 0;}return;
}void dfs(int x,int p){//p为父亲dep[x]=dep[p]+1;fa[x][0]=p;for(int i=1;i<=20;i++){fa[x][i]=fa[fa[x][i-1]][i-1];}for(const auto &y:g[x]){if(y==p)continue;dfs(y,x);}
}int lca(int x,int y){if(dep[x]<dep[y])swap(x,y);for(int i=20;i>=0;i--){if(dep[fa[x][i]]>=dep[y])x=fa[x][i];}if(x==y)return x;for(int i=20;i>=0;i--){if(fa[x][i]!=fa[y][i]){x=fa[x][i];y=fa[y][i];}}return fa[x][0];
}void push_up(int p){tr[p] = max(tr[ls(p)] , tr[rs(p)]);return;
}void build(int p,int l,int r){if(l == r){tr[p] = b[l];return;}int mid = l+r>>1;build(ls(p) , l , mid);build(rs(p) , mid + 1 , r);push_up(p);return;
}int query(int p,int l,int r,int nl,int nr){if(nl <= l && r <= nr){return tr[p];}int mid = l+r>>1;int res = 0;if(nl <= mid)res = max(res , query(ls(p) , l , mid , nl , nr));if(nr > mid)res = max(res , query(rs(p) , mid + 1 , r , nl , nr));return res;
}void solve(){cin>>n>>m>>q;init();for(int i=1;i<=m;i++){int x,y;cin>>x>>y;int w = i;edge.push_back({x , y , w});}sort(all(edge));//kruscal重构树int idx = n;for(auto &[x,y,w]:edge){int fx = root(x);int fy = root(y);if(fx != fy){idx ++ ;pre[fx] = pre[fy] = idx;val[idx] = w;g[idx].push_back(fx);g[idx].push_back(fy);if(idx == 2 * n - 1)break;}}dfs(idx , 0);for(int i=1;i<n;i++){int p = lca(i , i + 1);b[i] = val[p];}build(1 , 1 , n - 1);while(q--){int l,r;cin>>l>>r;if(l == r){cout<<0<<" ";continue;}cout<<query(1 , 1 , n - 1 , l , r - 1)<<" ";}cout<<"\n";return;}signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);time_t Start = clock();int T = 1;cin >> T;while (T -- ){solve();}time_t End = clock(); time_t Run_time = End - Start;//cout<<"\n"<<Run_time<<"ms"<<"\n"; return 0;
}

查看全文

http://www.lryc.cn/news/602593.html