当前位置：首页 > news >正文

欧拉图与欧拉回路

news 2025/7/28 7:33:34

欧拉路问题

先介绍一下是欧拉路相关的概念，以下概念不仅仅针对无向图。

定义

欧拉回路 ：通过图中每条边恰好一次的回路
欧拉通路 ：通过图中每条边恰好一次的通路
欧拉图 ：具有欧拉回路的图
半欧拉图 ：具有欧拉通路但不具有欧拉回路的图

性质

欧拉图中所有顶点的度数都是偶数。

若 GG 是欧拉图，则它为若干个环的并，且每条边被包含在奇数个环内。

判别法

无向图是欧拉图当且仅当：
- 非零度顶点是连通的
- 顶点的度数都是偶数
无向图是半欧拉图当且仅当：
- 非零度顶点是连通的
- 恰有 2 个奇度顶点
有向图是欧拉图当且仅当：
- 非零度顶点是强连通的
- 每个顶点的入度和出度相等
有向图是半欧拉图当且仅当：
- 非零度顶点是弱连通的
- 至多一个顶点的出度与入度之差为 1
- 至多一个顶点的入度与出度之差为 1
- 其他顶点的入度和出度相等

求欧拉回路

在判定无向图存在欧拉回路后，我们可以借助深度优先遍历和栈，求出欧拉回路的一种具体方案。流程如下：

void dfs(int x)for 从 x 出发的每条边(x,y)if(该边没有被访问过)把这条边标记为已访问dfs(y)把x入栈// in maindfs(1)倒序输出栈中所有节点

欧拉图每个节点度数为偶数说明：只要到达一个节点，就必定有一条尚未走过的边可以离开该点。故在上面的伪代码中，调用 dfs(1)，不断递归，每次都走到“从 xx 出发的第一条未访问的边”的另一端点 yy ，最终一定能回到节点 11 ，产生一条回路。如下图 a 所示：

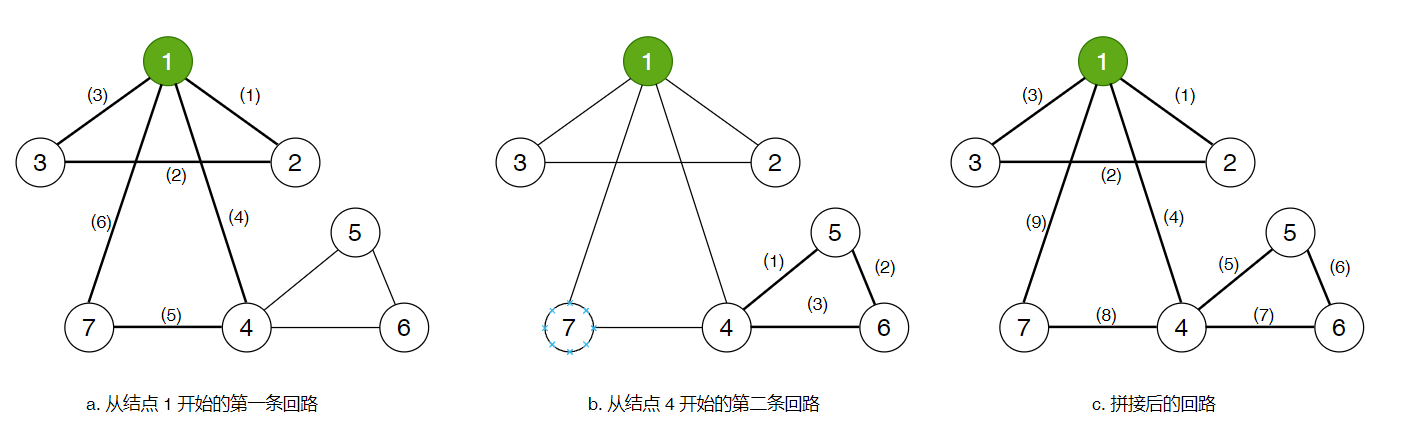
当然这条回路不能保证经过了图中的每条边。所以 dfs 函数会继续考虑从出发的其他未访问的边，找到第二条回路（如上图b 所示）。上述伪代码实际上找出了若干条回路。我们需要把这些回路按适当的方法拼接在一起，形成整张图的欧拉回路。一个很显然的拼接方法就是把第二条回路嵌入第一条回路中间（如上图 c 所示）。

上面伪代码中维护的栈，恰好替我们完成了这个拼接工作。最后，把栈里的所有结点倒序输出，就得到了一条欧拉回路。

值得提醒的是，上述算法的时间复杂度为 O(NM)O(NM) 。因为一个点会被重复遍历多次每次都会扫描与它相连的所有的边一一虽然我们明明知道大部分边已经访问过了。假设我们采用邻接表存储无向图，我们可以在访问一条边 (x,y)(x,y) 后，及时修改表头 head[x]head[x] ，令它指向下一条边。这样我们每次只需取出 head[x]head[x] ，就自然跳过了所有已经访问过的边。

另外，因为欧拉回路 DFS 的递归层数是 O(M)O(M) 级别，容易造成系统栈溢出。我们可以用另一个栈，模拟机器的递归过程，把代码转化为非递归实现。加入上述优化后的完整程序如下，其时间复杂度为 O(N+M)O(N+M) 。

模板题： P4790 USACO2005JAN Watchcow S 看门牛 - TopsCoding

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+5, M = 5e4+5;
int head[N], ver[M*2], nxt[M*2], vis[M*2], tot = 1;
int n, m;
int path[M], num;
void add(int u,int v)
{ver[++tot] = v;nxt[tot] = head[u];head[u] = tot;
}
void dfs(int u) {for(int i=head[u]; i; i=nxt[i]){int v = ver[i];if(!vis[i]) { // 这条边没访问过vis[i] = 1;dfs(v);}}path[++num] = u;
}
int main()
{cin >> n >> m;tot = 1;for(int i = 1, u, v; i <= m; i++) {cin >> u >> v;add(u, v); add(v, u);}dfs(1);for(int i = 1; i <= num; i++)cout << path[i] << '\n';return 0;
}

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+5, M = 5e4+5;
int head[N], ver[M*2], nxt[M*2], vis[M*2], tot = 1;
int n, m;
int path[M*2], num; // 路径栈
int stk[M*2], top;  // 手写栈
void add(int u,int v)
{ver[++tot] = v;nxt[tot] = head[u];head[u] = tot;
}
void dfs(int u) {for(int i=head[u]; i; i=nxt[i]){int v = ver[i];if(!vis[i]) { // 这条边没访问过vis[i] = 1;dfs(v);}}path[++num] = u;
}
void euler(int u) {stk[++top] = u;while(top) {int u = stk[top], i = head[u];// 找到一条尚未访问的边while(i && vis[i]) i = nxt[i];// 沿着该边模拟递归，标记，并更新表头if(i) {stk[++top] = ver[i];vis[i] = true;head[u] = nxt[i];} else { // u 相连的所有边均已访问，模拟回溯过程，并记在答案栈中top--;path[++num] = u;}}}
int main()
{cin >> n >> m;for(int i = 1, u, v; i <= m; i++) {cin >> u >> v;add(u, v); add(v, u);}euler(1);for(int i = 1; i <= num; i++)cout << path[i] << '\n';return 0;
}