C语言————原码 补码 反码 (超绝详细解释)
本文的内容通下面这篇文章有着紧密的联系,读者可以选择性阅读
C语言————二、八、十、十六进制的相互转换-CSDN博客
相关的C语言练习题可以参考一下文章
C语言————练习题册(答案版)-CSDN博客
目录
基本概念
原码 反码 补码 转换
数据的存储方式
基本存储单位
数据的计算方式
补码的模运算原理
移位操作符
左移操作符
右移操作符
位操作符:&、|、^、~
&的运算规则
|的运算规则
^的运算规则
~的运算规则
基本概念
我们知道不同进制的数字,归根结底都是一个个不同的表现形式 。
原码、补码和反码是整数类型在计算机内部以二进制存储时的三种不同表现形式,虽然整数具有这三种类型的存储方式,但是在内存中以补码的形式进行存储。
有符号整数在这三种方法中均由符号位和数值位两部分组成,在二进制序列中,最高的一位被视为符号位,其余都是数值位。
下面我们对这三种方式进行逐一介绍:
原码:直接将数字按照二进制转换方法得到的就是原码
反码:符号位不变,其余位依次取反得到的就是反码
补码:反码+1得到的就是补码
注:知道一个负整数的补码或者反码,想求这个负整数的值,那么应该将补码或者反码逆推回去得到原码,再由原码进行计算得到的值才是正确的,在计算中,符号位不参与权重,仅用以判断正负。
正整数的原码、反码、补码都相同;
原码 反码 补码 转换
负整数的原码、反码、补码有如下的转换形式(转换中符号位不变):
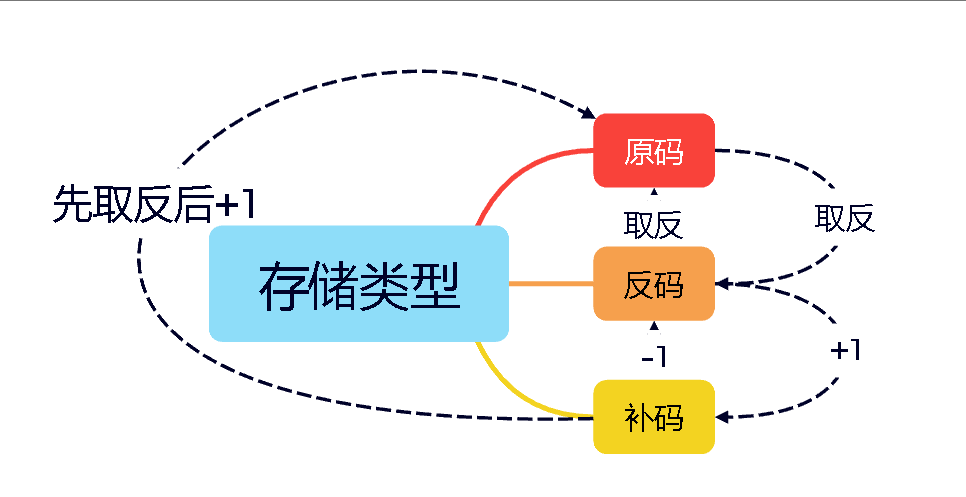
在对这三种形式运用的深入之前,我们先进行一个前置的知识储备。
数据的存储方式
我们知道,计算机内部采用二进制存储所有数据,原因是电子元件(如晶体管)的 “导通” 与 “截止” 两种状态可直接对应二进制的 “1” 和 “0”,物理实现简单且稳定。
基本存储单位
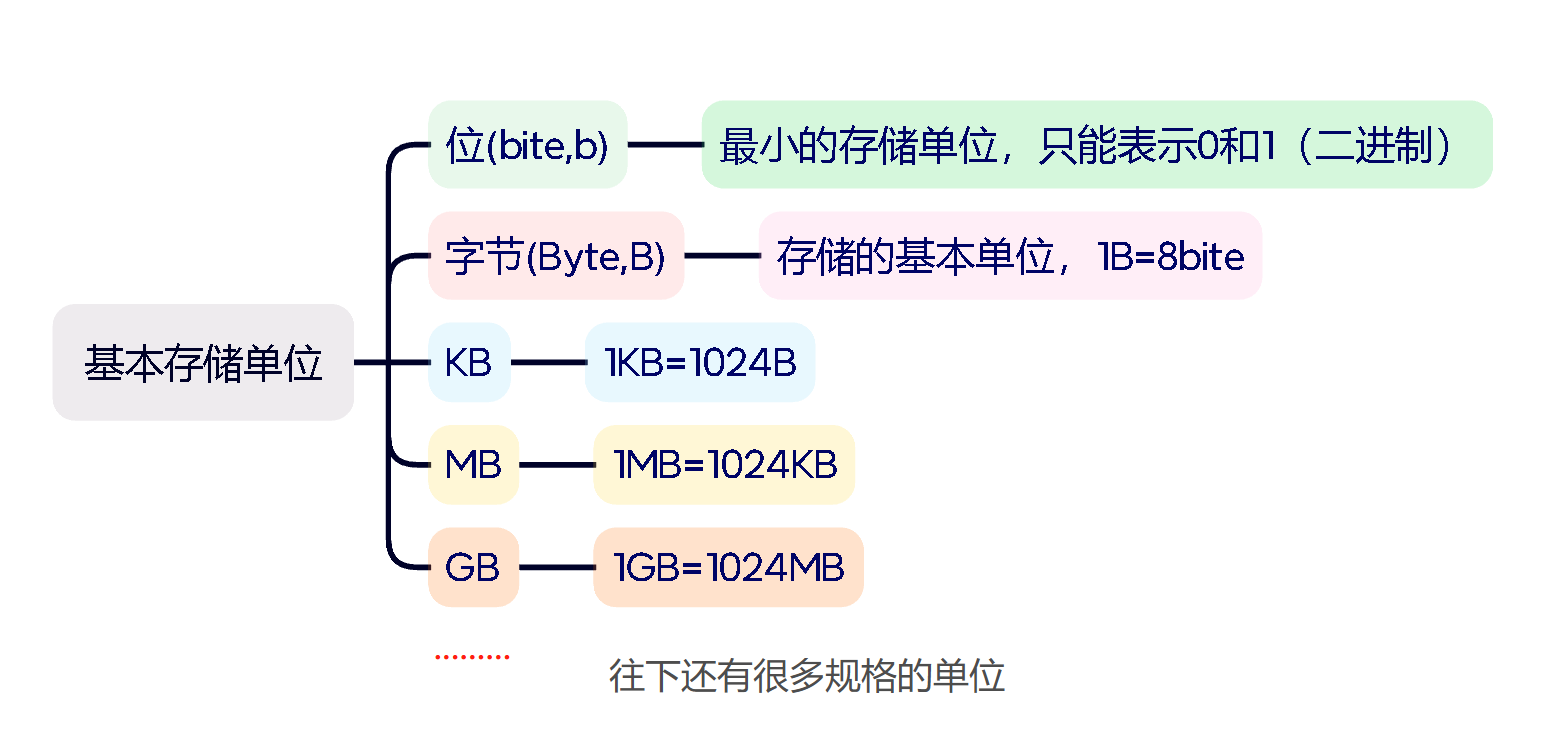
我们知道一个int的字节大小为4,那么他的二进制位数为32位,接下来我们会用int来介绍三种码之间的运用方式。
数据的计算方式
在计算机中,数据的计算和存储都是通过补码来完成的。这是因为使用补码可以对符号位和数值域进行统一的处理,同时加减法也可以进行统一处理(CPU处理器只有加法器),此外,原码和补码的相互转换,二者的方式是相同的,也不需要额外的电子元件。
那为什么使用补码而不是原码呢?
原码是利用最高位表示符号(0 代表正数,1 代表负数),其余位表示数值的绝对值。不过,原码在进行加减法运算时会碰到一些难题:
- 符号位处理复杂:在进行加减法运算时,需要先判断操作数的符号,然后再决定是进行加法还是减法运算。
- 存在正负零:原码中存在两种零的表示方式,即
+0(0000)和-0(1000),这会使比较操作变得复杂。 - 减法运算困难:当进行减法运算时,需要设计专门的电路来执行减法操作,这增加了硬件的复杂度。
补码是通过对原码取反后加 1 得到的,它成功解决了原码存在的上述问题。
- 统一加减法运算:在补码系统中,减法可以转换为加法来进行计算,比如
A - B可以表示为A + (-B)。这样一来,计算机就不需要设计专门的减法电路,只需一个加法器就能完成加减法运算。 - 消除正负零:在补码表示中,零只有一种表示形式,即
0000。而1000则被用来表示-8,这使得数值的表示范围得到了扩展。(+0和-0的补码结果时一致的,所以只有一种表示形式) - 简化硬件设计:由于加减法运算可以统一用加法器来实现,硬件设计变得更加简单,同时还能减少出错的概率。
int main() {//1 - 1//1 + (-1)//00000000000000000000000000000001 ---- 1的原码//00000000000000000000000000000001 ---- 1的补码//00000000000000000000000000000001 ---- 1的反码//10000000000000000000000000000001 ---- -1的原码//11111111111111111111111111111110 ---- -1的反码//11111111111111111111111111111111 ---- -1的补码//那么我们用原码进行计算时我们可以得到值为10000000000000000000000000000010 即-2,与结果不符//我们使用补码进行计算时可以得到00000000000000000000000000000000 即0,数值相符return 0; }通过上述代码,我们发现,使用原码进行计算时(相当于没有考虑正负符号直接求和),得到的结果与值不符,而补码计算时完美的弥补了他的不足。
补码的模运算原理
补码其实是一种模运算系统。对于 n 位二进制数,其模为 2ⁿ。例如,4 位二进制数的模就是 16。在模运算中,减去一个数就相当于加上这个数的补数,即x - y ≡ x + (2ⁿ - y) (mod 2ⁿ)。
以 4 位二进制数计算5 - 3为例:
-
可以转化为
5 + (-3) -
-3的补码为1101(也就是16 - 3 = 13) -
计算
5 + 13 = 18,由于模为 16,18 mod 16 = 2,结果正确。
另,整数值和其补码对应的值由如下对应关系:
-
正数:直接表示为二进制,范围是
0到2^(n-1)-1。 -
负数:
-N表示为2^n - N,范围是-2^(n-1)到-1。例如,4 位补码的模是
16: -
-5表示为16 - 5 = 11(二进制1011)。{取反+1得到1101即-5} -
-8表示为16 - 8 = 8(二进制1000)。{取反+1得到0000,这是错误的示范,8在4位二进制无法用原码表示,进一步体现了原码的局限性}
移位操作符
<< 为左移位操作符
>> 为右移位操作符
注:他们的操作数都只能是整数,有且仅有两个操作数,只能移动非负数位
左移操作符
移动规则:左边抛弃,右边补0
对于 10 << 1 ,他的具体变化如下:

#include <stdio.h>
int main()
{int num = 10;int n = num<<1;printf("n= %d\n", n);//变成20printf("num= %d\n", num);//num不变,即不改变num自身的值return 0;
}右移操作符
右移操作符具有两种不同的移动规则:
1.算术右移:左边用原该值的符号位填充,右边丢弃
2.逻辑右移:左边用0填充,右边丢弃
对于-10 >> 1,采用算术右移变化如下:
对于-10 >> 1,采用逻辑右移变化如下:
#include <stdio.h>
int main()
{int num = -10;int n = num>>1;printf("n= %d\n", n);//变成-5printf("num= %d\n", num);//num不变,即不改变num自身的值return 0;
}在实际运算中,>>右移操作符采用算术右移还是逻辑右移,取决于编辑器规则;但一般情况下采用的是算术右移。
位操作符:&、|、^、~
位操作符有:
&的运算规则
|的运算规则
以两个整数的补码进行计算,对应的二进制位上,有1就为1,同时为0才为0。
^的运算规则
以两个整数的补码进行计算,对应的二进制位上,相同为0,相异为1。
~的运算规则
根据取反的规则,对整数的补码进行取反运算。
———————————————————————————————————————————
后续会更新针对于二进制数的相关操作符
有表述不当的地方辛苦大家指出,三克油。
打怪升级中................................................................................................................................................
