最大团--贪心例题
1.题目
2.思路分析
这是一个图论(可能是,主播还没学,瞎说的)和贪心的结合体,整个题的核心在于这个公式abs(xi-xj)>=wi+wj,首先我们先假设按x值进行了排序(之所以在代码中没有体现,是因为在这里排好序之后后面的sort函数会再次进行排序,这次的排序的意义就会消失,所以只是假设就可以,不影响最终结果),得出xj>=xi.
然后我们进行合并同类项,得出xj-wj>=xi+wi
在这里需要注意一个点”最大团“指的是所有不重叠的点,不一定要连续。根据这个我们来推导三个点x1<=x2<=x3的关系。若x1和x2有边,则应有x2-w2>=x1+w1;若x2和x3有边,则应有x3-w3>=x2+w2;然后我们根据这两条信息推导x1和x3的关系:x1+w1<=x2-w2<=x2+w2<=x3-w3;即x1+w1<=x3-w3;说明x1和x3也有边。
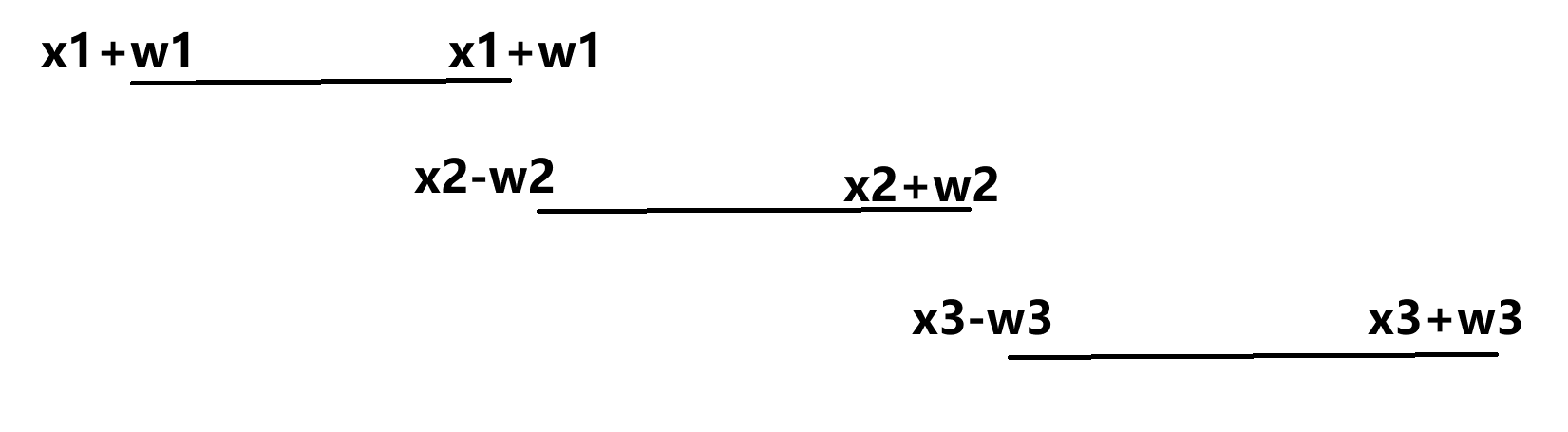
把每个点的信息画成线段,左端点是x-w,右端点是x+w。问题建模为:在n个线段中找出最多的线段,是他们互相不交叉(不交叉即满足题目给出的那个公式)。若是读者学过我之前所说的 不相交区间问题 ,会发现这个题可以转化为在n个活动中安排尽量多的活动,是他们互相不冲突。他的贪心解法如下:
1.按活动的结束时间排序。本题按x+w排序。
2.选择第一个结束的活动,跳过与他时间冲突的活动。
3.重复第二步,直到活动为空。每次选择剩下活动中最早结束的活动,并跳过与他冲突的活动。
下面代码的时间复杂度:排序为nlog2n,贪心为n,总体是nlog2n
3.代码呈现
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 200010;
struct aa { long long l, r; }a[N];
bool cmp(aa a, aa b)
{return a.r < b.r;
}
int main()
{int n;cin >> n;int x, w;for (int i = 0; i < n; i++){cin >> x >> w;a[i].l = x - w;a[i].r = x + w;}sort(a,a+n,cmp);long long R = a[0].r;int ans = 1;//临时答案for (int i = 1; i < n; i++){if (a[i].l >= R){ans++;R = a[i].r;}}if (ans == 1){ans = 0;}cout << ans << endl;return 0;
}