当前位置：首页 > news >正文

三维手眼标定

news 2025/7/25 11:01:59

机器视觉手眼标定

1.意义：

确定机器人工具中心点（TCP）与相机之间的固定关系

2.分类：

在实际应用中，手眼标定常有两种形式: 系统标定 和 在线标定。系统标定指的是在工厂中进行的标定过程，标定完成后在实际应用中不再需要更新；在线标定则意味着在实际运行过程中能够持续更新标定参数，以适应工作环境的改变。

3.步骤：

手眼标定过程主要包括以下步骤：

选定机器人工具中心点和对应的相机。
采集一组机器人姿态数据和相机图像信息。
利用以上采集的信息，通过优化方法或其他算法计算出相机与机器人工具中心点之间的精确位置关系。手眼标定算法也有很多，如Tsai、Horaud等。

注意：为了准确地估计这种关系，通常需要从不同的位置和姿态采集数据，以便获得充足和多样性的数据，进一步提高标定结果的精度和稳定性。数据丰富度，算法需求，减少误差，环境和姿态覆盖，验证和评估

4.误差来源

手眼标定的目标是确定相机坐标系和机器人末端执行器坐标系之间的转换关系。

特征点检测误差：
- 标定时通常使用某种模式板（例如棋盘格、圆点网格等）作为参考。如果在图像中检测这些特征点的过程中存在误差，那么这会直接影响标定的结果。
摄像机内参标定误差：
- 手眼标定的前提是相机的内参（如焦距、主点位置、径向和切向畸变等）已知。如果这些参数的标定存在误差，那么手眼标定的结果也会受到影响。
机器人位置误差：
- 机器人的位置和姿态信息通常由编码器提供。任何与机器人的精度和重复定位精度相关的误差都会影响手眼标定。
机械误差：
- 机器人的关节间隙、伸缩、弯曲或其他机械误差都会影响标定结果。
测量噪声：
- 无论是图像采集还是机器人位置的测量，都可能受到系统噪声的影响。
模式板制造和安装误差：
- 如果模式板的制造不精确或在安装过程中发生变形，都可能导致标定误差。
算法和数值计算误差：
- 手眼标定算法的选择和实现、以及在解决标定问题时使用的数值方法，都可能引入误差。
环境因素：
- 温度、湿度、照明条件等都可能影响摄像机成像和机器人的精度。
系统时延：
- 如果机器人和相机之间的数据同步存在延迟，这也可能影响标定结果。
模型简化：

在手眼标定中，常常使用某些简化的数学模型。这些模型可能无法完全捕获实际系统的全部复杂性，从而引入误差。

为了最小化这些误差，通常需要多次标定和验证，选择合适的标定算法，并确保所有设备和标定工具的质量。

5.标定原理

手眼标定主要是为了确定机器人手部（通常是机械臂的末端）和相机之间的固定关系。标准的问题可以表示为下面的等式： [ AX = XB ]

其中：

( A ) 是机器人从一个位置到另一个位置的变换矩阵。
( B ) 是相机在这两个位置所观测到的模式板的变换矩阵。
( X ) 就是我们要找的机器人手部到相机的变换矩阵。

描述过程：

机器人移动其手部从位置1到位置2。
在这两个位置，相机分别捕获模式板的图像，并计算模式板的位置和姿态。
根据这两个位置，可以计算机器人手部和相机观测到的模式板之间的变换矩阵，即 ( A ) 和 ( B )。
使用多次观测，可以解决上述的 ( AX = XB ) 问题，从而找到 ( X )。

这只是一个基本的描述。为了更清楚地表示这一过程，您可能需要绘制机器人、相机、模式板以及它们之间的关系，同时注明相关的变换矩阵。

5.1 眼在手上

相机安装在机械手上，相机随着机械手一起移动。实际工程上较为常用。
可以快速有效地标定被测物体的坐标。这种情况的标定过程实际上和相机和机械手分离的标定方法是一样的，因为相机拍照时，机械手会运动到相机标定的时候的位置，然后相机拍照，得到目标的坐标，再控制机械手，所以简单的相机固定在末端的手眼系统很多都是采用这种方法，标定的过程和手眼分离系统的标定是可以相同对待的。

基于图像的视觉控制
基于位置的视觉控制
结合两者的混合视觉控制

5.2 眼在手外

相机固定在机器上，机械手的运动不会带着相机一起移动。

5.3 数学推导

参考手眼标定_全面细致的推导过程_12点标定-CSDN博客

上文的相机搭载方案是，hand-in-eye。移动相机，标定求解过程
在推导过程中，我们会用到四个坐标系，分别是：

下面先给出示意图：

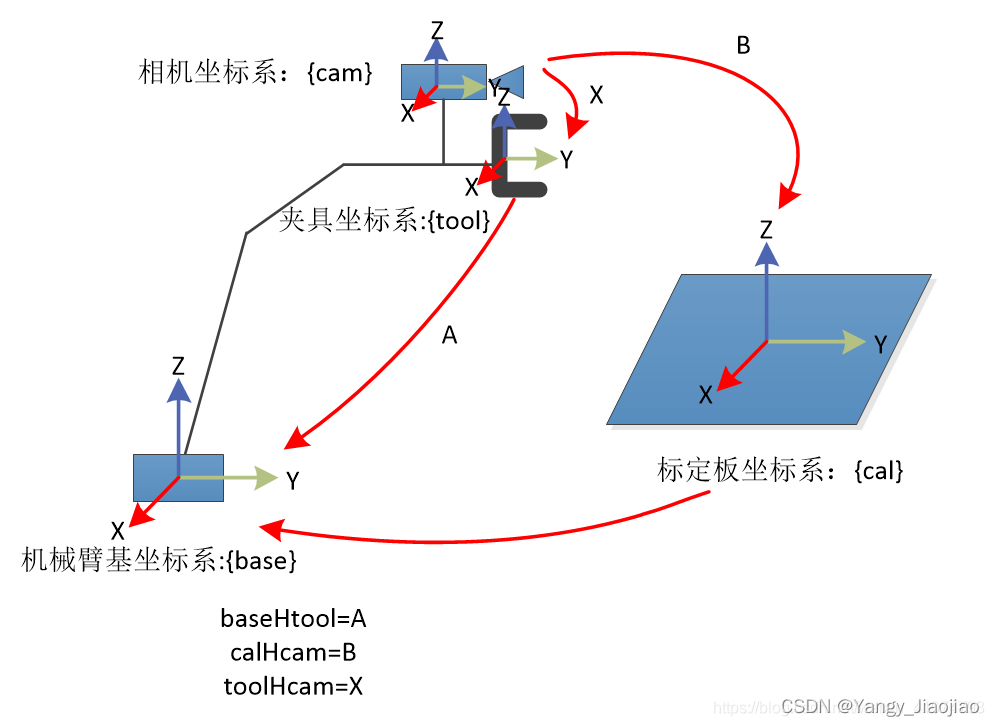
基础坐标系（用base表示）
机械手坐标系（用tool表示）
相机坐标系（用cam表示）
标定物坐标系（用cal表示）

5.4 仿射变换矩阵

理解：求两个坐标系之间的关系，就是通过三个旋转和三个平移得到一个变换矩阵。

三个旋转和三个平移来表示，通常使用仿射变换矩阵来表示这种变换。这种矩阵通常被称为变换矩阵或变换矩阵。

假设你有两个坐标系，我们称它们为"源坐标系"和"目标坐标系"，它们之间的变换可以表示为以下形式的仿射变换矩阵：

| a  b  tx |
| c  d  ty |
| 0  0  1  |

其中 a 和 d 是缩放因子，b 和 c 是旋转因子，tx 和 ty 是平移因子。这些因子可以通过旋转角度、缩放比例和平移向量来确定。

相机得到的是 像素坐标，机械手是空间坐标系，所以手眼标定就是得到像素坐标系和空间机械手坐标系的坐标转化关系。
在实际控制中，相机检测到目标在图像中的像素位置后，通过标定好的坐标转换矩阵将相机的像素坐标变换到机械手的空间坐标系中，然后根据机械手坐标系计算出各个电机该如何运动，从而控制机械手到达指定位置。这个过程中涉及到了图像标定，图像处理，运动学正逆解，手眼标定等。

6.标定流程

手眼标定的流程大致可以分为以下步骤：

系统准备： 配置您的机器人和相机系统，确保它们可以同步运行，并且相机可以正确地观测到目标（通常是模式板）。
数据采集： 移动机器人手部到不同的位置，每次移动时，同时记录机器人手部的位置（从机器人的编码器或其他传感器获得）以及相机视野中的模式板的图像。
特征提取： 对每一帧图像，通过某种算法（例如，对于棋盘格模式板，通常可以使用OpenCV中的函数）找出模式板的位置和姿态。
变换矩阵计算： 对于相机，可以基于提取到的特征以及相机的内参，计算出模式板的变换矩阵；对于机器人，其变换矩阵可以直接由手部的位置得到。
求解标定矩阵： 在您有一定数量（通常需要多次观测）的变换矩阵后，您可以通过解AX=XB这个单应性矩阵束平差问题得到相机和机器人手部之间的固定变换矩阵。
验证标定结果： 在获取标定结果后，应验证其准确性。这通常可以通过再次运动机器人到不同的位置，并计算由标定结果预测的模式板的位置和姿态与由相机直接测量的值之间的误差来实现。如果误差在可接受范围内，则标定过程完成；否则，可能需要重新标定或调试您的系统。