当前位置：首页 > news >正文

暑假算法训练.6

news 2025/7/23 6:34:34

27. 一维前缀和模板：

27.1 题目解析：

27.2 算法思路：

27.3 代码演示：

编辑

27.4 总结反思

28. 二维前缀和模板：

28.1 题目解析：

28.2 算法思路：

28.3 代码演示：

编辑

28.4 总结反思：

29 力扣 724.寻找数组的中心下标

29.1 题目解析：

29.2 算法思路;

29.3 代码演示：

29.4 总结反思：

30. 力扣238.除自身外数组的乘积

30.1 题目解析：

30.2 算法思路：

30.3 代码演示：

编辑

30.4 总结反思：

31.力扣 560.和为k的子数组

31.1 题目解析：

31.2 算法思路：

31.3 代码演示：

编辑

31.4 总结反思：

27. 一维前缀和模板：

27.1 题目解析：

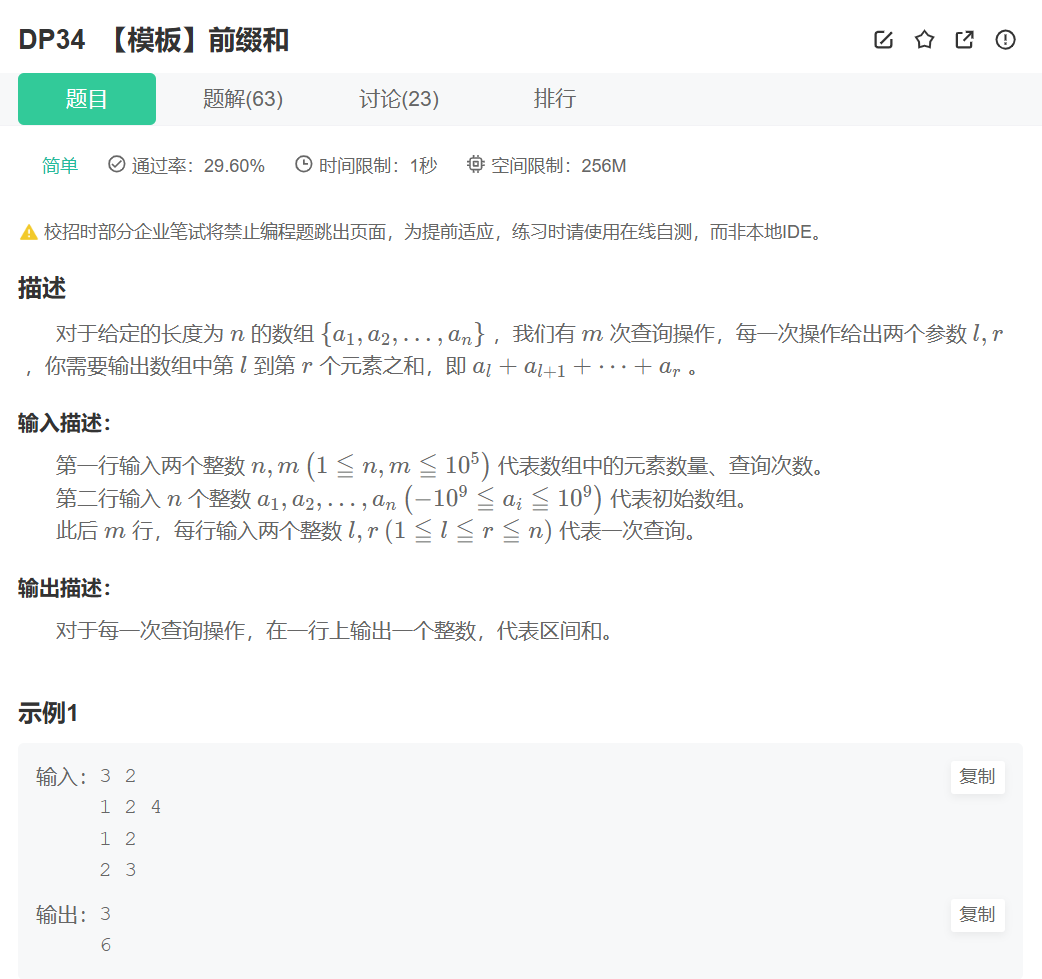
题目大家仔细的阅读一下，就可以很好的理解了。那么咱们主要来讲一下前缀和算法：就是可以快速求出数组中某一个连续的区间的的和。

27.2 算法思路：

算法就是使用前缀和去做。

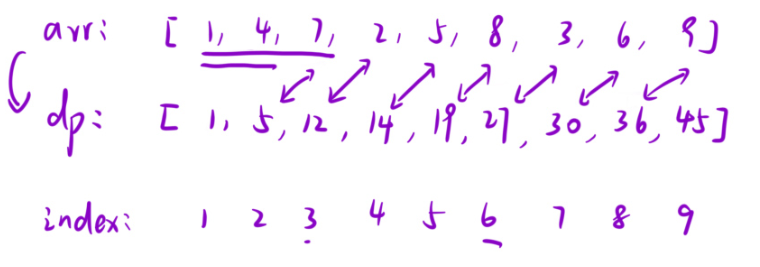
那么这个图片上的什么意思呢？

好，通过看这个是不是就了解了第一张图片什么意思，就是创造了一个前缀和数组。然后前缀和数组如何求的呢？就是用到了第二张图片的第二个公式。

现在到了第二步，就是使用前缀和数组：

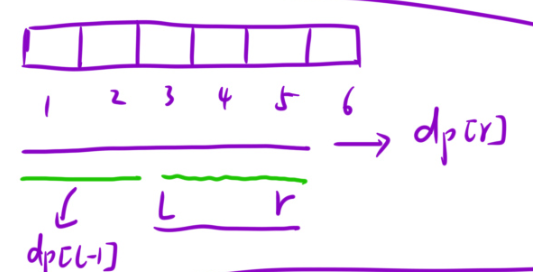
咱们要求一个区间，l与r之间的区间的和，是不是直接就可以使用前缀和数组相减不就可以了吗？

dp[l-1]是0到l-1内的和（因为咱们要求的是l到r的和，所以l也得算上）。

那么咱们再来思考一个问题：就是为什么下标要从1开始呢？其实呢，是因为避免处理边界情况，假设下标从0开始，那么：

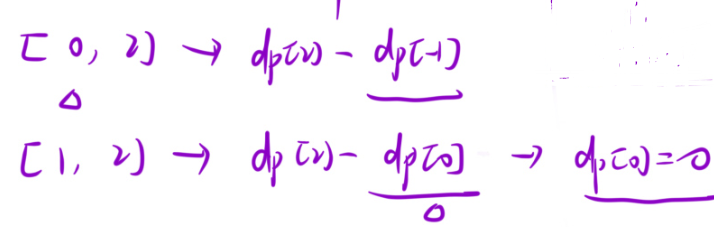
dp[-1]不是就越界了嘛？以及还要令dp[0]=0才可以。否则，1-2区间内的和没法求。

等咱们后面学了动态规划，就知道这个是初始化：添加虚拟结点（辅助结点）。

27.3 代码演示：

int main() {//1.输入数据int n = 0; int q = 0;cin >> n >> q;vector<int> arr(n + 1);//增加n+1个位置，并初始化为0for (int i = 1; i <= n; i++) cin >> arr[i];//2.预处理前缀和数组vector<long long>dp(n + 1);//使用long long 防止溢出for (int i = 1; i <= n; i++) dp[i] = dp[i - 1] + arr[i];//3.使用前缀和数组int l = 0; int r = 0;while (q--){cin >> l >> r;cout << dp[r] - dp[l - 1] << endl;}return 0;
}

由于题目说的是1~n内的数字，所以说for的范围就是<=n.

27.4 总结反思

到了后面，这种题做的多了，会发现路子其实都是一样的。

28. 二维前缀和模板：

28.1 题目解析：

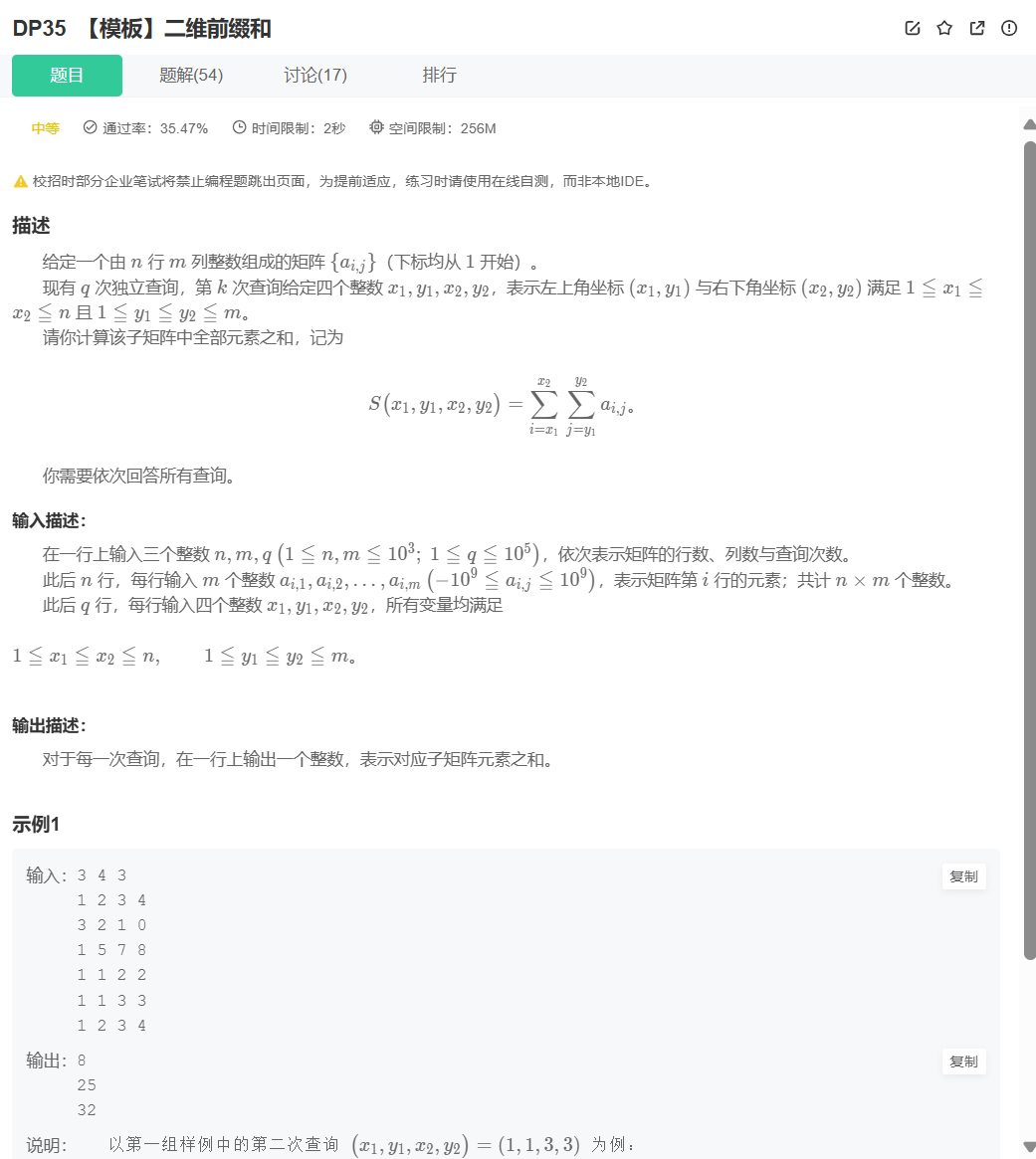题目也很好理解，就是在一维上再增加一维，就是二维。就可以了。这个有点像那个二维数组。

28.2 算法思路：

这个咱们还是使用前缀和来做。

1.预处理出来一个前缀和矩阵：

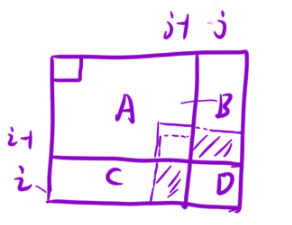
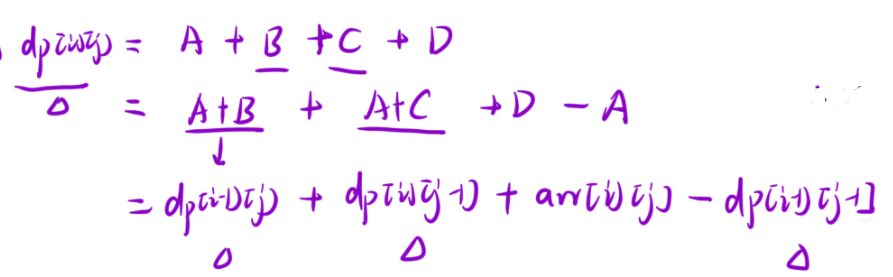
这个的求和方法有点类似于小学做的奥数题，就是求面积的。需要注意的是，本题中说的下标是从1开始的，所以说咱们的下标原数组与dp数组都是相同的下标，所以不需要纠结下标的问题。但要是下标从0开始，那么就需要好好的算一下dp后的下标了。还有就是，如果说你实在理解不了这个下标为什么这么写，你可以随机举一个例子，然后自己带进去看一看不就出来了吗？

2.使用前缀和矩阵。

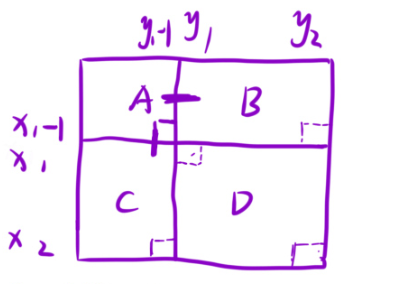
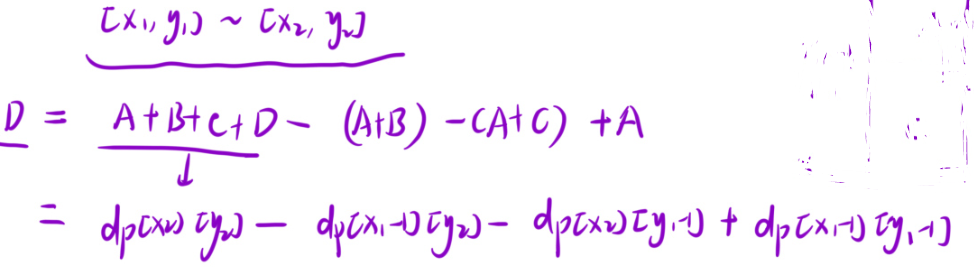
本题中人家也是下标从1开始的，很好办。还是老办法，要是实在想不明白，自己举个例子，使用下标往里面带一带，不就清楚了吗？那么咱们再来看一下如果说下标从0开始的，是怎么个计算方法：

其实博主的字比这个好看多了，只因为这是我自己的笔记，所以说我就随便写的（遵循一个自己能看懂就可以了）。

28.3 代码演示：

int main() {int n = 0; int m = 0; int q = 0;cin >> n >> m >> q;vector<vector<int>> arr(n + 1, vector<int>(m + 1));//由于下标从1开始，所以要开n+1，m+1个空间for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> arr[i][j];}}//创造前缀和数组vector<vector<long long>> dp(n + 1, vector<long long>(m + 1));for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];}}//使用前缀和数组int x1 = 0, x2 = 0, y1 = 0, y2 = 0;while (q--){cin >> x1 >> y1 >> x2 >> y2;cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] << endl;}return 0;}

28.4 总结反思：

博主也是用了很长时间才把这个给搞清楚，这个我感觉还是挺容易混的。所以大家一定要好好的看看，

29 力扣 724.寻找数组的中心下标

29.1 题目解析：

题目的意思就是找到一个数字，使得这个数字的左面的和等于右面的和，并返回这个下标。不过要注意一下例如0 0 0 这样的是返回坐左边的那个下标就可以了。

29.2 算法思路;

1.解法一肯定就是暴力解法：一个一个的枚举，这还没完，枚举完之后，枚举了一个，加一遍左边，再加一遍右边，等等，这样算下来，时间复杂度就是O(n).

2.第二种算法思路就是使用前缀和去做，不过本题需要用到前缀和加上后缀和（其实就是特殊的前缀和）。

第一步就是创造好前缀和数组：

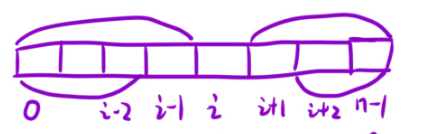
这个f[i-1]代表的是0到i-2这个范围内的和，然后再加上第i-1这个位置的数字，就是0到i-1这个区间内的和。而g[i+1]代表的是i+2到n-1范围内的和。

之后一个一个的再去枚举0~n-1内的所有的下标i，之后判断f[i]与g[i]是否相等即可。

但我们还需要注意一些边界问题：

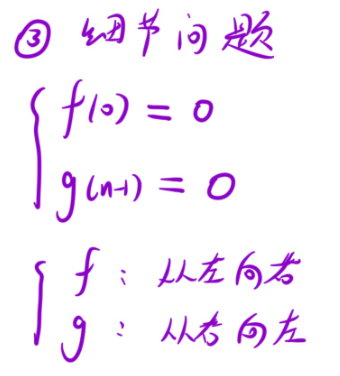
f[0]=0.是因为左边没有元素了，根据题意，那不就是0嘛。以及g[n-1]=0.右边没有元素了，所以也为0.

f是从左向右填表，是因为f[i]依赖于 f[i-1].而g从右向左填表，是因为g[i]依赖于g[i+1].

29.3 代码演示：

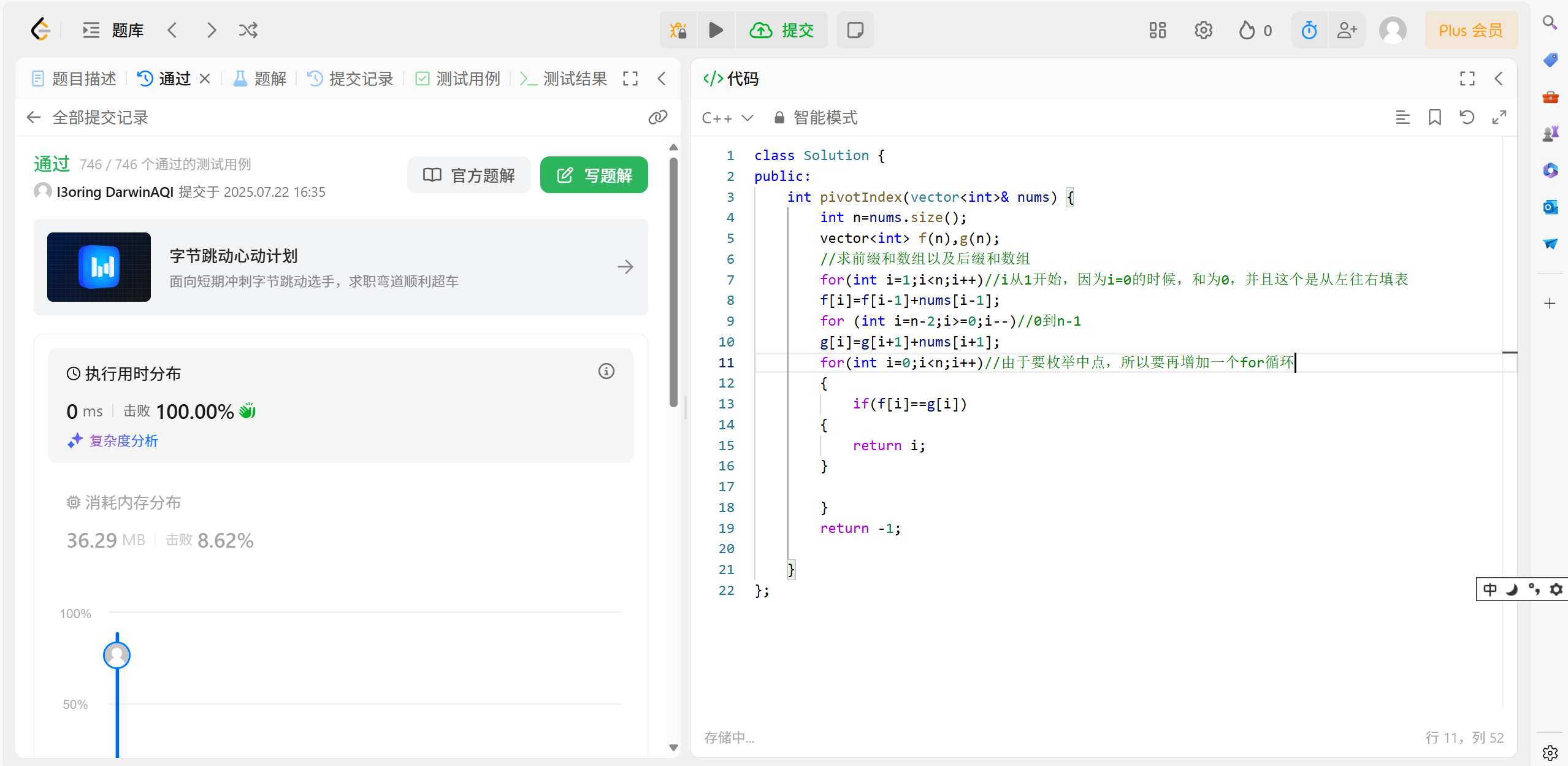
int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int> f(n), g(n);//求前缀和数组以及后缀和数组for (int i = 1; i < n; i++)//i从1开始，因为i=0的时候，和为0，并且这个是从左往右填表f[i] = f[i - 1] + nums[i - 1];for (int i = n - 2; i >= 0; i--)//0到n-1g[i] = g[i + 1] + nums[i + 1];for (int i = 0; i < n; i++)//由于要枚举中点，所以要再增加一个for循环{if (f[i] == g[i]){return i;}}return -1;}
int main()
{vector<int> nums = { 1, 7, 3, 6, 5, 6 };cout << pivotIndex(nums) << endl;return 0;
}

这里是0~n-1，所以说，i<n即可。又因为可以取到0，所以说下面的i>=0.

29.4 总结反思：

还差最后一个题，这类的做法做法的基本思路就总结出来了。

30. 力扣238.除自身外数组的乘积

30.1 题目解析：

题目很好理解，返回的数组，每一个下标的代表的那个位置，除了那个位置之外的其他地方相乘就是那个位置的值。并且还是整个数组都是这样的。说明，咱们需要再另外创建一个数组去存储才可以。

30.2 算法思路：

同样的还是使用前缀和去做，只不过这次不是前缀和，而是前缀积。

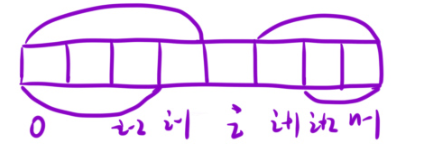
不就是除了那个位置之外的，前缀积乘上后缀积嘛？这个f[i],g[i]的公式的意义与上一题一样，这里我就不过多的阐释了。

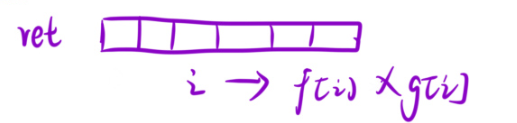
那么咱们算完之后，要创建一个数组，去返回这个成积即可。并且，这个还得是for循环，否则，无法覆盖到每一个位置。

同样需要处理一下边界条件，这里不可以再设f[0]为0了，因为0乘以任何数都为0，那这还有啥意义？

30.3 代码演示：

vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> f(n), g(n);f[0] = g[n - 1] = 1;//细节处理//预处理一下前缀和数组以及后缀和数组for (int i = 1; i < n; i++)f[i] = f[i - 1] * nums[i - 1];for (int i = n - 2; i >= 0; i--)g[i] = g[i + 1] * nums[i + 1];//使用前缀和数组以及后缀和数组vector<int> outcome(n);for (int i = 0; i < n; i++){outcome[i] = f[i] * g[i];}return outcome;
}
int main()
{vector<int> nums = { 1,2,3,4 };vector<int> outcome = productExceptSelf(nums);for (auto& e : outcome){cout << e << "";}cout << endl;return 0;
}

由于这次也是使用的0~n-1范围内的数字。所以for的范围也是那些。

30.4 总结反思：

那么咱们就来说明一下这类题目的做法，相信从前面几道题，大家已经看出来是怎么个办法了。就是先分析题目，找出方程式（创建前缀和数组），之后使用前缀和数组，算出结果。最重要的是最后要处理一下边界条件，基本都是这样的。边界条件基本就是最前面以及最后面。

31.力扣 560.和为k的子数组

31.1 题目解析：

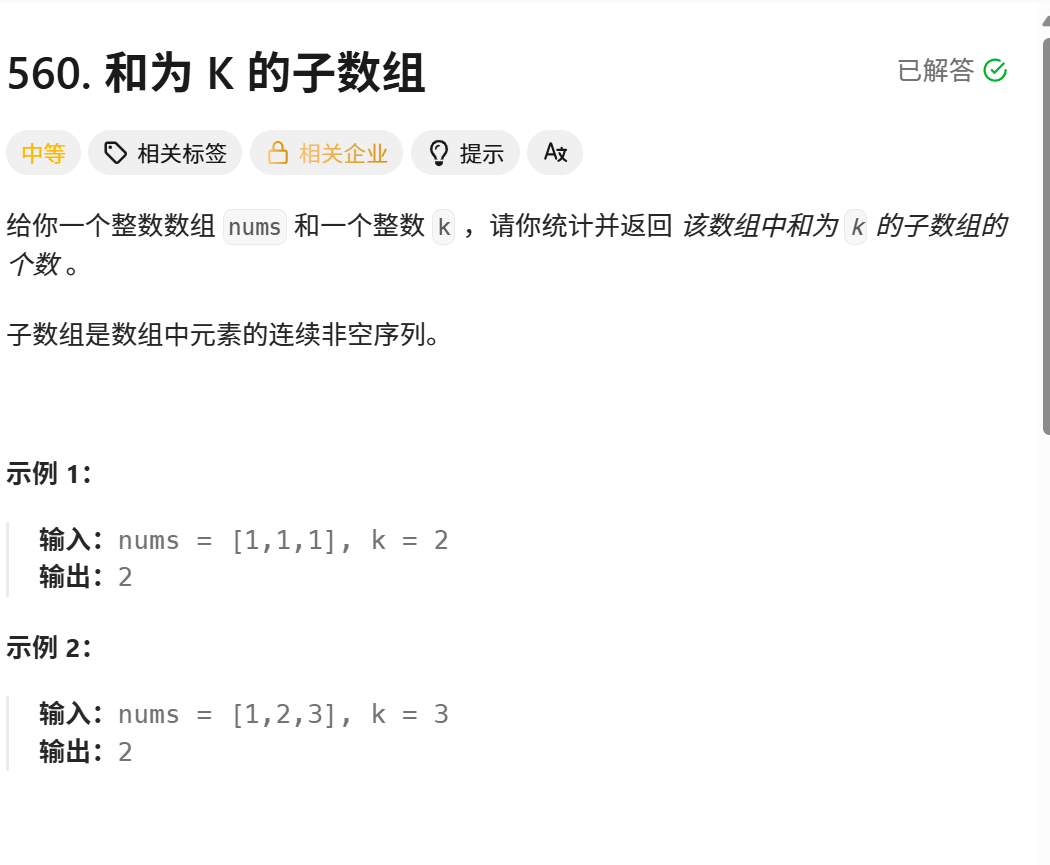
其实就是寻找子数组，那么一看到子数组，是不是就会想到咱们之前讲的双指针（滑动窗口），但其实这道题不可以使用。因为这道题包含0以及负数，咱们直到，滑动窗口，滑动的窗口里面不可以包含负数，否则就不可以使用。

31.2 算法思路：

那么既然滑动窗口不可以使用，咱们就是用前缀和加上哈希表。

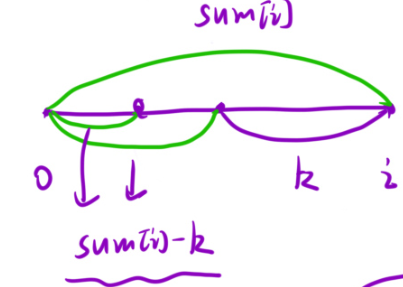
这道题咱们是不是可以转化为求sum[i]-k？是的，可以这么转化的。

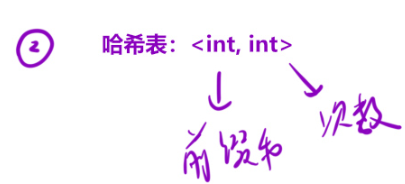
不过这里需要使用到哈希表。

、

上面是一些细节问题，大家看一下，深入理解一下。

31.3 代码演示：

int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> hash; // 统计前缀和出现的次数hash[0] = 1;int sum = 0, ret = 0;for (auto x : nums) {sum += x; // 计算当前位置的前缀和if (hash.count(sum - k))ret += hash[sum - k]; // 统计个数hash[sum]++;}return ret;
}
int main()
{vector<int> nums = { 1,1,1 };int k = 2;cout << subarraySum(nums, k) << endl;return 0;
}