高精度加法模版介绍

这个文章写一下这个高精度的加法的总结，模版，具体的操作方法，这个内容也是我第一次学习，总结一下；

关于这个叫法，其实是有很多的，比如这个高精度，大整数，之类的，都是可以的，说的都是一个东西，也就是我们的这个int类型存不下这个数据的范围，double虽然是8字节，但是这个存储的数据的范围也是有限的，因此这个需要学习一下我们的大数的加法，这个和我们的数学里面的列竖式是非常相似的，主要就是使用编程进行实现；

声明：部分图片来自于比特就业课算法竞赛课程的课件，侵权联系删除；

1.大整数加法引入

题目大概是下面的这个样子的，我从网站和这个洛谷上面找到了不同的题目，但是可以使用一样的代码实现这个大整数加法的这个流程；

下面的这个是洛谷的题目

下面的这个是船长的HZOJ的题目：

为什么这个叫做大整数加法，其实大家看看这个数据的范围就知道原因了：我随便借去了一个对应的题目的数据的范围，我们知道这个指数的量级，这个远远超出啦我们的这个Int,double等相关的这个数据类型的范围，我们的只能使用高精度的加减法；

其实在针对于这个大数的加减法的运算的时候，如果大家学习过这个Python相关的内容，你就会发现这个Python对于这个的支持其实是非常的不错的；这个就是因为我们的Python是天生的这个支持大数的相关的运算的，但是我们的这个c++里面不支持大数据的运算，需要使用特殊的手段进行相关的处理，这个也是为什么我们的python在大数据相关的这个领域非常不错的原因，这个也是老师今天告诉我们的；

但是python虽然支持这个大数据的运算，但是这个运算的效率并不是非常的显著；因此我们又必须要学习一下使用c++如何解决这类相关的问题；

2.具体说明

我们的题目就是上面的题目，其实这个题目类型很单一，这个就是纯纯考验大家有没有学过，因此这个没有啥很多的技巧；

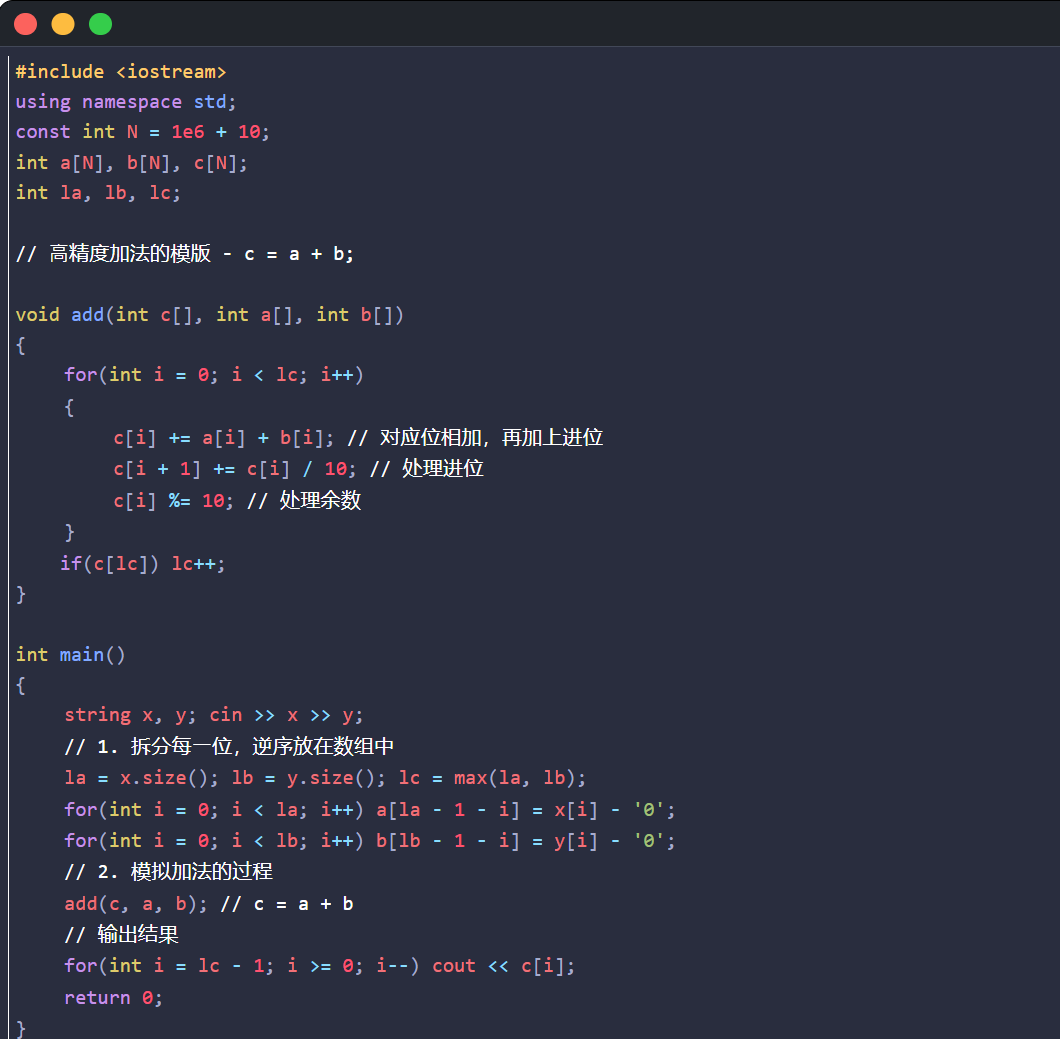
下面的这个就是我们的代码，我简单的解释一下这个思路，然后说一下自己的理解：

1）这个基本上就是我们的这类题目的模版，这个在洛谷和其他的的这个平台上面我自己都是进行了对应的测试的，都是可以运行成功的；

2）这个里面的定义的数组的数量是3个，分别存放的就是我们的第一个加数，第二个加数和我们的结果；

3）我们的这个整体的思路就是for循环里面的这个内容，对应数位上面的数据进行求和，一定是+=，这个细节大家需要注意到，因为我们的这个等于号就只会处理这个加法的加数的运算情况，但是这个+=可以处理存在这个进位的情况；

4）下面的这个是借用我们的老师的这个板书，说明一下这个n-1-i的来历，这个n就是我们的这个字符串里面的数据的个数，也可以成为这个字符串的size；

其实我们的这个大数的加法处理的时候就是当做这个字符串进行处理的，然后倒序存到我们的这个数组里面去，找到这个对应数据的下标之间的这个关系即可；

例如我们的下面的这个板书里面的439存放到我们的这个数组里面之后就是934，这个事倒序的过程，拿9来说在这个字符串里面的小标是2，在我们的这个数组里面的下标是0，因此这两个下标的求解就是0+2=2，也就是我们的3-1，这个3也就是我们的n，也就是我们的这个字符串里面的这个数据的个数，也还是我们的这个字符串的size，就是这么得来的；

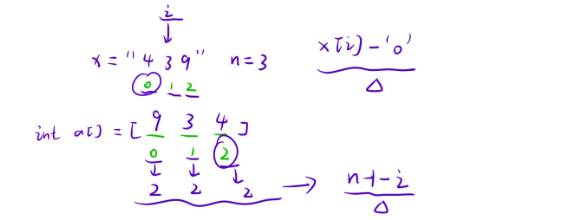
5）add方法里面的处理进位和余数就是触除法运算和取模运算；

6）在这个add；里面额外处理这个多位的情况，例如我们的999+1=1000，这个时候两个加数是3位数和1位数，但是我们的和是4位数，因此这个需要我们对于这个额外的情况进行单独的处理；

7）因为我们放到这个数组里面的时候是倒序存放的，因此这个最后计算的结果打印输出的时候也是倒序进行输出的，这个需要注意一下；

8）基本上就是这个样子吧，这个也算是我们的这个高精度加法的模版题目和代码模版