【算法题解】24. 模拟机器人行走
这是一道 中等难度 的题
https://leetcode.cn/problems/walking-robot-simulation/description/
题目
机器人在一个无限大小的 XY 网格平面上行走,从点 (0, 0) 处开始出发,面向北方。该机器人可以接收以下三种类型的命令 commands :
- -2 :向左转 90 度
- -1 :向右转 90 度
- 1 <= x <= 9 :向前移动 x 个单位长度
在网格上有一些格子被视为障碍物 obstacles 。第 i 个障碍物位于网格点 obstacles[i] = (xi, yi) 。
机器人无法走到障碍物上,它将会停留在障碍物的前一个网格方块上,但仍然可以继续尝试进行该路线的其余部分。
返回从原点到机器人所有经过的路径点(坐标为整数)的最大欧式距离的平方。(即,如果距离为 5 ,则返回 25 )
注意:
- 北表示 +Y 方向。
- 东表示 +X 方向。
- 南表示 -Y 方向。
- 西表示 -X 方向。
示例 1:
输入:commands = [4,-1,3], obstacles = []
输出:25
解释: 机器人开始位于 (0, 0): 1. 向北移动 4 个单位,到达 (0, 4) 2. 右转 3. 向东移动 3 个单位,到达 (3, 4) 距离原点最远的是 (3, 4) ,距离为 32 + 42 = 25
示例 2:
输入:commands = [4,-1,4,-2,4], obstacles = [[2,4]]
输出:65
解释:机器人开始位于 (0, 0):
1. 向北移动 4 个单位,到达 (0, 4)
2. 右转
3. 向东移动 1 个单位,然后被位于 (2, 4) 的障碍物阻挡,机器人停在 (1, 4)
4. 左转
5. 向北走 4 个单位,到达 (1, 8) 距离原点最远的是 (1, 8) ,距离为 12 + 82 = 65
提示:
- 1<=commands.length<=1041 <= commands.length <= 10^41<=commands.length<=104
- commands[i] is one of the values in the list [-2,-1,1,2,3,4,5,6,7,8,9].
- 0<=obstacles.length<=1040 <= obstacles.length <= 10^40<=obstacles.length<=104
- −3∗104<=xi,yi<=3∗104-3 * 104 <= xi, yi <= 3 * 10^4−3∗104<=xi,yi<=3∗104
- 答案保证小于 2312^{31}231
题解思路
这道题理解起来其实很简单,就是求机器人走过的点位当中离原点(0,0)(0,0)(0,0)最远的点(x,y)(x,y)(x,y),并计算其欧式距离的平方。
具体实现逻辑为: 循环遍历命令行数组 commands:
- 如果遇到
-2和-1就切换机器人方向。 - 如果遇到
1 <= x(前进步数) <= 9按照当前方向一步一步前进。- 如果将要前进到的位置
(x, y)在给定的障碍物obstacles数组中,就停下不能走了,也就是直接退出然后执行下一个命令command。 - 否则每走一步,就计算一下
ans = Math.max(ans, x2 + y2)。
- 如果将要前进到的位置
示例2 图示:
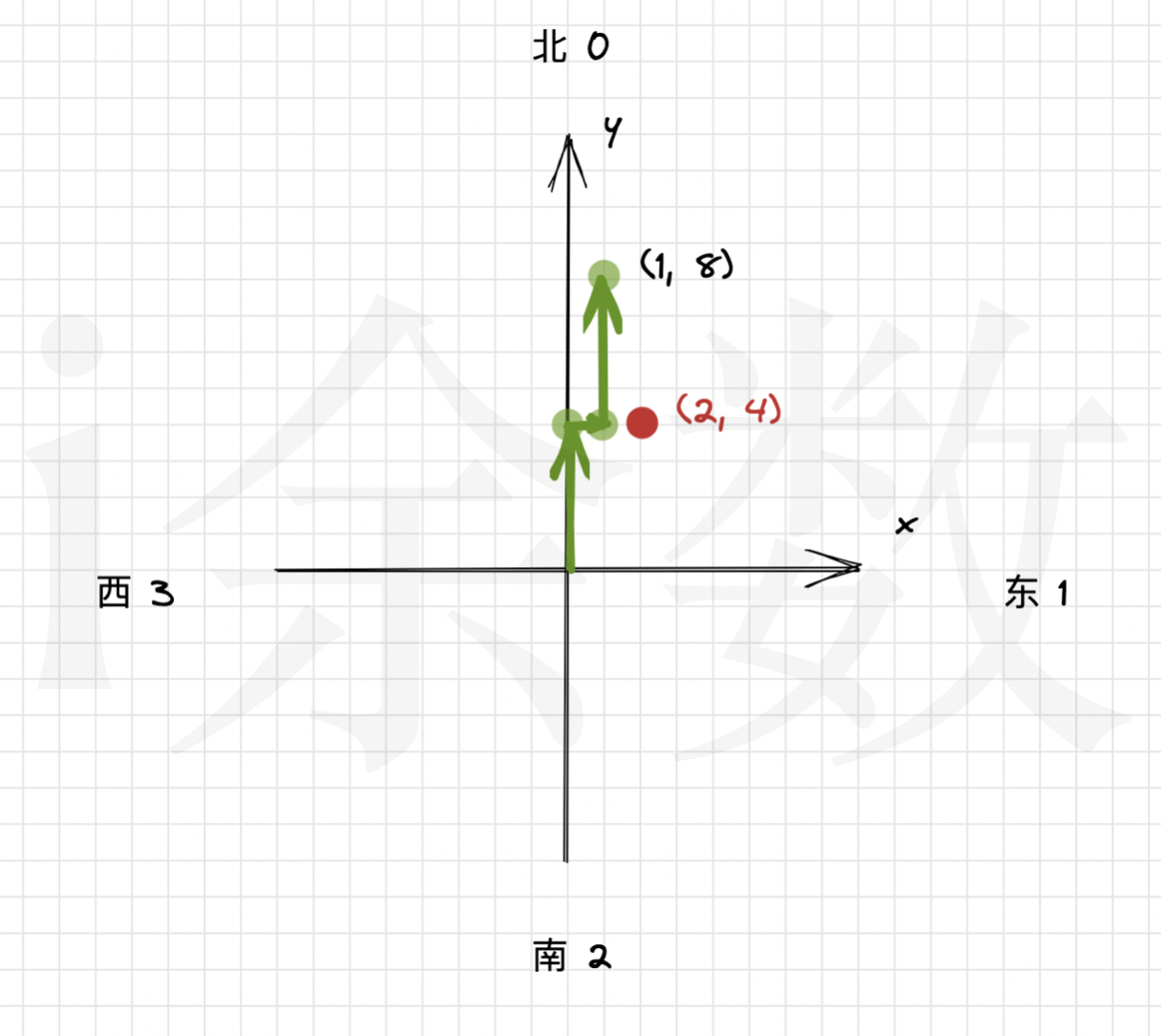
代码实现的难点在于方向的切换,这一类题目我们统一采用 方向数组 来处理。
我们定义当前方向为dir,可取值为 {0,1,2,3} ;分别代表 {北,东,南,西} 。见上图。
那么当机器人遇到改变方向的命令时,我们直接修改dir的值即可:
右转:加一,dir = (dir + 1) % 4。
左转:减一,dir = (dir - 1 + 4) % 4。因为dir - 1可能为负,所以先加4。
然后再分别在x 和 y 两个方向上定义两个方向数组,以Java为例:
int[] dx = {0, 1, 0, -1};
int[] dy = {1, 0, -1, 0};
- 方向为北(0)时:每次前进 x 不变,y 加一。
- 方向为东(1)时:每次前进 x 加一,y 不变。
- 方向为南(2)时:每次前进 x 不变,y 减一。
- 方向为西(3)时:每次前进 x 减一,y 不变。
当遇到行走命令时,每前进一步,其位置变换就应该是(x + dx[dir], y + dy[dir])。
另外需要注意的一点是,如果每次判断(x,y)(x, y)(x,y)是不是障碍物点都从 obstaclesobstaclesobstacles 数组找一次的话,那么光查找障碍点的时间复杂度就已经是 O(mn)O(mn)O(mn)了, 其中 mmm 为机器人行走的步数,nnn 为障碍物的个数。我们可以提前以O(n)O(n)O(n)的时间复杂度,将障碍物点初始化到一个哈希表当中,然后我们就可以O(1)O(1)O(1)的时间复杂度来判断一个点是不是障碍物了,具体实现见代码。
代码实现
Java代码实现
class Solution {private Set<Integer> obstacleSet = new HashSet<>();private int factor = 100000;public int robotSim(int[] commands, int[][] obstacles) {genObstacleSet(obstacles);// 当前方向,北:0, 东:1,南:2, 西:3int dir = 0;// 方向数组int[] dx = {0, 1, 0, -1};int[] dy = {1, 0, -1, 0};// 机器人位置int x = 0, y = 0; int ans = 0;for(int command : commands){if(command == -2){dir = (dir + 3) % 4;continue;}if(command == -1){dir = (dir + 1) % 4;continue;}for(int i = 0; i < command; i++){// 如果遇到障碍物,停止在当前位置if(isObstacle(x + dx[dir], y + dy[dir])){break;}x += dx[dir];y += dy[dir];ans = Math.max(ans, x * x + y * y);}}return ans;}// 判断是否是障碍物private boolean isObstacle(int x, int y){return obstacleSet.contains(factor * x + y);}private void genObstacleSet(int[][] obstacles){for(int[] obstacle : obstacles){obstacleSet.add(factor * obstacle[0] + obstacle[1]);}}
}
Go代码实现
func robotSim(commands []int, obstacles [][]int) int {// 初始化障碍点位obstacleMap := make(map[[2]int]bool)for _, obstacle := range obstacles {obstacleMap[[2]int{obstacle[0], obstacle[1]}] = true}// 当前方向dir := 0// 方向数组dx, dy := []int{0, 1, 0, -1}, []int{1, 0, -1, 0}// 当前位置x, y := 0, 0// 答案ans := 0for _, command := range commands {if command == -2 {dir = (dir + 3) % 4continue}if command == -1 {dir = (dir + 1) % 4continue}for i := 0; i < command; i++ {// 遇到障碍物if _, ok := obstacleMap[[2]int{x + dx[dir], y + dy[dir]}]; ok {break;}x += dx[dir]y += dy[dir]ans = max(ans, x * x + y * y)}}return ans}func max(a int, b int) int {if a > b {return a}return b
}
复杂度分析
-
时间复杂度:O(m+n+k)O(m + n + k)O(m+n+k), 其中 mmm 为机器人行走的步数,nnn 为障碍物的个数,kkk为转换方向的次数。
-
空间复杂度:O(n)O(n)O(n), nnn 为障碍物的个数。
