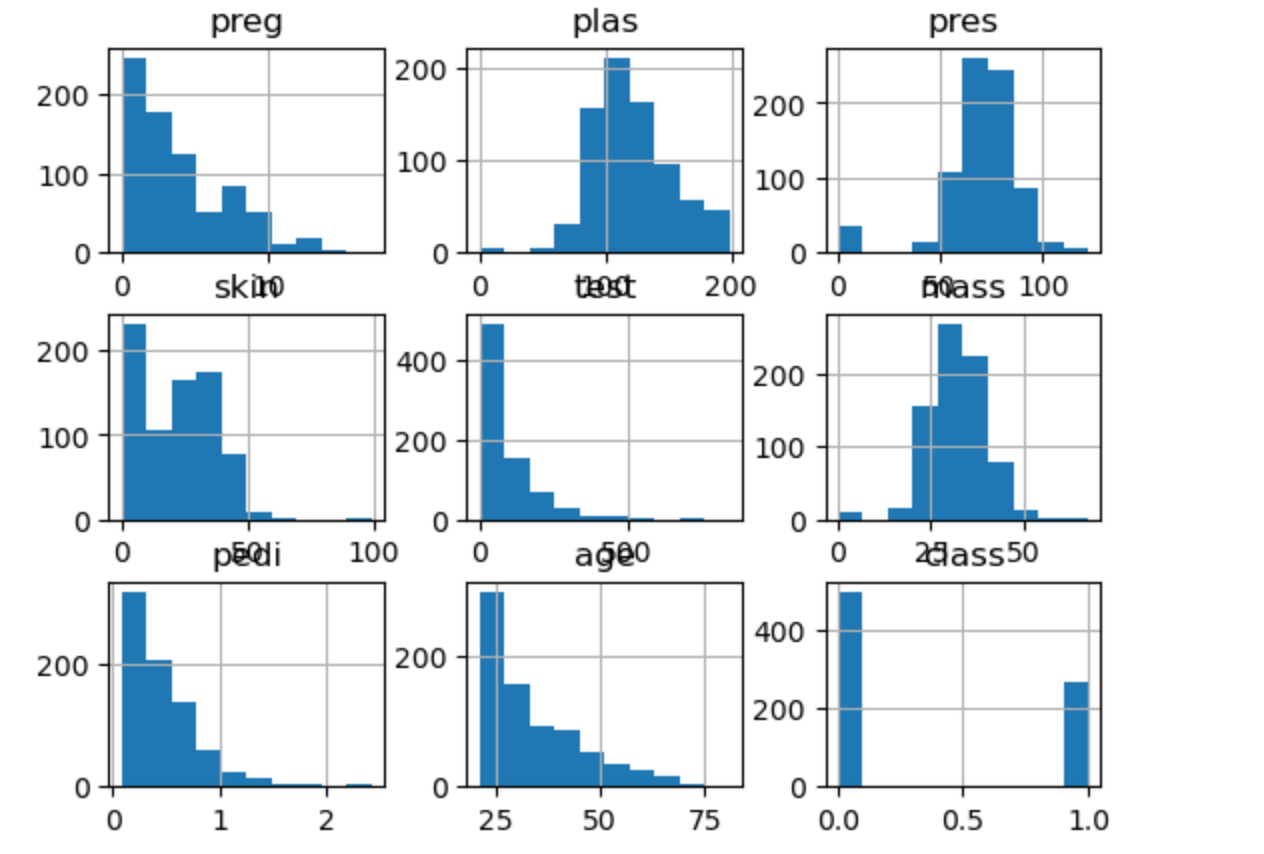
【机器学习】数据理解：数据导入、数据审查与数据可视化

一、机器学习数据导入

1、 Pandas：机器学习数据导入的最佳选择

Pandas DataFrame的数据结构优势

Pandas之所以成为机器学习数据导入的首选，核心在于其DataFrame数据结构。DataFrame不仅是一个二维表格，更是一个为数据科学量身定制的数据容器：

• 列式存储：每列可以是不同数据类型，完美适配机器学习特征的多样性
• 索引系统：内置行列索引，支持快速数据定位和切片
• 内存优化：自动类型推断和内存管理，避免不必要的内存浪费

 

2、与其他方法的差异

让我们通过实际代码来对比三种方法的差异：

方法1：Python标准库 - 手动处理每个细节

from csv import reader
import numpy as npfilename = 'pima_data.csv'
with open(filename, 'rt') as raw_data:readers = reader(raw_data, delimiter=',')x = list(readers)data = np.array(x).astype('float')  # 手动类型转换print(data.shape)

方法2：NumPy - 适合纯数值数据

from numpy import loadtxtfilename = 'pima_data.csv'
with open(filename, 'rt') as raw_data:data = loadtxt(raw_data, delimiter=',')print(data.shape)

方法3：Pandas - 一行代码完成复杂任务

from pandas import read_csvfilename = 'pima_data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(filename, names=names)
print(data.shape)

 
核心差异分析：

Pandas的优势不仅在于语法简洁，更重要的是它在背后自动处理了复杂逻辑：

1. 自动类型推断：无需手动指定数据类型，智能识别数字、文本、日期
2. 缺失值处理：自动将空值转换为NaN，统一处理逻辑
3. 列名管理：支持自定义列名，便于后续数据操作
4. 内存优化：大文件时采用懒加载策略，避免内存溢出

而标准库和NumPy都需要手动处理这些细节，导致代码复杂度呈指数级增长。

 
选择推荐

场景	推荐方案	原因
机器学习项目	Pandas	生态完整，与scikit-learn无缝集成
大规模数值计算	NumPy + Pandas	结合NumPy的计算性能和Pandas的易用性
简单数据处理	标准库	无外部依赖，适合轻量级场景

 

二、机器学习数据理解的系统化方法论

数据理解的本质不是简单的数据浏览，而是通过系统化的观察和分析，发现数据中隐藏的模式、问题和机会，从而指导后续的特征工程和算法选择。

一个经典的失败案例：某团队花费3个月训练复杂的深度学习模型，准确率始终无法提升。最后发现问题出在数据上—目标变量分布极不均衡（99%为负例），而他们从未做过类别分布分析。

 

1、数据审查方法论：六维数据画像技术

一个完整的数据画像需要从六个维度进行审查：

维度1：数据结构审查

from pandas import read_csvfilename = 'pima_data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(filename, names=names)# 查看数据规模和结构
print(data.shape)
print(data.dtypes)

关键问题：数据规模是否足够？特征类型是否合理？

 

维度2：数据质量检查

# 查看前10行，发现数据模式
print(data.head(10))# 描述性统计，发现异常值
print(data.describe())

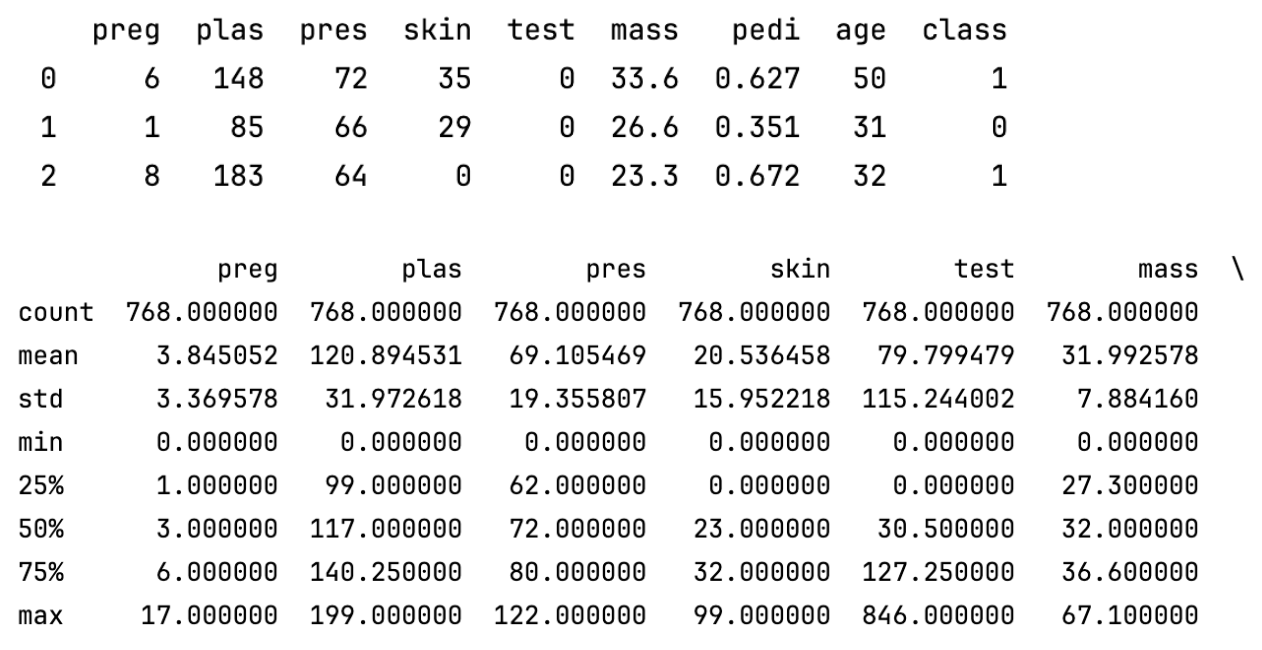
说明了数据集中各数值型特征的分布情况，包括均值、极值、分布范围等。通过这些统计量，可以初步发现数据中的异常值（比如最大值或最小值远离均值，或者四分位数间距很大等）。

关键问题：是否存在缺失值？数值范围是否合理？

 

维度3：目标变量分析

# 类别分布分析
print(data.groupby('class').size())

• 分析数据集中class这一列的类别分布情况，即每个类别有多少条数据。
• 常用于分类问题的数据探索阶段，帮助了解各类别样本是否均衡。

关键问题：类别是否均衡？是否需要重采样？

 

维度4：特征关联分析

from pandas import set_optionset_option('display.width', 100)
set_option('display.precision', 2)
print(data.corr(method='pearson'))

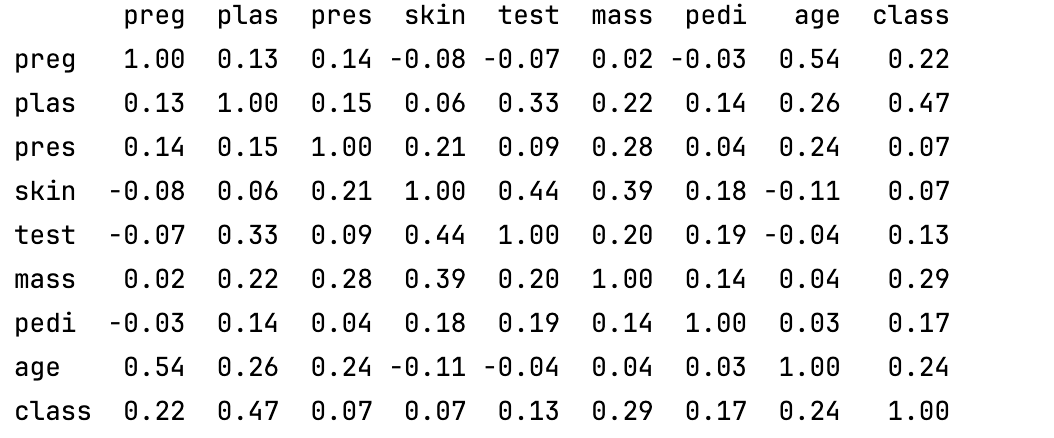
• 计算了皮尔逊相关系数矩阵。皮尔逊相关系数反映了两个变量之间的线性相关程度，取值范围为 [-1, 1]，1 表示完全正相关，-1 表示完全负相关，0 表示无线性相关。
• 即数据集中各数值型特征之间的相关性矩阵，方便你分析变量之间的关系。

关键问题：哪些特征与目标变量强相关？是否存在多重（ing）共线性？

 

维度5：数据分布特征

# 计算偏态系数
print(data.skew())

偏态系数衡量的是数据分布的对称性。
偏态系数 = 0，表示分布完全对称（如正态分布）。
偏态系数 >0，表示分布右偏（长尾在右边，数据集中在左边）。
偏态系数 < 0，表示分布左偏（长尾在左边，数据集中在右边）。
 
通过查看偏态系数，可以判断数据是否偏离正态分布。偏态较大的特征，可能需要做对数变换、Box-Cox变换等预处理，以便更好地建模。

关键问题：数据分布是否符合算法假设？是否需要变换？

 

维度6：数据完整性

# 检查缺失值
print(data.isnull().sum())

 

这六个维度的检查顺序遵循了从宏观到微观，从结构到内容的认知规律：

• 结构审查建立整体的数据认知
• 质量检查发现数据可靠性问题
• 目标分析明确建模难度和策略
• 关联分析揭示特征工程方向
• 分布分析指导算法选择
• 完整性检查确定数据清洗优先级

 

2、从数据观察到算法选择的逻辑链条

1、数据特征→算法匹配

通过系统化的数据理解，我们可以建立数据特征到算法选择的映射关系：

数据特征	算法选择	原因
数值型+线性关系	线性回归、岭回归	符合线性假设，计算效率高
高维稀疏数据	逻辑回归、SVM	处理高维特征能力强
类别不均衡	随机森林+重采样	对不均衡数据鲁棒性好
非线性关系复杂	梯度提升树、神经网络	强大的非线性拟合能力

 

2、决策示例

假设通过数据理解发现：

目标变量类别比例为7:3（轻度不均衡）、特征间存在中等程度相关性（0.3-0.6）、部分特征呈现右偏分布。

决策逻辑：

1. 类别不均衡程度中等 → 可以使用类别权重平衡，无需重采样
2. 特征相关性适中 → 可以保留所有特征，无需降维
3. 数据右偏 → 建议使用基于树的算法（对分布不敏感）

推荐算法：随机森林 + 类别权重调整

 

三、数据可视化驱动的机器学习决策

可视化的核心价值：它能够揭示统计数字背后的数据结构、异常模式和潜在关系，让我们在建模之前就能洞察数据的本质特征。

一个典型的例子：某数据科学家通过describe()发现某特征均值为50，看似正常。但通过箱线图可视化后发现，数据呈现双峰分布，实际上是两个不同群体的混合，这直接影响了后续的特征工程策略。

1、五维可视化分析

下面将从分布、异常、连续性、关联、交互五个维度进行系统化分析

维度1：直方图：分布形态分析 - "数据长什么样？

from pandas import read_csv
import matplotlib.pyplot as pltfilename = 'pima_data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(filename, names=names)# 直方图 - 揭示频率分布
data.hist()
plt.show()

代码为数据集中的每个数值型特征绘制直方图，直观展示其取值分布和频率，帮助你了解数据的整体分布特征。

核心洞察：直方图能够识别数据的分布类型（正态、偏态、双峰），这直接影响算法选择。

 

维度2：箱线图：分布细节分析 - “异常值在哪里？”

# 箱线图 - 识别异常值和四分位数
data.plot(kind='box', subplots=True, layout=(3,3), sharex=False)
plt.show()

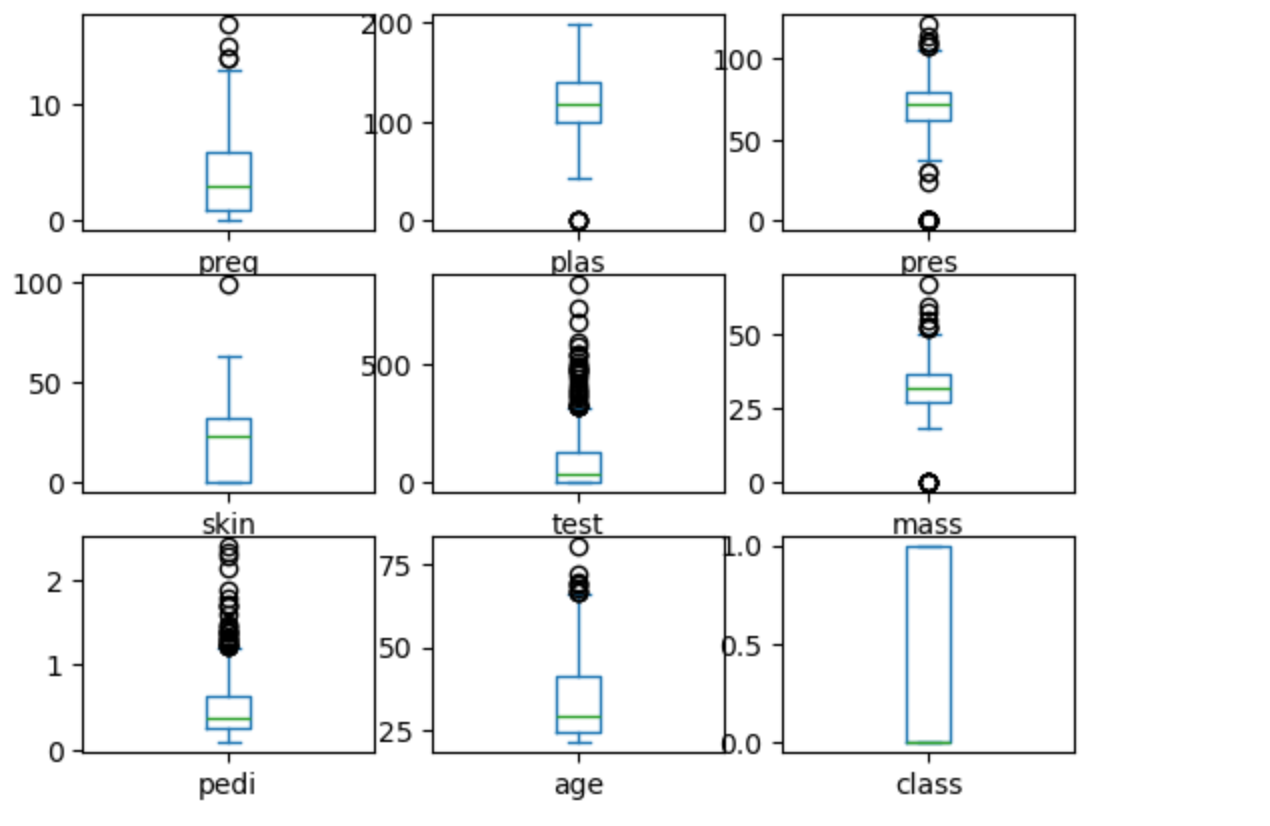
箱线图（Boxplot）是一种常用的统计图表，用于展示数据的分布特征、中心位置、离散程度以及异常值。
 
箱线图的结构

• 箱体（Box）：表示数据的中间50%（从第1四分位数Q1到第3四分位数Q3）。
• 中位线（Median）：箱体中间的绿线，表示数据的中位数（第2四分位数Q2）。
• “胡须”（Whiskers）：从箱体延伸出去的线，通常延伸到1.5倍四分位距（IQR）以内的数据。（IQR=Q3-Q1，四分位距 ing）。
• 异常值（Outliers）：超出“胡须”范围的点，单独以小圆点等方式标出。

具体分析

一、preg, plas, pres, skin, test, mass, pedi, age 字段数据

1. 这些特征的箱线图都显示了不同程度的异常值（上方或下方的圆点），说明这些特征中有一些数据点远离主流分布，可能是极端值或录入错误。
2. 箱体高度：箱体越高，说明该特征的中间50%数据分布越分散；越矮则越集中。 中位线位置：如果中位线偏向箱体上方或下方，说明数据分布有偏态。
    

二、class 字段数据
这个特征的箱线图显示为0和1的分布（因为是分类变量），没有异常值，箱体覆盖了0和1两个取值。
 
三、结论

1. 异常值：如test、skin、pedi等特征有较多异常值（上方或下方的圆点）。
2. 分布偏态：如preg、pedi等特征的中位线偏下，说明数据右偏。
3. 数据分布：大部分特征的箱体都比较靠近下方，说明数据集中在较小的取值区间，少数点取值很大。

通过这些箱线图，你可以快速发现哪些特征有异常值、分布是否偏态、数据是否集中等，为后续的数据清洗和建模提供依据。

 

维度3：密度图：连续性分析 - “数据如何变化？”

# 密度图 - 显示连续分布特征
data.plot(kind='density', subplots=True, layout=(3,3), sharex=False)
plt.show()

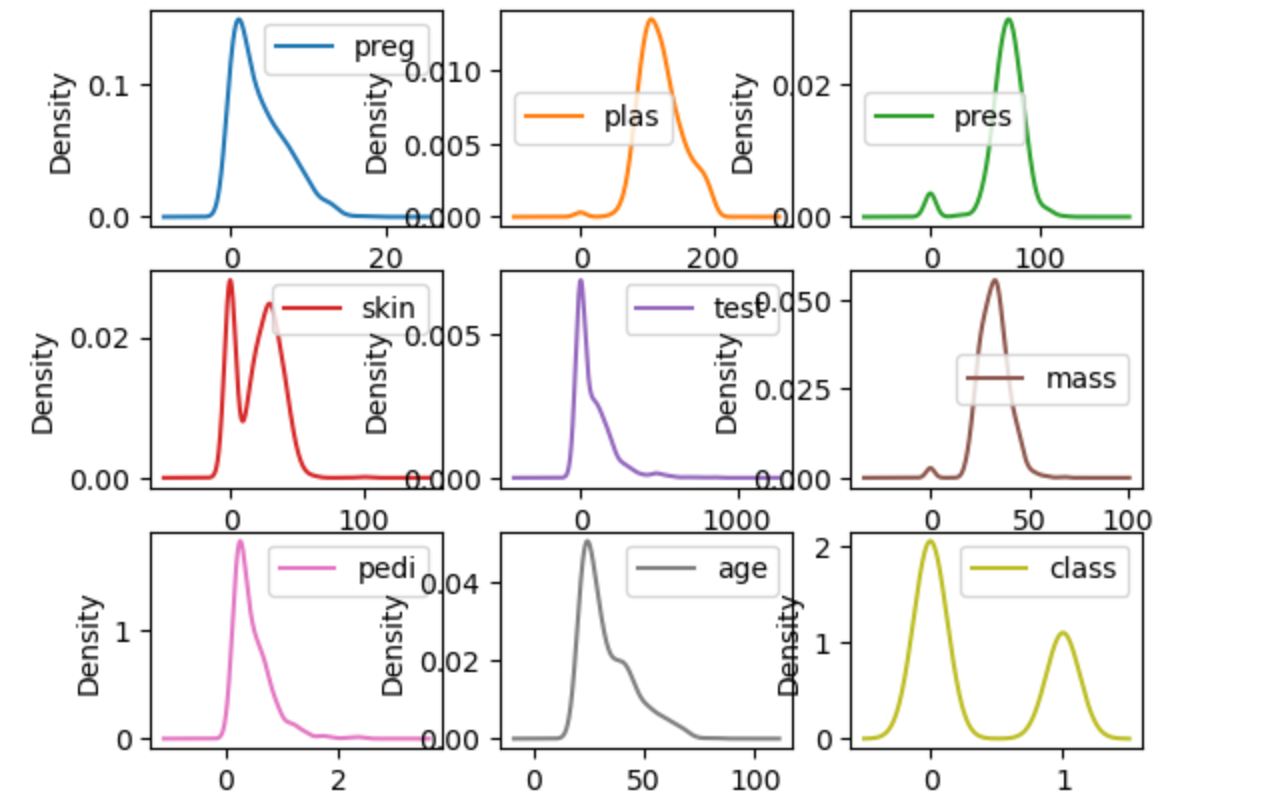
密度图能说明什么？

1. 数据的分布形态：可以直观地看到数据是单峰（一个高峰）、多峰（多个高峰）、偏态（左偏/右偏）还是近似正态分布。 比直方图更平滑，能更好地反映数据的真实分布趋势。
2. 数据的集中趋势和离散程度：峰值高且窄，说明数据集中在某个区间。 峰值低且宽，说明数据分布较分散。
3. 是否有异常分布或多重分布：如果密度图有多个峰，说明数据可能由多个不同的子群体组成（多模态分布）。 可以辅助发现异常值（极端的孤立小峰）。
4. 数据的偏态情况：峰值偏左，右侧尾巴长，说明右偏（正偏态）。 峰值偏右，左侧尾巴长，说明左偏（负偏态）。

核心洞察：密度图能够发现数据的平滑分布模式，识别潜在的数据生成机制。

 

维度4：热力图：关联强度分析 - “特征间如何影响？”

import numpy as np# 相关性热力图 - 显示特征间关联强度
correlations = data.corr()
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(correlations, vmin=-1, vmax=1)
fig.colorbar(cax)
ticks = np.arange(0, 9, 1)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_xticklabels(names)
ax.set_yticklabels(names)
plt.show()

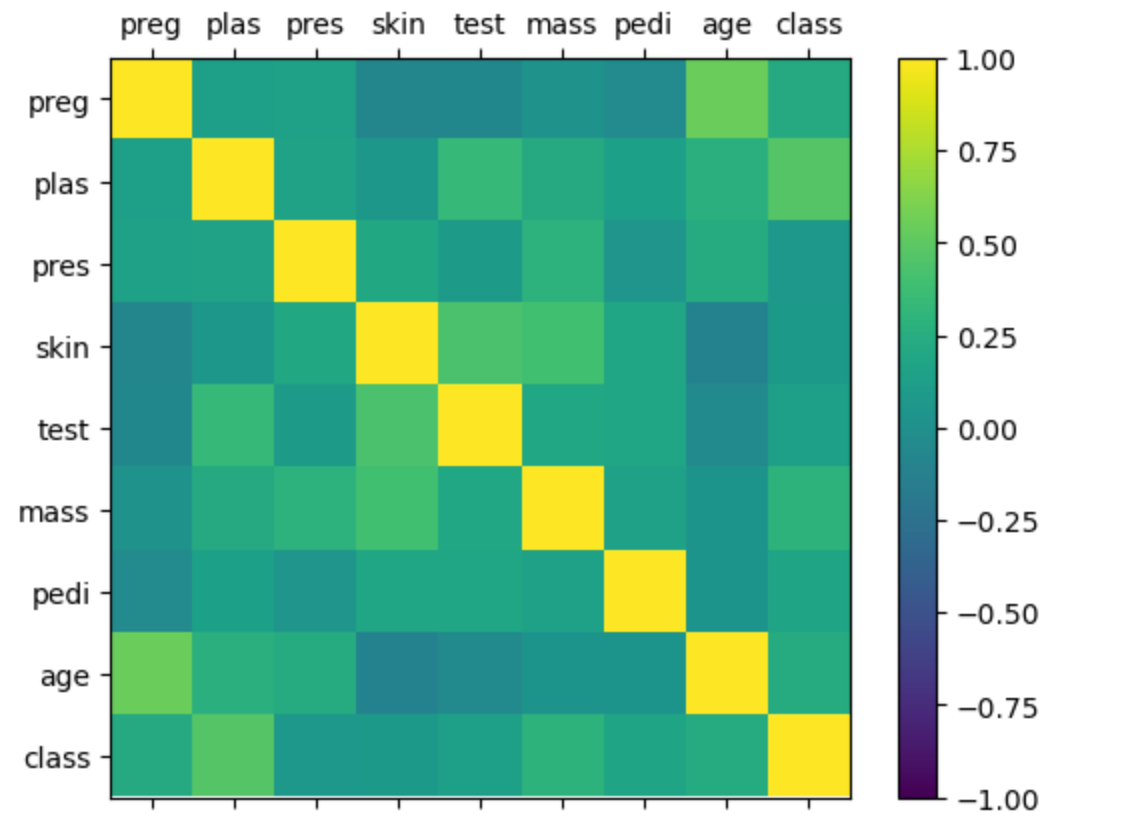
热力图是一种用颜色深浅来表示数值大小的可视化方式。在相关性热力图中，每个格子代表两个特征之间的相关系数（correlation coefficient），颜色越接近黄色，相关性越强（正相关）；颜色越接近深蓝色，相关性越弱或为负相关。

热力图的作用

• 发现强相关特征：如果两个特征高度相关，可能存在冗余，可以考虑去除其中一个，避免多重共线性。
• 发现无关特征：相关系数接近0的特征对彼此影响小，适合独立建模。
• 辅助特征工程：根据相关性调整特征选择、降维等策略。

图中的对角线都是黄色（相关系数为1）。其他格子的颜色大多为绿色或青色，说明大部分特征之间的线性相关性不强。如果有某两个特征之间的格子颜色明显偏黄或偏蓝，说明它们之间有较强的正相关或负相关关系。

 

维度5：关系模式分析 - “特征间如何交互？”

from pandas.plotting import scatter_matrix# 散点图矩阵 - 显示特征间非线性关系
scatter_matrix(data)
plt.show()

1. 什么是散点矩阵图？
   散点矩阵图会将数据集中的每一对数值型特征都画成一个散点图，排列成一个矩阵。 对角线上的图通常是每个特征的直方图（显示该特征的分布）。 非对角线上的每个小图，表示两个特征之间的散点分布关系。
2. 散点矩阵图能看出什么？
   • 特征之间的关系：可以直观地看到任意两列特征之间的关系（线性、非线性、无关等）。
     a. 如果两个特征之间的点分布成一条直线，说明它们高度线性相关。
     b. 如果点分布成某种曲线，说明它们有非线性关系。
     c. 如果点分布很分散，没有明显形状，说明它们之间没有明显关系。
   • 异常值: 可以发现某些特征组合下的极端点（离群点）。
   • 分布特征：对角线上的直方图显示每个特征的分布形态（如正态分布、偏态、多峰等）。
   • 多重共线性：如果某两列的散点图呈现出很强的线性关系，说明这两个特征可能存在多重共线性。

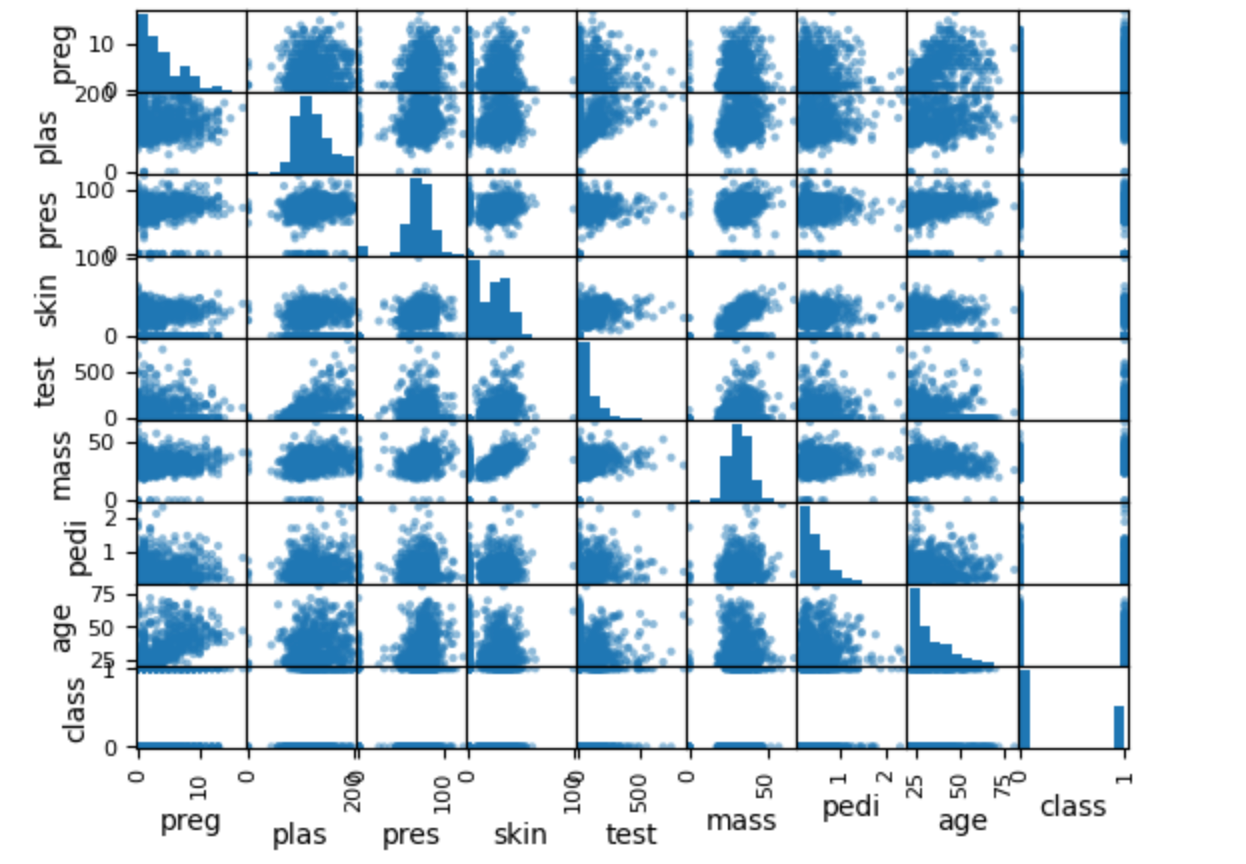
散点图矩阵能够全面、直观地展示数据集中各特征之间的两两关系和各自分布。
帮助你发现特征间的相关性、异常值、分布形态等，为后续的数据预处理和特征工程提供依据。

 

2、"观察-提问-决策"闭环系统

可视化分析的核心不是看图，而是建立从观察到决策的逻辑链条：

第一步：结构化观察

• 分布形态：是否符合正态分布？
• 异常值：异常值比例和位置？
• 关联性：哪些特征强相关？

第二步：关键问题提炼

• 数据质量：异常值是噪声还是有价值的信号？
• 特征工程：是否需要变换或组合特征？
• 算法选择：数据特征适合哪类算法？

第三步：决策规则制定

观察结果	提问	决策行动
数据严重偏态	是否需要变换？	应用对数变换或Box-Cox变换
存在强相关特征	是否存在冗余？	考虑降维或特征选择
发现异常值聚集	是否为特殊群体？	分层建模或异常检测
非线性关系明显	线性模型是否适用？	选择基于树或核方法的算法

 

1、示例说明

假设通过五维可视化发现：

• 直方图显示：目标变量呈现双峰分布；
• 箱线图显示：某特征存在大量异常值；
• 相关性图显示：两个特征高度相关（r>0.8）；
• 散点图显示：特征与目标存在明显非线性关系。

决策逻辑：

1. 双峰分布 → 可能存在隐含的数据子群 → 考虑聚类或分层建模
2. 大量异常值 → 需要异常值处理策略 → 使用鲁棒性强的算法
3. 高度相关特征 → 存在多重共线性 → 进行特征选择或正则化
4. 非线性关系 → 线性模型不适用 → 选择随机森林或XGBoost

最终决策：使用随机森林算法 + 特征选择 + 异常值处理的组合策略

 

2、可视化驱动的工作流