当前位置：首页 > news >正文

《剑指offer》——从尾到头打印链表

news 2025/9/17 11:07:12

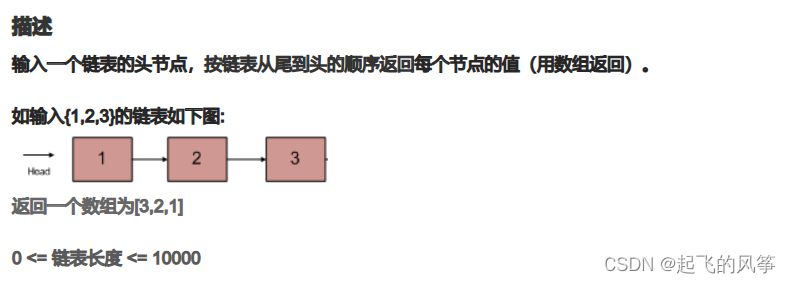
首先，拿到题之后，我们还是先从题目入手，只有掌握题干的意思，才能进行接下来的解题操作。

示例1

输入 : {1,2,3}
返回值：[3,2,1]

示例2

输入：{67,0,24,58}

返回值：[58,24,0,67]

解题方法

a）直接遍历法

b）递归思想

c）栈思想

题目解析：

首先，拿到这个题，读过题之后我们会发现题意很简单，就是让我们针对链表中的元素，把它从尾到头输出即可。接下来，我提供给大家三种解题思路。

a）直接遍历法

💨思路：

我们先开辟一个数组，紧接着我们可以直接对这个链表进行从头节点开始的遍历操作。
记录下这个链表中的每个节点的值，把相应的值放入我们建立的数组之中。
最后遍历完毕在反转一下整个数组，返回即可。

代码如下：

class Solution {
public:vector<int> printListFromTailToHead(ListNode* head) {vector<int>arr;  //开辟的数组用来存放链表中的值while(head){arr.push_back(head->val); //进行遍历操作，把元素插入数组head=head->next;}reverse(arr.begin(),arr.end());//最后反转数组即可return arr;}
};

性能分析：

时间复杂度：因为需要直接遍历长度为n的链表的所有的结点，所以时间复杂度为O(n)
空间复杂度：因为我们开辟了一个链表大小数组的用来存放链表结点中的值，因此空间复杂度为O(n)

b）递归思想

首先解答一下什么是递归：

首先，绝大多数问题都可以划分成更小的问题，通过求解这些小问题，将结果合并在一起得到原本问题的答案，其实递归的本质就是函数调用而已。因此，接下来的关键就是通过题意查看是否可以拆分为一个个的子问题。

💨思路：

首先，我们应该明白一点知识点，那就是我们对于链表来说，我们是不能直接通过遍历链表就得到题目所要求的从尾向头输出链表中的结点值。
所以我们可以对遍历的结点进行一个递归，我们先递归到这个链表的最后面，然后不断向前收集查看结点的权值。

代码如下：

//递归思想
void recursion(ListNode* head,vector<int>&arr)
{if(head != NULL){recursion(head->next,arr); //如果当前指针不为空，则一直往后进行递归操作arr.push_back(head->val);  //遇到尾节点后开始返回，每次返回依次添加一个值进入输出数组}
}class Solution {
public:vector<int> printListFromTailToHead(ListNode* head) {vector<int>arr;  //还是跟之前一样，开辟一个数组用来存放链表中结点的值recursion(head,arr); //递归调用去进行查看return arr;}
};

性能分析：

时间复杂度：因为需要直接遍历长度为n的链表的所有的结点，所以时间复杂度为O(n)
空间复杂度：因为我们开辟了一个链表大小的组用来存放链表中结点的值，因此空间复杂度为O(n)

c）栈思想

首先认识一下栈

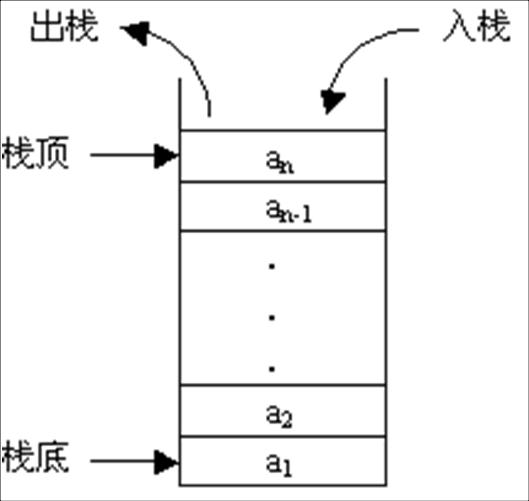
首先，站的基本思想就是先进后出，如果对栈不了解的，可以参考这篇文章栈的实现，它的基本思想满足本题中对链表进行从尾到头输出的条件。

💨思路：

我们可以从头结点开始顺序遍历整个链表，遍历的过程中将链表结点的值依次push到栈中
遍历完之后，再依次弹出栈中的元素，加入到数组中
最后返回数组，即可实现本题所要求的逆序输出

代码如下：

//栈思想class Solution {
public:vector<int> printListFromTailToHead(ListNode* head) {vector<int>arr;  //还是跟之前一样，开辟一个数组用来存放链表中结点的值stack<int> str;  //定义的栈while(head != NULL){str.push(head->val); //首先遍历链表，把其中结点的权值全部压入栈中head=head->next;}while(!str.empty()){//因为要求用数组返回把栈中的所有元素全部尾插到数组中arr.push_back(str.top());//弹出栈中的元素，即表示逆序输出的结果str.pop();                  }//最后返回数组的内容return arr;}
};

性能分析：