神经网络激活函数
神经网络激活函数
- 神经网络激活函数的定义
- 为什么神经网络要用激活函数
- 神经网络激活函数的求导
- Sigmoid激活函数
- Tanh激活函数
- Softmax激活函数
神经网络激活函数的定义
所谓激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。
激活函数(Activation functions)对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。如图:
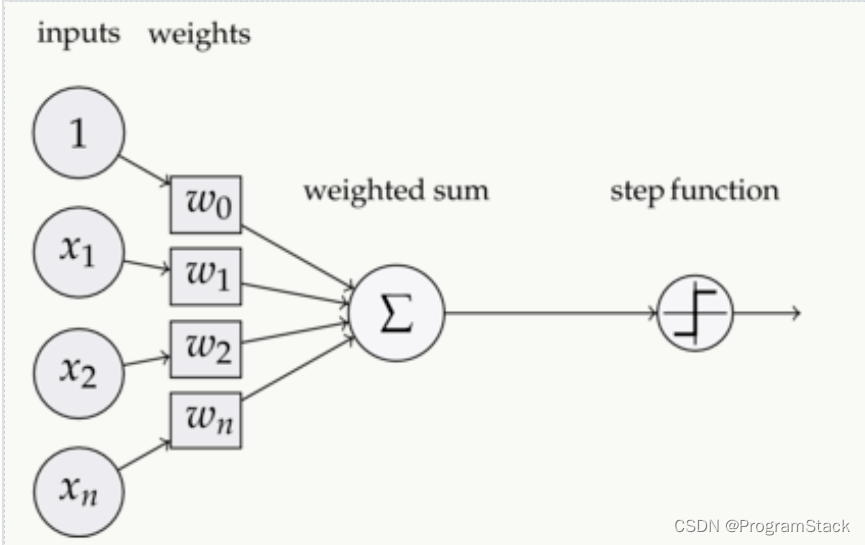
在神经元中,输入的 inputs 通过加权,求和后,还被作用了一个函数,这个函数就是激活函数。引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。
为什么神经网络要用激活函数
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。
如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
神经网络激活函数的求导
对神经网络激活函数求导有一个特性,它的导函数始终都可以用原式表示出来,下面列举常用神经网络激活函数:
Sigmoid激活函数
表达式为:σ(x)=11+e−x\sigma (x) = \frac{1}{1+e^{-x}}σ(x)=1+e−x1
函数图像如下:
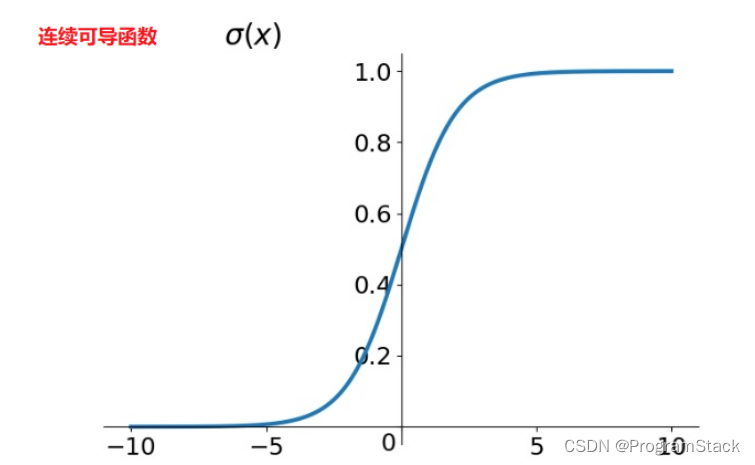
其导函数:σ′(x)=∂∂x11+e−x=11+e−x∗(1−11+e−x)=σ(x)∗(1−σ(x))\sigma'(x) = \frac{\partial}{\partial x}\frac{1}{1+e^{-x}} = \frac{1}{1+e^{-x}}*(1-\frac{1}{1+e^{-x}})=\sigma(x)*(1-\sigma(x))σ′(x)=∂x∂1+e−x1=1+e−x1∗(1−1+e−x1)=σ(x)∗(1−σ(x))
Tanh激活函数
表达式为:tanh(x)=ex−e−xex+e−x=21+e−2x−1tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{2}{1+e^{-2x}}-1tanh(x)=ex+e−xex−e−x=1+e−2x2−1
而我们的Sigma激活函数表达式为σ(x)=11+e−x\sigma (x) = \frac{1}{1+e^{-x}}σ(x)=1+e−x1,所以Tanh激活函数可以用Sigma激活函数表示,即tanh(x)=2σ(2x)−1tanh(x) = 2\sigma(2x)-1tanh(x)=2σ(2x)−1
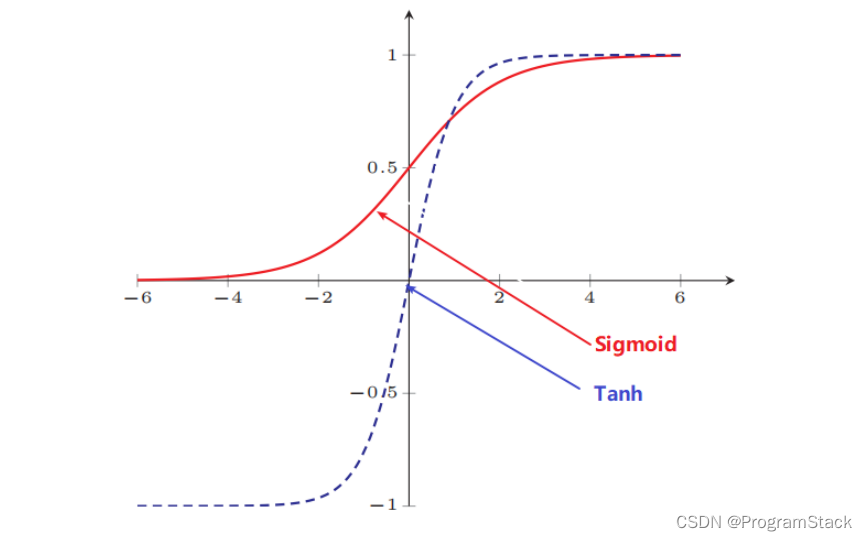
Tanh 函数可以看作是放大并平移的 Sigmoid 函数,但因为是零中心化的 (zero-centered) ,通常收敛速度快于 Sigmoid 函数,下图是二者的对比:
其导函数:tanh′(x)=(ex+e−x)2−(ex−e−x)2(ex+e−x)2=1−(ex−e−x)2(ex+e−x)2=1−tanh(x)2tanh'(x) = \frac{(e^x+e^{-x})^2-(e^x-e^{-x})^2}{(e^x+e^{-x})^2}= 1- \frac{(e^x-e^{-x})^2}{(e^x+e^{-x})^2}=1-tanh(x)^2tanh′(x)=(ex+e−x)2(ex+e−x)2−(ex−e−x)2=1−(ex+e−x)2(ex−e−x)2=1−tanh(x)2
Softmax激活函数
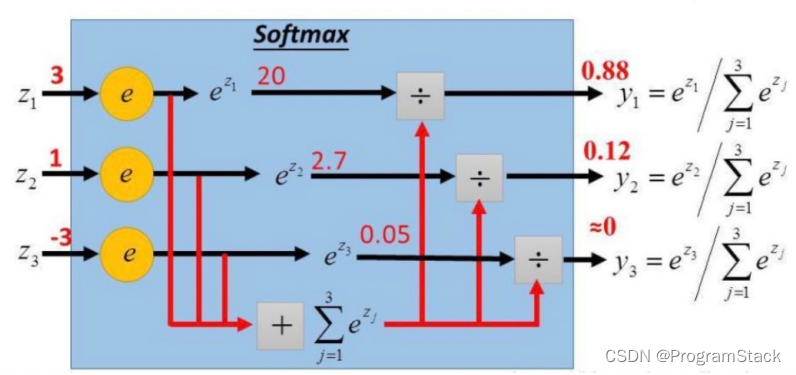
表达式:yi=softmax(zi)=ezi∑j=1Cezjy_i = softmax(z_i) = \frac{e^{z_i}}{\sum_{j=1}^Ce^{zj}}yi=softmax(zi)=∑j=1Cezjezi
Softmax函数将多个标量映射为一个概率分布,yiy_iyi表示第i个输出值,即属于类别iii的概率,所有类别概率加起来为1,即∑i=1Cyi=1\sum_{i = 1}^Cy_i = 1∑i=1Cyi=1,其中z=WTxz = W^Txz=WTx,表示线性方程,图中的ziz_izi表示zzz的第i个元素的值。Softmax函数用于多分类,会对应多个方程。
首先求标量形式的导数,即第i个输出对于第j个输入的偏导数
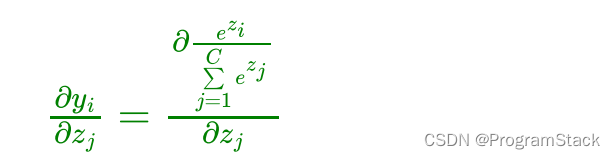
其导函数:
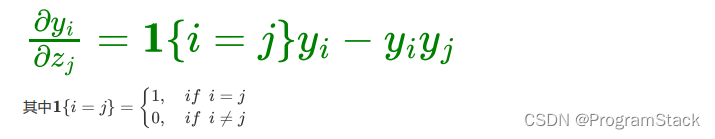
这里就不在做过多的推导了,感兴趣的小伙伴可以去翻阅书籍哦
