当前位置： 首页 > news >正文

java数据结构-栈、队列详解

news 2025/6/18 22:15:49

栈简介

请添加图片描述

  • 栈就像我们生活中堆叠的盘子一样
  • 后进先出，只能从栈顶插入或者删除元素，O(1)
  • push(x)、pop()、Top()指向栈顶元素、IsEmpty()
  • 应用：执行函数，编辑器的撤回操作，编译器使用栈可以验证代码中的括号是否匹配{[()]}

栈的实现方式

使用数组实现栈

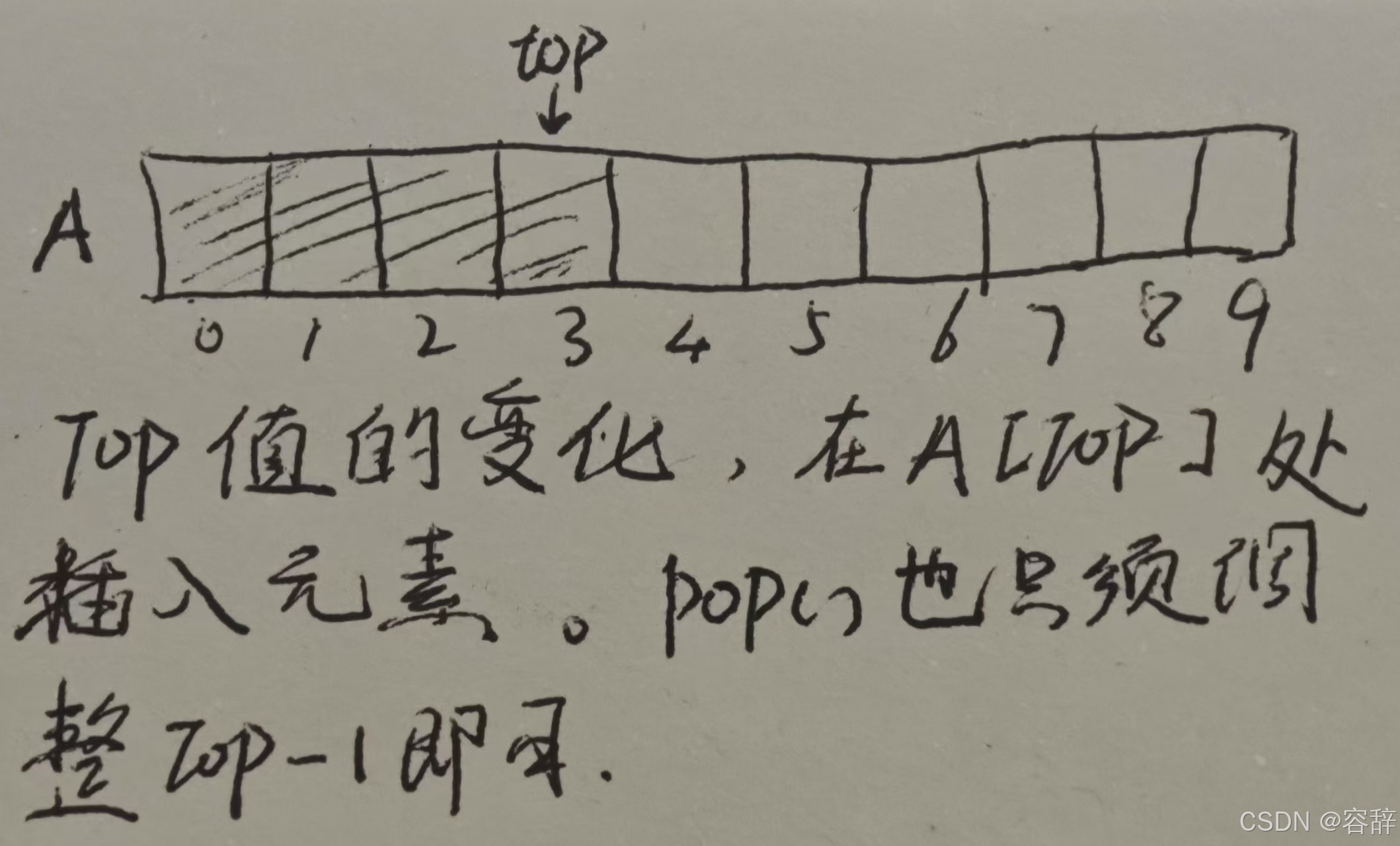
请添加图片描述

空栈top值-1，top大小不能超过数组大小，否则会栈溢出。
时间复杂度：best–O(1) 、worst–O(n)栈溢出情况需要将数组扩大，原来的数据复制到新的上面。

public class DataStruct {static final int MAX_SIZE = 10;int[] A = new int[MAX_SIZE];int top = -1;public void push(int x){if (top==MAX_SIZE-1){System.out.println("栈溢出");return;}A[++top]=x;}public void pop(){if (top==-1){System.out.println("空栈");return;}top--;}public int top(){return A[top];}public static void main(String[] args) {DataStruct ds = new DataStruct();ds.push(1);ds.print();ds.push(4);ds.print();ds.push(5);ds.print();ds.pop();ds.print();ds.push(90);ds.print();System.out.println(ds.top());}void print(){for (int i = 0; i <=top; i++) {System.out.print(A[i]);}System.out.println();}
}

使用链表实现栈

链表尾部插入或删除需要O(n)，所以我们从头部插入或删除。栈顶=表头

class Node {int data;Node next;public Node(int data){this.data = data;this.next = null;}
}
public class DataStruct {public Node push (Node head,int data){Node temp = new Node(data);temp.next = head;head = temp;return head;}public Node pop(Node head){if (head == null) return head;head = head.next;return head;}public int top(Node head){return head.data;}public static void main(String[] args) {DataStruct ds = new DataStruct();Node node = null;node = ds.push(node,1);node = ds.push(node,8);node = ds.push(node,9);node = ds.pop(node);System.out.println("栈顶："+ ds.top(node));while (node != null){System.out.println(node.data);node = node.next;}}
}

栈的使用场景

反转字符串/链表

请添加图片描述

因为栈是后入先出，所以很适合反转。java中栈是封装好的可以拿来即用（java.util.Stack）。由代码可以得到反转字符串时间/空间复杂度=O(n)，有更好的反转方法就是双指针s(n)=O(1)

import java.util.Stack;
public class DataStruct {public void reverse(char[] s){Stack<Character> stack = new Stack<>();for (int i=0;i<s.length;i++){stack.push(s[i]);}for (int i=0;i<s.length;i++){s[i]=stack.pop();}}public static void main(String[] args) {DataStruct ds = new DataStruct();char[] s = {'h','e','l','l','o'};ds.reverse(s);System.out.println(new String(s));}
}

反转链表用不了双指针，可以采用如下方法：

  • 迭代法（上篇文章）
  • 递归法（上篇文章）
  • 栈，时间/空间复杂度=O(n)
import java.util.Stack;class Node {int data;Node next;public Node(int data){this.data = data;this.next = null;}
}
public class DataStruct {public Node Reverse(Node head){if (head == null) return null;Stack<Node> s = new Stack<>();Node temp = head;while (temp!=null){s.push(temp);temp=temp.next;}temp=s.peek();//栈顶元素就是前面实现的TOP方法head=temp;s.pop();while(!s.isEmpty()){temp.next=s.pop();temp = temp.next;}temp.next=null;return head;}public static void main(String[] args) {DataStruct ds = new DataStruct();Node node = new Node(2);node.next = new Node(5);node.next.next = new Node(3);node.next.next.next = new Node(8);node = ds.Reverse(node);while (node != null){System.out.println(node.data);node = node.next;}}
}

检查括号的匹配性

匹配条件：
请添加图片描述
方案：将所有左未关闭括号放在一个list中，当出现右括号与list最后一个元素匹配，匹配上则list删除最后一个元素，直到最后列表为空，表达式也扫描完毕，则括号匹配！
这是后入先出，总从一端插入删除元素----使用栈来解决：

import java.util.Stack;
public class DataStruct {public boolean checkBalance(String exp){Stack<Character> strings = new Stack<>();for (int i=0;i<exp.length();i++){if (exp.charAt(i)=='(' || exp.charAt(i)=='[' || exp.charAt(i)=='{'){strings.push(exp.charAt(i));}if (exp.charAt(i)==')' || exp.charAt(i)==']' || exp.charAt(i)=='}'){if (strings.isEmpty()) return false;Character pop = strings.pop();if ((pop=='(' && exp.charAt(i)!=')') || (pop=='[' && exp.charAt(i)!=']') || (pop=='{' && exp.charAt(i)!='}')){return false;}}}if (!strings.isEmpty()) return false;return true;}public static void main(String[] args) {DataStruct ds = new DataStruct();String exp ="{([)}";System.out.println(ds.checkBalance(exp));String exp2 ="{()()}";System.out.println(ds.checkBalance(exp2));String exp3 ="[()}";System.out.println(ds.checkBalance(exp3));}
}

中缀/前缀/后缀

定义

请添加图片描述
从计算机角度，中缀表达式要转换为前/后缀表达式，来进行求值会更简单。括号是为了增加可读性，计算机不需要可读性，故去掉。

代码编写：后缀/前缀表达式求值

请添加图片描述

import java.util.Stack;
public class DataStruct {//后缀表达式求值:从左到右，pop2操作符pop1public int EvaluatePostfix(String exp) {Stack<Integer> stack = new Stack<>();String[] exp1 = exp.split(" ");//根据空格进行分组boolean flag = true;for(String s : exp1){try{Integer.parseInt(s);flag = true;}catch(Exception e){flag = false;}if (flag){stack.push(Integer.parseInt(s));}else {Integer pop1 = stack.pop();Integer pop2 = stack.pop();switch (s) {case "+":stack.push(pop2 + pop1);break;case "-":stack.push(pop2 - pop1);break;case "*":stack.push(pop2 * pop1);break;case "/":stack.push(pop2 / pop1);}}}return stack.peek();}//前缀表达式求值: 从右到左扫描，pop1操作符pop2public int EvaluatePrefix(String exp) {Stack<Integer> stack = new Stack<>();String[] exp1 = exp.split(" ");//根据空格进行分组//反转Stack<String> stack1 = new Stack<>();for (String s : exp1) {stack1.push(s);}for(int i=0;i<exp1.length;i++){exp1[i] = stack1.pop();}boolean flag = true;for(String s : exp1){try{Integer.parseInt(s);flag = true;}catch(Exception e){flag = false;}if (flag){stack.push(Integer.parseInt(s));}else {Integer pop1 = stack.pop();Integer pop2 = stack.pop();switch (s) {case "+":stack.push(pop1 + pop2);break;case "-":stack.push(pop1 - pop2);break;case "*":stack.push(pop1 * pop2);break;case "/":stack.push(pop1 / pop2);}}}return stack.peek();}public static void main(String[] args) {DataStruct ds = new DataStruct();String exp ="2 3 * 5 4 * + 9 -";System.out.println(ds.EvaluatePostfix(exp));}
}

中缀如何转换为后缀

操作数放在list，操作符放在栈。
请添加图片描述
遇到操作数直接放入list，遇到操作符当栈空直接放入，当遇到操作符更高的，持续放入栈中，操作符弹出栈的条件：

  • 遇见优先级低的操作符，持续弹出。但不能弹出左括号，左括号只能遇到右括号才能弹出
  • 遇见右括号
  • 字符结束

括号的情况：遇见左括号持续放入，遇见右括号持续弹出，直到弹出一个左括号结束。

import java.util.Objects;
import java.util.Stack;
public class DataStruct {public String infixToPostfix(String exp) {Stack<String> stack = new Stack<>();String[] exp1 = exp.split(" ");StringBuilder postfix = new StringBuilder();boolean flag = true;for (String s : exp1) {try{Integer.parseInt(s);flag = true;}catch(Exception e){flag = false;}if (flag){postfix.append(s);}else if (Objects.equals(s, "+") || Objects.equals(s, "-") || Objects.equals(s, "*") || Objects.equals(s, "/")){if (stack.isEmpty()){stack.push(s);continue;}String peek = stack.peek();int p1 = priority(peek);int p2 = priority(s);while(!stack.empty() && p2<=p1 && !stack.peek().equals("(")){postfix.append(stack.pop());}stack.push(s);}else if (Objects.equals(s, "(") || Objects.equals(s,")")){if (s.equals("(")){stack.push(s);continue;}while (!stack.peek().equals("(")){postfix.append(stack.pop());}stack.pop();}}while (!stack.empty()){postfix.append(stack.pop());}return postfix.toString();}//判断操作符优先级public int priority(String s){switch (s){case "+":case "-":return 1;case "*":case "/":return 2;default:return -1;}}public static void main(String[] args) {DataStruct ds = new DataStruct();String exp ="( ( 2 + 3 ) * 4 - 5 ) * 6";System.out.println(ds.infixToPostfix(exp));}
}

队列

先进先出(first in first out—FIFO)
队尾插入EnQueue()、队头删除DeQueue()、查询队头Peek()、isEmpty()
应用场景：排队等待的场景，譬如打印机打印
在这里插入图片描述

数组实现队列

front到rear是队列部分。
普通数组会发现rear到了数组末尾后，数组就满了，会有空闲位置。
可以用循环数组（下图只是逻辑视图），数组位置i，下一个位置使用 (i+1)%N，前一个位置为(i+N-1)%N。当i是n-1时，N/N=0，达到循环。
在这里插入图片描述

public class DataStruct {private int[] data;private int front;private int rear;private int capacity;public DataStruct(int capacity) {this.capacity=capacity;this.data=new int[capacity];this.front=-1;this.rear=-1;}public boolean IsEmpty(){if (front==-1&&rear==-1){return true;}return false;}public void enQueue(int x){if (rear==capacity-1) {System.out.println("数组已满");return;}if (rear==-1&&front==-1){front=0;}rear=rear+1;data[rear]=x;}public int deQueue(){if (front==-1&&rear==-1){System.out.println("没有需要删除的元素");return -1;}if (front==rear){front=-1;rear=-1;return data[0];}int x = data[front];front=front+1;return x;}public static void main(String[] args) {DataStruct ds = new DataStruct(3);System.out.println(ds.IsEmpty());ds.enQueue(1);ds.enQueue(2);ds.deQueue();ds.enQueue(3);ds.enQueue(4);}
}

循环数组实现：

public class DataStruct {private int[] data;private int front;private int rear;private int capacity;public DataStruct(int capacity) {this.capacity=capacity;this.data=new int[capacity];this.front=-1;this.rear=-1;}public void enQueue(int x){if ((rear+1)%capacity==front) {System.out.println("数组已满");return;}if (rear==-1&&front==-1){front=0;}rear=(rear+1)%capacity;data[rear]=x;}public int deQueue(){if (front==-1&&rear==-1){System.out.println("没有需要删除的元素");return -1;}if (front==rear){front=-1;rear=-1;return data[0];}int x = data[front];front=(front+1)%capacity;return x;}public static void main(String[] args) {DataStruct ds = new DataStruct(3);ds.enQueue(1);ds.enQueue(2);ds.deQueue();ds.enQueue(3);ds.enQueue(4);ds.enQueue(5);System.out.println(ds.deQueue());}
}

链表实现队列

在这里插入图片描述

class Node {int data;Node next;public Node(int data){this.data = data;this.next = null;}
}
public class DataStruct {private Node front=null;private Node rear=null;public void enQueue(int x){Node temp = new Node(x);if (front == null && rear == null){front=rear=temp;return;}rear.next=temp;rear=temp;return;}public void deQueue(){if (front == null){return;}front=front.next;}public static void main(String[] args) {DataStruct ds = new DataStruct();ds.enQueue(1);ds.enQueue(2);ds.enQueue(3);ds.deQueue();}
}

练习

栈反转链表：图书整理I

http://www.lryc.cn/news/571041.html

相关文章：

  • LangGraph--框架核心思想
  • 3DS MAX三维建模平面基础篇（平面图形的创建和可编辑样条线的使用）
  • 怎样解决虚拟内存不足问题
  • 网站重构技术：XML，XHTML代码规范，样式表调用方式，CSS布局要点
  • 1433,3306,3389端口的利用
  • 经典智能手机诺基亚N78上能用的UCWEB 7.0正式版下载
  • 2010最牛歌曲《郑钱花》——川子
  • 大可乐android 4.3刷机包,大可乐2代MC002线刷刷机教程_大可乐MC002线刷rom系统刷机包...
  • 80x86的汇编器
  • DGL图神经网络库使用大全
  • 属狗的人2012年运程-易久堂风水精准预测
  • Windows网络编程基础
  • 51单片机学习（1）-软件keil下载
  • Nginx超快速入门
  • 复印机维修简明学习教程
  • 递归算法之八皇后问题
  • Aptana_Studio_3_Setup_3.4.0的安装以及环境配置
  • MyEclipse6.5安装maven
  • idea jps使用_必知必会的JVM工具系列一，读懂会用jps、jstat、jinfo、jmap
  • 关于extension_dir
  • 2、Java流程控制：编程界的“逻辑游乐场”
  • qq素材代码_自学三个月的我，利用Python爬虫获取精美素材图片，看看我是怎么做到的（实战篇）...
  • vmware 12 可用 序列号
  • nexus是什么意思android,六年七代八款同使命 看谷歌Nexus成长史
  • 戴尔r63服务器硬盘阵列,dell r720服务器有四块硬盘 raid命令只显示了两块？ - 服务器论坛 - 51CTO技术论坛_中国领先的IT技术社区...
  • 牛腩新闻发布系统——技术总结
  • 使用 XSLT 格式化 XML
  • 著名OJ网址
  • 从零开始构建一个高性能的Web服务器
  • Win32之菜单和库