李沐--动手学深度学习 序列模型
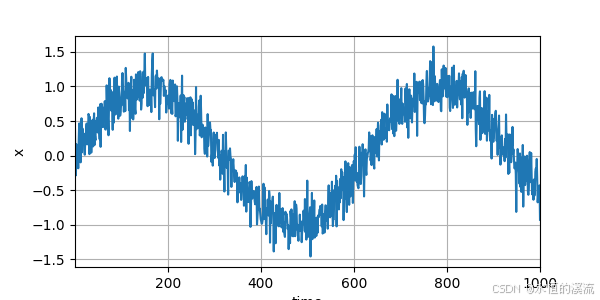
1.使用正弦函数和可加性噪声生成序列数据
import torch
from torch import nn
from d2l import torch as d2l#使用正弦函数和可加性噪声生成序列数据
T = 1000 #总共产生1000个点
time = torch.arange(1,T+1,dtype=torch.float32)
x = torch.sin(0.01*time) + torch.normal(0,0.2,(T,))
d2l.plot(time,[x],'time','x',xlim=[1,1000],figsize=(6,3))
d2l.plt.show()#使用正弦函数和可加性噪声生成序列数据
2.训练
#将这个序列转换为模型的模型的特征-标签对。
#仅使用前600个“特征-标签”对进行训练。
tau = 4
features = torch.zeros((T-tau,tau))
for i in range(tau):features[:,i] = x[i:T-tau+i]
labels = x[tau:].reshape((-1,1))batch_size,n_train = 16,600
#只有前n_train个样本用于训练
train_iter = d2l.load_array((features[:n_train],labels[:n_train]),batch_size,is_train=True)#使用一个相当简单的架构训练模型:一个拥有两个全连接层的多层感知机,ReLU激活函数和平方损失。#初始化网络权重的函数
def init_weight(m):if type(m) == nn.Linear:nn.init.xavier_uniform_(m.weight)#一个简单的多层感知机
def get_net():net = nn.Sequential(nn.Linear(4,10),nn.ReLU(),nn.Linear(10,1))net.apply(init_weight)return net#平方损失。注意:MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')#训练模型.与前面几节(如 3.3节)中的循环训练基本相同
def train(net, train_iter, loss, epochs, lr):trainer = torch.optim.Adam(net.parameters(), lr)for epoch in range(epochs):for X, y in train_iter:trainer.zero_grad()l = loss(net(X), y)l.sum().backward()trainer.step()print(f'epoch {epoch + 1}, 'f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')net = get_net()
train(net, train_iter, loss, 5, 0.01)
d2l.plt.show()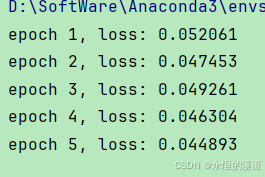
3.预测
(1)一步预测
#检查模型预测下一个时间步的能力, 也就是单步预测
onestep_preds = net(features)
d2l.plot([time,time[tau:]],[x.detach().numpy(),onestep_preds.detach().numpy()],'time','x',legend=['data','1-step preds'],xlim = [1,1000],figsize=(6,3))
d2l.plt.show()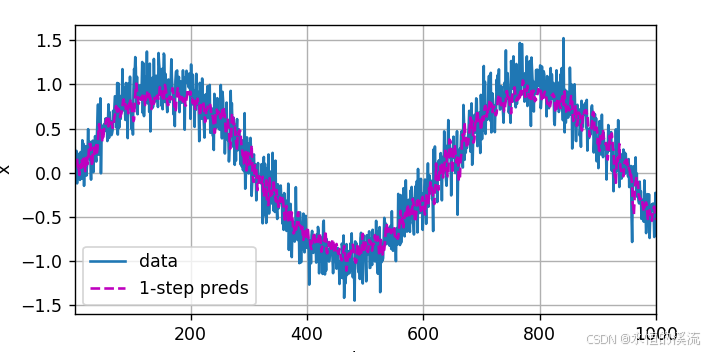
(2)K步预测
#K步预测
multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau,T):multistep_preds[i] = net(multistep_preds[i-tau:i].reshape((1,-1)))
d2l.plot([time,time[tau:],time[n_train+tau:]],[x.detach().numpy(), onestep_preds.detach().numpy(),multistep_preds[n_train+tau:].detach().numpy()],'time','x',legend=['data','1-step preds','multistep preds'],xlim=[1,1000],figsize=(6,3))
d2l.plt.show()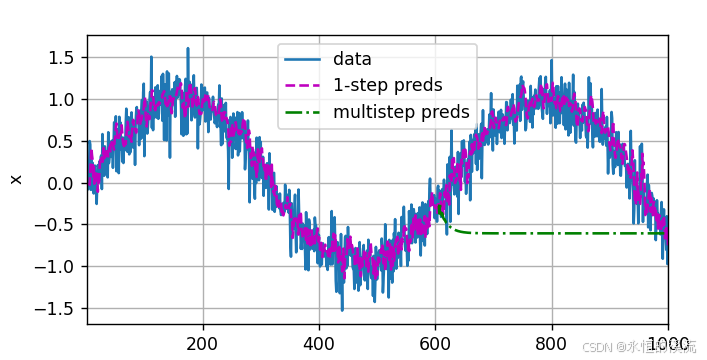
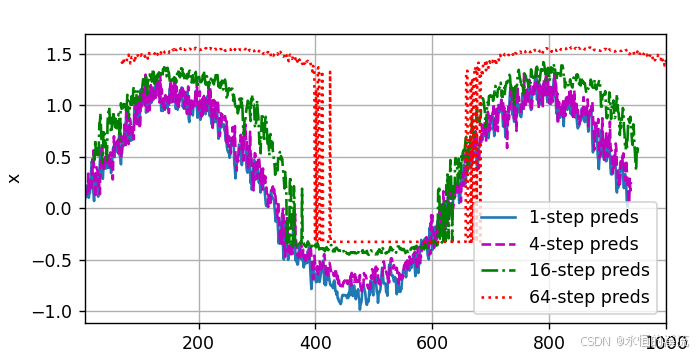
(3)基于k = 1,4,16,64,通过对整个序列预测的计算,更仔细地看一下k步预测的困难。
#基于k = 1,4,16,64,通过对整个序列预测的计算,更仔细地看一下k步预测的困难。
max_steps = 64features = torch.zeros((T-tau-max_steps+1,tau+max_steps))
#列i(i<tau)是来自x的观测,其时间步从(i)到(i+T-tau-max_steps+1)
for i in range(tau):features[:,i] = x[i:i+T-tau-max_steps+1]
# 列i(i>=tau)是来自(i-tau+1)步的预测,其时间步从(i)到(i+T-tau-max_steps+1)
for i in range(tau,tau+max_steps):features[:,i] = net(features[:,i-tau:i]).reshape(-1)steps = (1,4,16,64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],[features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],figsize=(6, 3))
d2l.plt.show()