压电陶瓷换能器导纳圆图公式推导及匹配
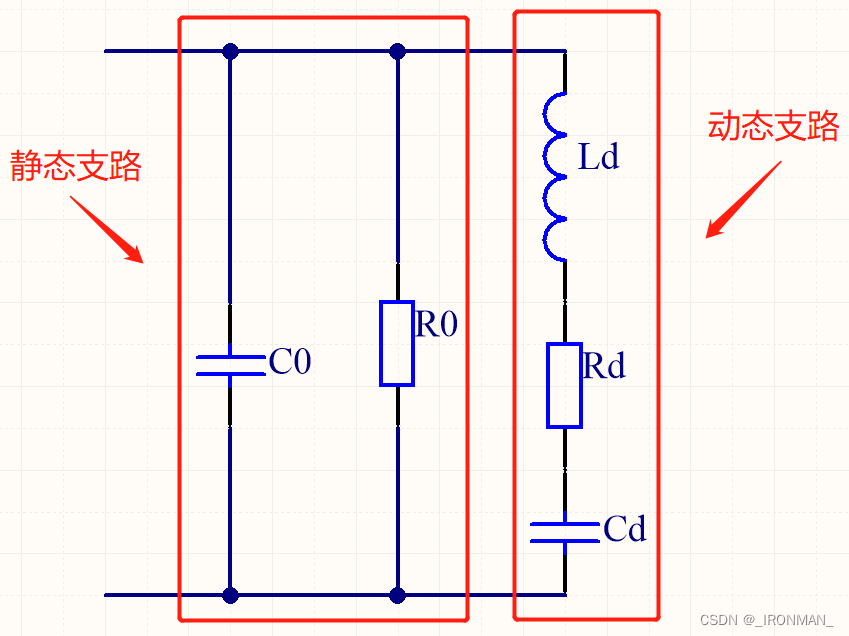
压电陶瓷换能器的等效电路图如下图所示,分为左右两个部分左边的电容和电阻
并联构成了电路的静态支路,
被称为静态电容,可以由电表很方便的测量得到,这部分的参数是由换能器的电学参数决定的。右边的
串联构成了动态支路,这部分参数是由换能器的机械振动参数决定的。
设静态支路的导纳为,动态支路的导纳为
,则总的导纳为
,有
(1)
(2)
设,则有
(3)
(4)
将(3),(4)分别平方后相加,有
(5)
整理一下可得:
(6)
从(6)式可知,将不同角频率下的和
分别为横纵坐标画在二维平面上将得到一个圆。因此可通过测量不同频率下的
和
,通过圆形数据拟合算法(具体方法参考博客平面二维任意椭圆数据拟合算法推导及程序实现详解)即可求解出压电陶瓷的动态电阻
,然而实际能够测量到的是导纳
中的电导
和电纳
,有
(7)
带入式(6)中后可得,
(8)
为已知量,同样的我们依然可以通过关于
和
的圆形数据拟合的算法求解出静态电阻
,和动态电阻
。然后就是要求
,结合式(7)可求得
。将式(4)除以式(3)可得
(9)
整理可得:
(10)
可以看到是一个关于角频率w的二次函数。可以通过简单的抛物线拟合得到参数。
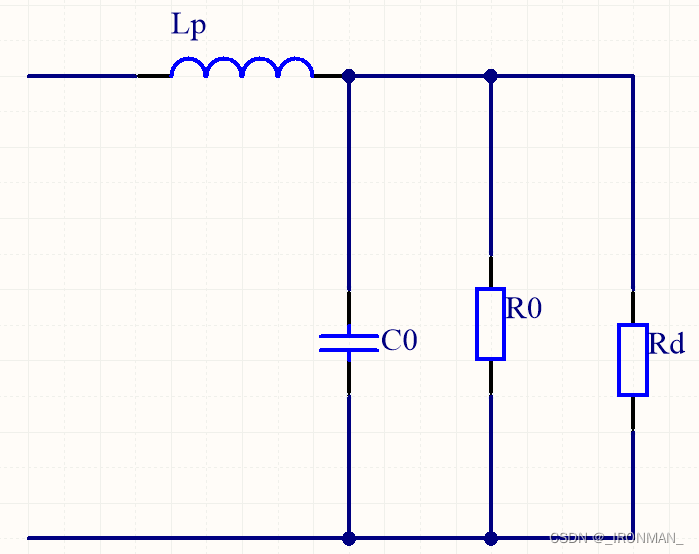
发射或着接收匹配
当换能器处于谐振频率时,其动态支路的等效阻抗只有,且谐振频率为
,此时整个换能器表现出来的是一个容性负载,如下如所示,为了让整个电路呈现出纯阻性则需要串联一个电感
,则此时的阻抗为:
(11)
其虚部应该保持为0,则有,整理可得:
(12)