第四章.误差反向传播法—ReLU/Sigmoid/Affine/Softmax-with-Loss层的实现
第四章.误差反向传播法
4.2 ReLU/Sigmoid/Affine/Softmax-with-Loss层的实现
1.ReLU层
1).公式

2).导数:
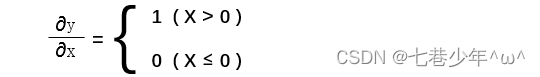
3).计算图:

4).实现:
class ReLU:def __init__(self):self.mask = None# 正向传播def forward(self, x):self.mask = (x <= 0) # 输入值是否≤0,返回值是由True/False构成的Numpy数组out = x.copy()out[self.mask] = 0 # mask中的元素为True的地方置为0return out# 反向传播def backward(self, dout):dout[self.mask] = 0dx = doutreturn dx2.Sigmoid层
1).公式:
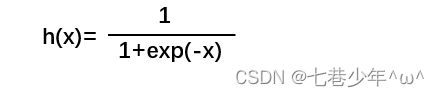
2).计算图:

- 简洁版
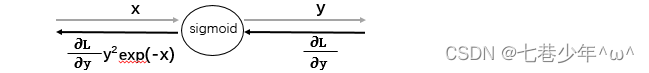
3).导数:

4).实现:
import numpy as npclass Sigmoid:def __init__(self):self.out = None# 正向传播def forward(self, x):out = 1 / (1 + np.exp(-x))self.out = outreturn out# 反向传播def backward(self, dout):dx = dout * (1.0 - self.out) * self.outreturn dx3.Affine层
- 神经网络的正向传播中进行的矩阵乘积运算在几何学领域被称为“仿射变化”,因此,将进行仿射变化的处理实现为Affine层。
- 几何中,仿射变换包括一次线性变换和一次平移,分别对应神经网络的加权和运算和加偏置运算。
1).计算图:
-
单个数据的Affine层:
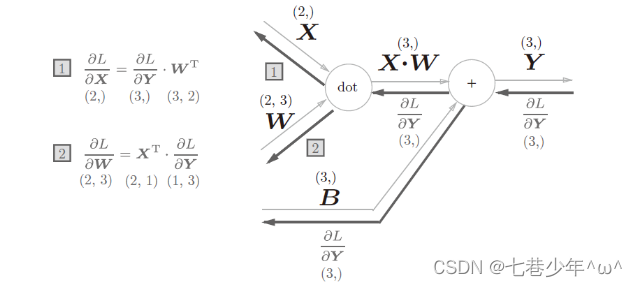
-
批版本的Affine层:
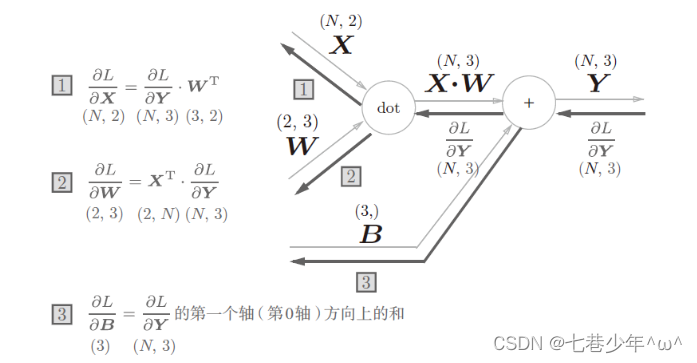
2).实现:
·未考虑输入张量的情况:
import numpy as npclass Affine:def __init__(self, W, b):self.W = Wself.b = bself.x = Noneself.dw = Noneself.db = None# 正向传播def forward(self, x):self.x = xout = np.dot(self.x, self.W) + self.breturn out# 反向传播def backward(self, dout):dx = np.dot(dout, self.W.T)self.dw = np.dot(self.x.T, dout)self.db = np.sum(dout, axis=0)return dx·考虑输入张量的情况 (张量就是多维数据)
import numpy as npclass Affine:def __init__(self, W, b):self.W = Wself.b = bself.x = Noneself.original_x_shape = None# 权重和偏置参数的导数self.dW = Noneself.db = Nonedef forward(self, x):# 对应张量self.original_x_shape = x.shape # 例如:x.shape=(209, 64, 64, 3)x = x.reshape(x.shape[0], -1) # x=(209, 64*64*3)self.x = xout = np.dot(self.x, self.W) + self.breturn outdef backward(self, dout):dx = np.dot(dout, self.W.T)self.dW = np.dot(self.x.T, dout)self.db = np.sum(dout, axis=0)dx = dx.reshape(*self.original_x_shape) # 还原输入数据的形状(对应张量)return dx4.Softmax-with-Loss层
- 神经网络中进行的处理有推理和学习两个阶段,推理阶段通常不适用softmax层,学习阶段需要使用softmax层。
1).计算图:

2).实现:
import numpy as npclass SoftmaxWithLoss:def __init__(self):self.loss = None # 损失self.y = None # softmax的输出self.t = None # 监督数据(one_hot vector)# 输出层函数:softmaxdef softmax(x):if x.ndim == 2:x = x.Tx = x - np.max(x, axis=0)y = np.exp(x) / np.sum(np.exp(x), axis=0)return y.Tx = x - np.max(x) # 溢出对策return np.exp(x) / np.sum(np.exp(x))# 交叉熵误差def cross_entropy_error(y, t):if y.ndim == 1:t = t.reshape(1, t.size)y = y.reshape(1, y.size)# 监督数据是one-hot-vector的情况下,转换为正确解标签的索引if t.size == y.size:t = t.argmax(axis=1)batch_size = y.shape[0]return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size# 正向传播def forward(self, x, t):self.t = tself.y = self.softmax(x)self.loss = self.cross_entropy_error(self.y, self.t)return self.loss# 反向传播def backward(self, dout=1):batch_size = self.t.shape[0]if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况dx = (self.y - self.t) / batch_sizeelse:dx = self.y.copy()dx[np.arange(batch_size), self.t] -= 1dx = dx / batch_sizereturn dx