回归问题的等量分层

一、说明

        在同一个数据集中，我们可以看成是一个抽样体。然而，我们如果将这个抽样体分成两份，每一份依然保留他们的分布（将一个抽样集合合理地分成两个抽样集合），这是我们在训练中经常需要的。在本文中，我将尝试举例说明如何在保留分布比例的情况下对回归问题进行分割。让我们从基础开始。

        您可以在 Kaggle 笔记本上查看工作示例：笔记本

二、什么是分层抽样？

        分层抽样是从数据集中抽取样本，同时保留两个分组（训练和测试）中类别的比例。例如：

        如果我们的数据中有 30% 来自A 类，其余来自B 类；通过分层，我们的训练和测试分割也应该具有相同的比例（例如30%来自A — 70%来自B）。当然，这是一个分类问题的例子，这非常关键，特别是如果我们的数据中存在类别不平衡。如果我们在不使用分层的情况下分割数据，我们可能会得到非常不平衡的分割，这不能正确表示我们模型的泛化能力——或者甚至不给它学习少数类的机会。

三、那么回归又如何呢？

        当我们处理分类问题时，我们的数据中有类别标签，我们现在知道如何处理这种数据。但是回归呢？也许我们可以将这个类别比例定义映射到回归问题的分布比例。如果我们将每个值视为一个单独的类别会怎么样？让我们看看。我们将使用来自Kaggle的“房价竞争”数据。

train_df = pd.read_csv("../input/home-data-for-ml-course/train.csv")
labels = train_df["SalePrice"]
print("Unique label count:", labels.nunique())
print("Data length:", len(train_df), "rows")

Unique label count: 663
Data length: 1460 rows

        如果我们这样做，我们将有663个不同的类别，而我们的数据中只有1460行。这会非常稀疏，我们应该实现一些更聪明的方法。让我们看看标签的分布：

plt.figure(figsize=(12,6))
_ = sns.histplot(data=labels, kde=True, stat="density", bins=30)

        我们有一个右偏分布，如果我们随机分割这些数据，似乎对某些折叠来说会有风险。但让我们尝试将其作为基线。

def fold_visualizer(data, fold_idxs, seed_num):fig, axs = plt.subplots(len(fold_idxs)//2, 2, figsize=(15,(len(fold_idxs)//2)*5))fig.suptitle("Seed: " + str(seed_num), fontsize=16)for fold_id, (train_ids, val_ids) in enumerate(fold_idxs):sns.histplot(data=data[train_ids],kde=True,stat="density",alpha=0.15,label="Train Set",bins=30,line_kws={"linewidth":4},ax=axs[fold_id%(len(fold_idxs)//2), fold_id//(len(fold_idxs)//2)])sns.histplot(data=data[val_ids],kde=True,stat="density", color="darkorange",alpha=0.15,label="Validation Set",bins=30,line_kws={"linewidth":4},ax=axs[fold_id%(len(fold_idxs)//2), fold_id//(len(fold_idxs)//2)])axs[fold_id%(len(fold_idxs)//2), fold_id//(len(fold_idxs)//2)].legend()axs[fold_id%(len(fold_idxs)//2), fold_id//(len(fold_idxs)//2)].set_title("Split " + str(fold_id+1))plt.show()

        让我们使用不同的5个种子创建5 个不同的完全随机 KFold 分割并检查它们：

for i in range(5):baseline_kfold = list(KFold(4,shuffle=True,random_state=i).split(labels))fold_visualizer(data=labels,fold_idxs=baseline_kfold,seed_num=i)

        我们可以明确地看到这些分割的分布差异：

• 种子 0 — 分割 3
• 种子 2 — 分组 2
• 种子 4 — 分组 3

        它们彼此之间差异很大，这种情况可能会导致我们的模型在这些折叠上表现不稳定。让我们为回归数据实现更广义的分层。

四、回归分层（Stratification on Regression）

        正如我们所见，将每个连续值视为单独的类别并不明智。但我们可以使用分箱对它们进行分组。我们可以将标签分成k 个大小相等的区间，并将每个区间定义为一个唯一的类。这里，k是我们应该为我们的问题设置的超参数。

def create_cont_folds(df, n_s=8, n_grp=1000, seed=1):skf = StratifiedKFold(n_splits=n_s, shuffle=True, random_state=seed)grp = pd.qcut(df, n_grp, labels=False)target = grpfold_nums = np.zeros(len(df))for fold_no, (t, v) in enumerate(skf.split(target, target)):fold_nums[v] = fold_nocv_splits = []for i in range(num_of_folds):test_indices = np.argwhere(fold_nums==i).flatten()train_indices = list(set(range(len(labels))) - set(test_indices))cv_splits.append((train_indices, test_indices))return cv_splits

我们只需使用pandas库中的.cut()函数即可。它会通过查找数据的最小值和最大值将数据分成相等的间隔。由于我们的分布是偏斜的，我认为使用基于分位数的分箱是有风险的。如果您认为您的分布适合这样做，您可以简单地将.cut()更改为.qcut()。

让我们看看当我们使用分层连续分裂时我们会得到什么：

num_of_folds = 4
num_of_groups = 100for i in range(5):cv_splits = create_cont_folds(labels, n_s=num_of_folds, n_grp=num_of_groups, seed=i)fold_visualizer(data=labels,fold_idxs=cv_splits,seed_num=i)

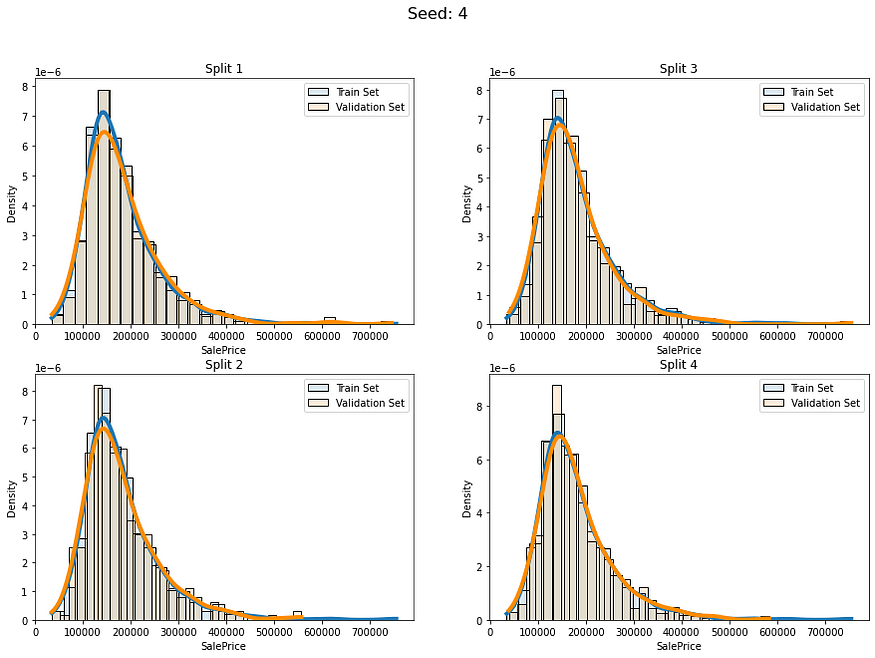
        似乎我们避免了以不同的分布比例拆分数据。我们仍然有差异，但我认为这是可以接受的，因为我们的数据只有约1000行。

        这就是为回归问题生成分层折叠的全部内容！这确实是一种实现我们想要的结果的简单方法，当然，我们可能会尝试实施不同的方法来实现它。