循环对称复高斯分布(Circularly Symmetric Complex Gaussian Distribution)
一、引言
循环对称复高斯分布(Circularly Symmetric Complex Gaussian Distribution,简称CSCG)在无线通信、信号处理等领域具有广泛的应用。作为一种特殊的复高斯分布,CSCG具有独特的性质,如循环对称性、高斯性等,这使得它在描述无线通信系统中的噪声、信号等方面具有独特的优势。这里主要从定义、表达式、性质及主要应用等方面对CSCG进行详细介绍,并给出示例展示其生成和作用方式。
二、定义
循环对称复高斯分布是指复随机变量Z=X+iY(其中X和Y分别为实部和虚部)的实部和虚部都是独立同分布的零均值高斯随机变量,并且具有相同的方差σ²。这种分布具有循环对称性,即对于任意实数θ,e^(jθ)Z仍然服从相同的分布。对于循环对称复高斯分布Z~CN(0,σ²),其概率密度函数可以表示为:

其中,|z|表示复数z的模。
三、性质
- 循环对称性:
循环对称性是CSCG分布最显著的特点之一。对于任意实数θ,e^(jθ)Z仍然服从CSCG分布,即其分布不随相位的旋转而改变。这一性质使得CSCG分布在描述无线通信系统中的旋转不变性方面具有独特的优势。
2. 高斯性:
CSCG分布的实部和虚部都是独立同分布的高斯随机变量。这一性质使得CSCG分布在数学处理上具有简便性,可以利用高斯分布的相关性质进行推导和分析。
3. 功率谱密度平坦:
在通信系统中,CSCG噪声的功率谱密度在整个频率范围内是平坦的。这意味着其自相关函数在t=0时为Dirac-delta函数,即噪声在时间上是不相关的。这一性质使得CSCG噪声在通信系统建模中具有广泛的应用。
4. 模的平方服从指数分布:
对于CSCG分布的随机变量Z,其模的平方|Z|²服从参数为σ²/2的指数分布。这一性质在通信系统的性能分析中具有重要意义,可以用于推导系统的误码率、数据传输速率等性能指标。
四、主要应用
- 无线通信系统中的噪声建模:
在无线通信系统中,噪声是影响系统性能的重要因素之一。CSCG分布作为无线通信系统中噪声的主要分布形式之一,可以用于描述接收端接收到的噪声信号。通过模拟CSCG噪声,可以评估系统在不同噪声条件下的性能表现。
2. 信号检测与估计:
在无线通信系统中,信号检测与估计是实现高效通信的关键技术之一。利用CSCG分布的性质,可以推导出信号检测与估计的相关算法,如最大似然估计、最小均方误差估计等。这些算法在提高系统的数据传输速率和降低误码率方面具有重要作用。
3. 智能反射面(IRS)辅助的通信系统:
IRS是一种新型的无线通信技术,通过调整反射面的相位和幅度来改变无线信号的传播路径。在IRS辅助的通信系统中,接收到的信号包括直接路径的信号和经过IRS反射的信号。这些信号都会受到CSCG噪声的影响。通过优化IRS的反射系数和发射功率,可以最大化接收信号的信噪比(SNR),从而提高系统的性能。
4. 雷达系统中的目标检测:
在雷达系统中,目标检测是实现目标跟踪和识别的关键步骤之一。CSCG分布可以用于描述雷达接收到的回波信号中的噪声部分。通过利用CSCG分布的性质,可以推导出目标检测的相关算法,如恒虚警率检测(CFAR)等。这些算法在提高雷达系统的目标检测性能和降低虚警率方面具有重要作用。
五、MATLAB代码示例
这里以一个MATLAB代码示例,用于生成循环对称复高斯分布的随机变量并展示其作用方式。
% MATLAB代码示例:生成循环对称复高斯分布的随机变量
clc;
clear;
close all;
% 设置参数
mu_real = 0; % 实部均值
mu_imag = 0; % 虚部均值
sigma_squared = 1; % 方差
num_samples = 1000; % 样本数
% 生成实部和虚部的高斯随机变量
real_part = mu_real + sqrt(sigma_squared/2) * randn(num_samples, 1);
imag_part = mu_imag + sqrt(sigma_squared/2) * randn(num_samples, 1);
% 组合成复随机变量
complex_samples = real_part + 1i * imag_part;
% 绘制复随机变量的实部和虚部
figure;
subplot(2,1,1);
histogram(real_part, 'Normalization', 'pdf');
title('实部的高斯分布');
xlabel('实部值');
ylabel('概率密度');
grid on
subplot(2,1,2);
histogram(imag_part, 'Normalization', 'pdf');
title('虚部的高斯分布');
xlabel('虚部值');
ylabel('概率密度');
grid on
% 绘制复随机变量的模的平方分布
figure;
histogram(abs(complex_samples).^2, 'Normalization', 'pdf', 'BinWidth', 0.1);
title('复随机变量的模的平方分布');
xlabel('模的平方值');
ylabel('概率密度');
grid on
% 验证模的平方服从指数分布
% 计算理论上的指数分布概率密度函数
x = linspace(0, 10, 1000);
pdf_exponential = (1/(sigma_squared/2)) * exp(-x/(sigma_squared/2));
% 绘制理论上的指数分布概率密度函数与仿真结果的对比
figure;
hold on;
histogram(abs(complex_samples).^2, 'Normalization', 'pdf', 'BinWidth', 0.1);
plot(x, pdf_exponential, 'r-', 'LineWidth', 2);
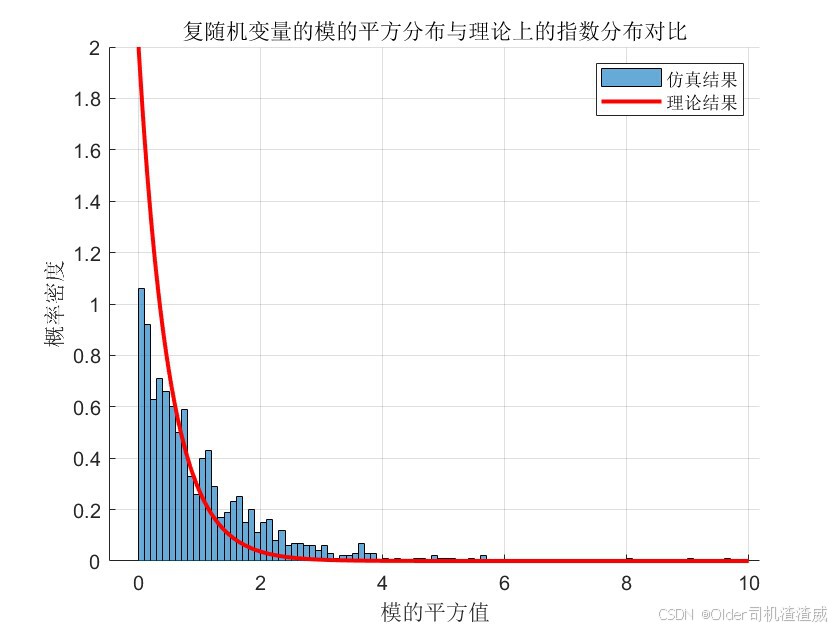
title('复随机变量的模的平方分布与理论上的指数分布对比');
xlabel('模的平方值');
ylabel('概率密度');
legend('仿真结果', '理论结果');
grid on
hold off;
基本步骤
- 设置参数:
首先,设置了实部和虚部的均值(mu_real和mu_imag)为0,方差(sigma_squared)为1,以及样本数(num_samples)为1000。
2. 生成实部和虚部的高斯随机变量:
利用randn函数生成服从标准正态分布的随机变量,然后乘以sqrt(sigma_squared/2)进行缩放,使其方差为σ²/2。这样生成的实部和虚部就是独立同分布的零均值高斯随机变量。
3. 组合成复随机变量:
将生成的实部和虚部相加,得到复随机变量。
4. 绘制实部和虚部的高斯分布:
利用histogram函数绘制实部和虚部的高斯分布直方图,并设置归一化为概率密度。通过对比可以看出,实部和虚部都服从高斯分布。
5. 绘制复随机变量的模的平方分布:
利用histogram函数绘制复随机变量的模的平方分布直方图。通过对比可以看出,模的平方服从指数分布。
6. 验证模的平方服从指数分布:
计算理论上的指数分布概率密度函数,并将其与仿真结果进行对比。通过对比可以看出,仿真结果与理论结果基本一致,验证了模的平方服从指数分布的性质。


六、结论
循环对称复高斯分布在无线通信、信号处理等领域具有广泛的应用。本文详细介绍了CSCG的定义、表达式、性质及主要应用,并给出了代码示例展示其生成和作用方式。通过学习,可以深入理解CSCG分布的性质和应用,为后续的研究和工程实践提供有力支持。
