【C++习题】17.二分查找算法_二分查找
文章目录
- 二分查找算法简介
- 题目链接:
- 题目描述:
- 解法
- C 算法代码:
- 图解
- 总结朴素二分模板
二分查找算法简介
特点:
二分查找算法,是最恶心,细节最多,最容易写出死循环的算法。(而且非常难调试)
不过如果真的掌握了二分算法后,会觉得这个是最简单的算法。
学习中的侧重点:
算法原理:
一开始会觉得只有数组有序的情况才能使用二分算法
但是学到后面,会发现就算无序,只要有规律也可以使用二分算法
模板:
不要死记硬背,需要理解背后的原理,做到理解后再记忆。
会讲
3个模板
- 朴素的二分模板
- 查找左边界的二分模板
- 查找右边界的二分模板
3个模板加起来不超过20行,可以解决99.99%的二分题,但不能只背模板。
下面的一题会讲到第一个模板,后一题会讲第二第三个模板。
朴素的二分模板,朴素意味着简单,只有一些非常简单的二分题才用到。
查找左边界的二分模板和查找右边界的二分模板是万能的,也就是朴素模板可以解决的也可以用另外两个解决,不过细节很多。
题目链接:
leetcode 704.二分查找
题目描述:

解法
暴力解法:
遍历一遍,时间复杂度O(n)
例如:
[1,2,3,4,5,6,7,8],t=5比如
4,4比t小,那么它前面的比4还小,那么全比t小,可以把4和4之前的数全干掉。同理,
6和6后面的数也一样可以干掉。总的来说就是,随便找个端点,只要不是目标值,那么它的一侧可以全部干掉。
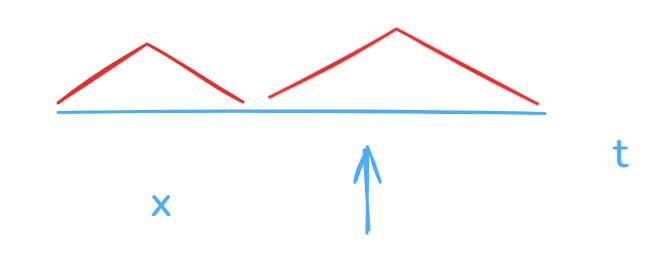
总结来说就是:二段性
就是当我们发现一个规律,然后根据这个规律选取某一个点能把这个数组分成两部分,然后根据规律可以有选择的舍去一部分,进而在另一部分里面继续查找的时候,就可以使用二分查找算法。
注意上面的描述,不管有序无序,只要有二段性都可以使用二分算法。
对于端点的选择,我们可以选择
1/2处,1/3处,1/4处等等。我们的目的是找到二段性。
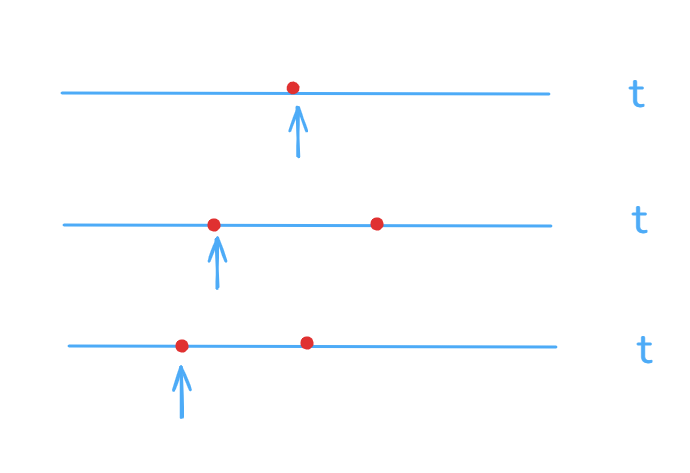
所以端点的选择比较多,但是我们一般选
1/2的点。在概率学里面是求数学期望。就像
1/3处的点,虽然可能直接把2/3的部分抹除,但是也可能只抹除了1/3。在这么多的端点的划分里面,选择中间这个点的时间复杂度是最好的。
我们可以定义一个
left指针,right指针和mid指针
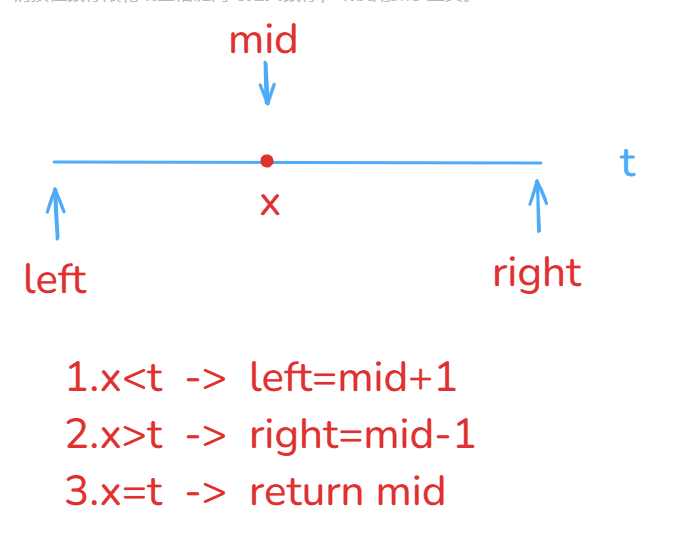
这
3步就是朴素二分算法的核心了。细节问题:
循环结束的条件是什么?
left>right的时候结束循环
left<=right的时候一直循环为什么是正确的?
通过二段性达到和暴力解法一样的排除作用
为什么时间复杂度快?
log2n
C 算法代码:
int search(int* nums, int numsSize, int target)
{// 初始化 left 与 right 指针int left = 0, right = numsSize - 1;// 由于两个指针相交时,当前元素还未判断,因此需要取等号while (left <= right){// 先找到区间的中间元素int mid = left + (right - left) / 2;// 分三种情况讨论if (nums[mid] == target) return mid;else if (nums[mid] > target) right = mid - 1;else left = mid + 1;}// 如果程序走到这里,说明没有找到目标值,返回 -1return -1;
}
图解
例如:[1,2,3,4,5,6,7,8],t=5
-
left = 0, right =7left <= right进入循环mid=0+(7-0)/2=3
nums[mid]=4<t满足
else条件,执行left = mid + 1=4 -
left = 4, right =7left <= right进入循环mid=4+(7-4)/2=5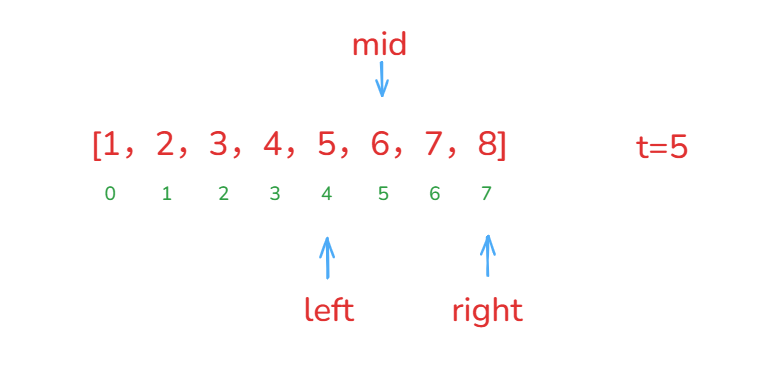
nums[mid]=6>t满足
nums[mid] > target条件,执行right = mid - 1=4 -
left = 4, right =4left <= right进入循环mid=4+(4-4)/2=4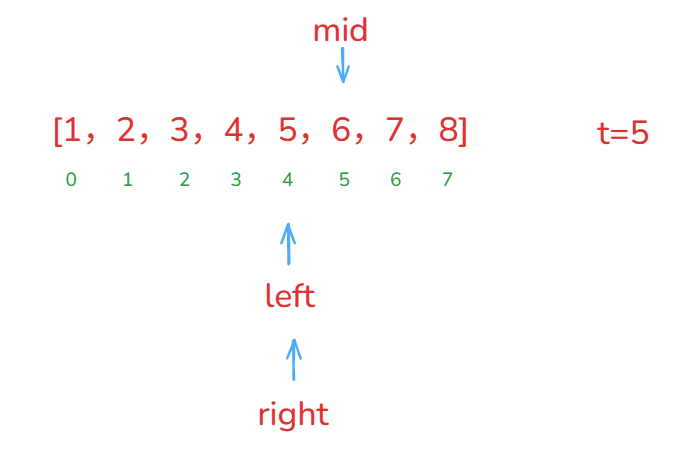
满足
nums[mid] == target)条件,执行return mid;
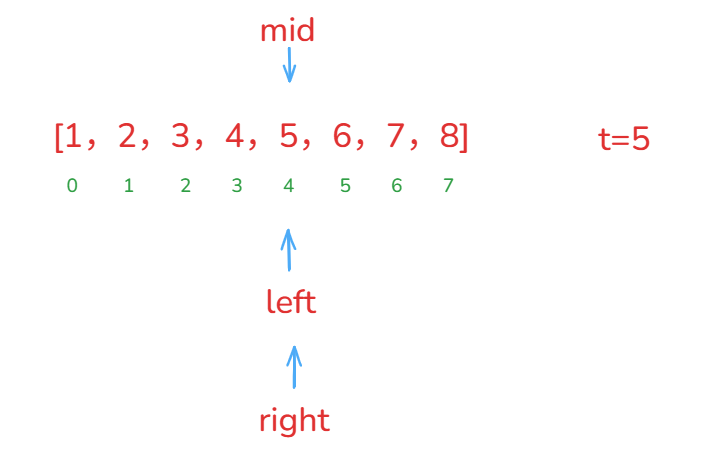
- 程序结束。
总结朴素二分模板
while(left <= right){int mid = left + (right - left) / 2;//int mid = left + (right - left + 1) / 2;//这两个在朴素版本作用一样if(......)left = mid + 1;else if(......)right = mid - 1;elsereturn ......;
}
