当前位置：首页 > news >正文

探索空间自相关：揭示地理数据中的隐藏模式

news 2025/8/3 8:39:48

一、什么是空间自相关？

类型

二、空间自相关的数学基础

空间加权矩阵

三、度量空间自相关的方法

1. 全局自相关

2. 局部自相关

四、空间自相关的实际应用

五、Python实现空间自相关分析

1. 数据准备

2. 计算莫兰指数

3. 局部自相关（LISA 分析）

六、总结

本文将详细介绍空间自相关的概念、数学基础、常见的度量方法及实际应用，最后通过Python代码展示如何进行空间自相关分析。

一、什么是空间自相关？

空间自相关用来衡量地理空间中数据值的相似性或相关性。它的核心思想是：“相邻地区的事物往往更相似”。这一思想来源于托布勒的第一地理学定律（Tobler's First Law of Geography）：

“一切事物都是相关的，但近的事物比远的事物更相关。”

类型

正空间自相关：相邻区域具有相似的值。例如，城市中的富人区与相邻地区的收入水平通常较高。
负空间自相关：相邻区域具有相反的值。例如，工业区与周围居民区的空气质量可能存在负相关。
无空间自相关：空间分布随机，没有明确的模式。

二、空间自相关的数学基础

空间自相关通过“空间加权矩阵（Spatial Weight Matrix）”和统计方法进行量化。

空间加权矩阵 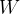$W$

用于定义区域之间的空间关系，常见方式包括：
1. 邻接矩阵：两个区域是否直接相邻。
2. 距离矩阵：两个区域之间的地理距离。
3. K最近邻矩阵：基于最近的 $k$ 个邻居。

一个常见的矩阵形式是 $W_{ij} = 1$ （如果区域 $i$ 和 $j$ 相邻），否则 $W_{ij} = 0$ 。

三、度量空间自相关的方法

1. 全局自相关

全局指标用于衡量整个研究区域的自相关性。

莫兰指数（Moran’s I）

莫兰指数是最常用的全局空间自相关指标，其公式为：

$I = \frac{N \sum_{i} \sum_{j} W_{ij} (x_i - \bar{x})(x_j - \bar{x})}{\sum_{i} (x_i - \bar{x})^2 \sum_{i} \sum_{j} W_{ij}}$

$N$ ：样本数量
$x_i$ ：第 iii 个区域的观测值
$\bar{x}$ ：观测值的平均值
$W_{ij}$ ：空间权重

取值范围：

$I > 0$ ：正自相关
$I < 0$ ：负自相关
$I = 0$ ：无自相关
Geary's C 另一个全局指标，敏感于局部差异。

2. 局部自相关

局部指标用于分析具体区域的自相关性。

局部莫兰指数（LISA） 局部莫兰指数用来检测局部热点（hotspot）或冷点（coldspot）。

$I_i = \frac{x_i - \bar{x}}{s^2} \sum_{j} W_{ij} (x_j - \bar{x})$

Getis-Ord Gi*指数 用来识别空间中具有统计显著性的热点和冷点。

四、空间自相关的实际应用

城市规划
- 分析城市热岛效应分布，指导绿色区域规划。
- 房地产价格分布模式识别，优化土地利用。
生态与环境
- 森林分布的空间格局分析，发现生态敏感区域。
- 空气质量的空间分布，找出污染热点。
流行病学
- 传染病的空间扩散研究，识别疫情的聚集区。
社会经济分析
- 贫富差距、犯罪率等的空间分布分析。

五、Python实现空间自相关分析

以下是使用 pysal 库进行莫兰指数计算的示例：

1. 数据准备

安装必要库：

pip install pysal geopandas

加载空间数据：

import geopandas as gpd
from pysal.lib.weights.contiguity import Queen
from pysal.explore.esda.moran import Moran
import matplotlib.pyplot as plt# 加载地理数据（以 GeoJSON 文件为例）
data = gpd.read_file("data.geojson")# 选取分析变量
variable = data["population_density"]# 生成邻接矩阵（基于 Queen 邻接规则）
weights = Queen.from_dataframe(data)
weights.transform = 'r'

2. 计算莫兰指数

# 计算全局莫兰指数
moran = Moran(variable, weights)
print(f"Moran's I: {moran.I}, p-value: {moran.p_sim}")

3. 局部自相关（LISA 分析）

from pysal.explore.esda.moran import Moran_Local# 计算局部莫兰指数
lisa = Moran_Local(variable, weights)# 可视化 LISA 热点
data["LISA"] = lisa.q
data.plot(column="LISA", legend=True, cmap="coolwarm")
plt.title("LISA Cluster Map")
plt.show()