CF862B Mahmoud and Ehab and the bipartiteness(二分图的性质)
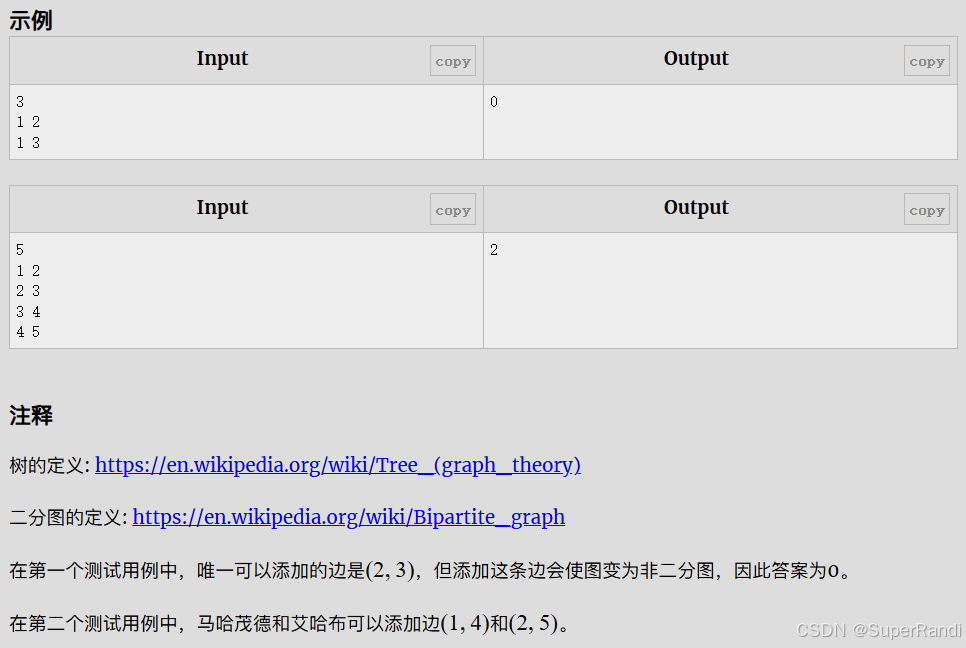
思路:一个二分图是由两个集合组成的,同一个集合中的节点间不能连边,所以一个二分图最多有cnt[1]*cnt[2]条边,题目给出一个树的n-1条边,要我们添加最多的边数使他成为二分图,添加的边数就是cnt[1]*cnt[2]-n+1条,所以我们先用dfs对每个节点进行染色,计算出两个个集合的节点数
Code:
constexpr int N=2e5+5,mod=1e9+7;int n;
int h[N],e[N],ne[N],idx;
int color[N],cnt[4];void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}void dfs(int u,int c)
{color[u]=c;cnt[c]++;for(int i=h[u];~i;i=ne[i]){if(!color[e[i]]) dfs(e[i],3-c);}}void solve()
{ cin>>n;memset(h,-1,sizeof h);for(int i=1;i<=n;i++){int a,b;cin>>a>>b;add(a,b),add(b,a);} dfs(1,1);int sum=cnt[1]*cnt[2];cout<<sum-n+1;
}