当前位置：首页 > news >正文

DAY64||dijkstra（堆优化版）精讲 ||Bellman_ford 算法精讲

news 2025/7/2 6:12:51

dijkstra（堆优化版）精讲

题目如上题47. 参加科学大会（第六期模拟笔试）

邻接表

本题使用邻接表解决问题。

邻接表的优点：

对于稀疏图的存储，只需要存储边，空间利用率高
遍历节点链接情况相对容易

缺点：

检查任意两个节点间是否存在边，效率相对低，需要 O(V)时间，V表示某节点链接其他节点的数量。
实现相对复杂，不易理解

节点1 指向节点3 权值为 1
节点1 指向节点5 权值为 2
节点2 指向节点4 权值为 7
节点2 指向节点3 权值为 6
节点2 指向节点5 权值为 3
节点3 指向节点4 权值为 3
节点5 指向节点1 权值为 10

这样我们就把图中权值表示出来了。

但是在代码中使用 pair<int, int> 很容易让我们搞混了，导致代码可读性很差。

那么可以定一个类 EDGE来取代 pair<int, int>

堆优化三部曲

1.选源点到哪个节点近且该节点未被访问过，我们需要一个 小顶堆 来帮我们对边的权值排序，每次从小顶堆堆顶取边就是权值最小的边。

2.该最近节点被标记访问过，和朴素版一样

3.更新非访问节点到源点的距离

和朴素版区别

邻接表的表示方式不同
使用优先级队列（小顶堆）来对新链接的边排序

代码

堆优化的时间复杂度只和边的数量有关和节点数无关，在优先级队列中放的也是边。

#include <iostream>
#include <vector>
#include<list>
#include<queue>
#include <climits>
using namespace std;
class mycomparison//小顶堆比较器
{public://重载 () 操作符，比较两个 pair<int, int> 的第二个元素，//返回 lhs.second > rhs.second，使得优先队列按第二个元素从小到大排序。bool operator()(const pair<int,int>&lhs,const pair<int,int>&rhs){return lhs.second>rhs.second;}};
struct Edge
{int to;//邻接顶点int val;//边的权值Edge(int t,int v):to(t),val(v){}//构造函数};int main() {int n,m,p1,p2,val;//公共汽车站数量，公路数量，某站到某站及其所花时间cin>>n>>m;vector<list<Edge>>grid(n+1);//每个元素是一个链表 list<Edge>，用于存储图的邻接表。//读取并填充邻接表for(int i=0;i<m;i++){cin>>p1>>p2>>val;grid[p1].push_back(Edge(p2,val));//将边 p1 到 p2 的信息添加到 grid[p1] 中。}int start=1;int end=n;//初始点和终点vector<int>minDist(n+1,INT_MAX);//存储从起始点到每个节点的最短距离vector<bool>visited(n+1,false);minDist[start]=0;//初始点到自身的距离是0//声明一个优先队列 pq，元素类型为 pair<int, int>，使用 mycomparison 作为比较器，实现小顶堆。priority_queue<pair<int,int>,vector<pair<int,int>>,mycomparison>pg;pg.push(pair<int,int>(start,0));//将起始点及其距离0加入优先队列。//dijkstra算法核心while(!pg.empty()){// <节点， 源点到该节点的距离>// 1、选距离源点最近且未访问过的节点pair<int,int>cur=pg.top();pg.pop();if(visited[cur.first])continue;visited[cur.first]=true;//2.标记该节点已被访问//3.更新非访问节点到源点的距离//遍历当前节点 cur.first 指向的所有邻接节点 edge。for(Edge edge:grid[cur.first]){//如果邻接节点 edge.to 未被访问且通过当前节点 cur.first 到达 edge.to 的距离更短，则更新if(!visited[edge.to]&&minDist[cur.first]+edge.val<minDist[edge.to]){minDist[edge.to]=minDist[cur.first]+edge.val;//将邻接节点 edge.to 及其新的距离加入优先队列。pg.push(pair<int,int>(edge.to,minDist[edge.to]));}}}if(minDist[end]==INT_MAX)cout<<-1<<endl;//无法到达目标elsecout<<minDist[end]<<endl;//到达终点的最短路径}

模拟运行结果
4 4
1 2 1
1 3 4
2 3 1
3 4 1
首先读取 n=4 和 m=4，初始化邻接表 grid。

读取边并填充邻接表：

边 (1, 2, 1)，grid[1].push_back(Edge(2, 1))
边 (1, 3, 4)，grid[1].push_back(Edge(3, 4))
边 (2, 3, 1)，grid[2].push_back(Edge(3, 1))
边 (3, 4, 1)，grid[3].push_back(Edge(4, 1))

初始化 minDist 和 visited。

初始化优先队列，将起始点及其距离0加入优先队列。

运行 Dijkstra 算法：

第一次迭代：从优先队列中取出节点1，更新 minDist 为 [0, 1, 4, INT_MAX]，并将节点2和3加入优先队列。
第二次迭代：从优先队列中取出节点2，更新 minDist 为 [0, 1, 2, INT_MAX]，并将节点3加入优先队列。
第三次迭代：从优先队列中取出节点3，更新 minDist 为 [0, 1, 2, 3]，并将节点4加入优先队列。
第四次迭代：从优先队列中取出节点4，minDist 保持不变。
3

Bellman_ford 算法精讲

94. 城市间货物运输 I

题目描述

某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。

网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。

请找出从城市 1 到城市 n 的所有可能路径中，综合政府补贴后的最低运输成本。如果最低运输成本是一个负数，它表示在遵循最优路径的情况下，运输过程中反而能够实现盈利。

城市 1 到城市 n 之间可能会出现没有路径的情况，同时保证道路网络中不存在任何负权回路。

输入描述

第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。

接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v （单向图）。

输出描述

如果能够从城市 1 到连通到城市 n，请输出一个整数，表示运输成本。如果该整数是负数，则表示实现了盈利。如果从城市 1 没有路径可达城市 n，请输出 "unconnected"。

输入示例
6 7
5 6 -2
1 2 1
5 3 1
2 5 2
2 4 -3
4 6 4
1 3 5
输出示例
1
提示信息

示例中最佳路径是从 1 -> 2 -> 5 -> 6，路上的权值分别为 1 2 -2，最终的最低运输成本为 1 + 2 + (-2) = 1。

示例 2：

4 2
1 2 -1
3 4 -1

在此示例中，无法找到一条路径从 1 通往 4，所以此时应该输出 "unconnected"。

数据范围：

1 <= n <= 1000；
1 <= m <= 10000;

-100 <= v <= 100;

本题依然是单源最短路问题，求从节点1 到节点n 的最小费用。 但本题不同之处在于边的权值是有负数了。

Bellman_ford算法的核心思想是对所有边进行松弛n-1次操作（n为节点数量），从而求得目标最短路。

what is 松弛（核心）

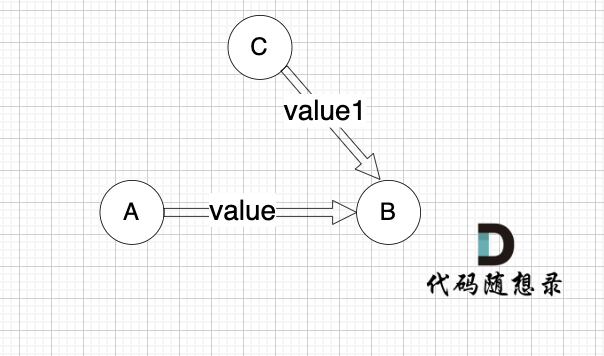
例如一条边，节点A 到节点B 权值为value，如图：

minDist[B] 表示到达B节点最小权值，minDist[B] 有哪些状态可以推出来？

状态一： minDist[A] + value 可以推出 minDist[B]

状态二： minDist[B]本身就有权值（可能是其他边链接的节点B 例如节点C，以至于 minDist[B]记录了其他边到minDist[B]的权值）

minDist[B] 应为如何取舍。

本题我们要求最小权值，那么这两个状态我们就取最小的
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
也就是说，如果通过 A 到 B 这条边可以获得更短的到达B节点的路径，即如果 minDist[B] > minDist[A] + value，那么我们就更新 minDist[B] = minDist[A] + value ，这个过程就叫做 “松弛” 。

Bellman_ford算法也是采用了动态规划的思想，即：将一个问题分解成多个决策阶段，通过状态之间的递归关系最后计算出全局最优解。

为什么松弛“n-1”次

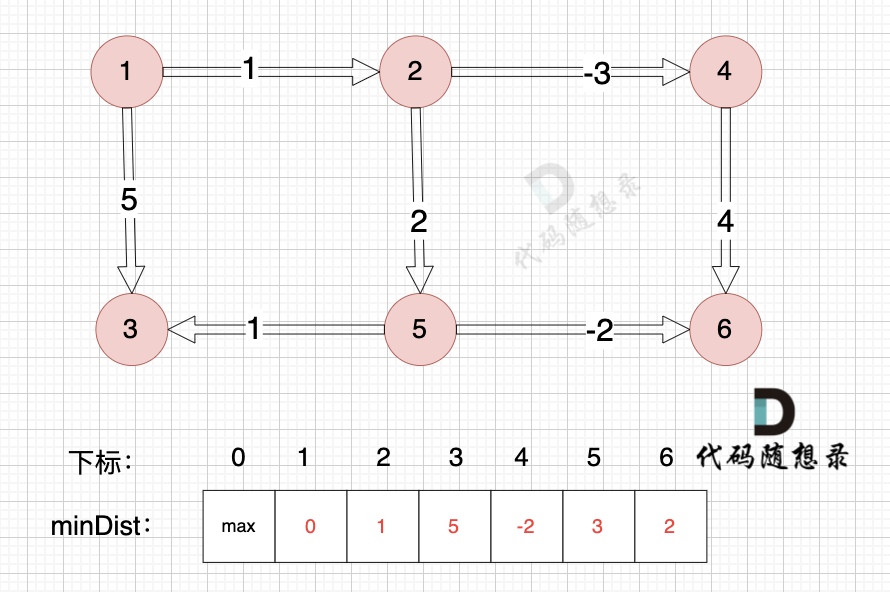
以上是对所有边进行一次松弛之后的结果。

那么需要对所有边松弛几次才能得到起点（节点1）到终点（节点6）的最短距离呢？

对所有边松弛一次，相当于计算起点到达与起点一条边相连的节点的最短距离。

节点数量为n，那么起点到终点，最多是 n-1 条边相连。

那么无论图是什么样的，边是什么样的顺序，我们对所有边松弛 n-1 次就一定能得到起点到达终点的最短距离。

其实也同时计算出了，起点到达所有节点的最短距离，因为所有节点与起点连接的边数最多也就是 n-1 条边。

代码

#include<iostream>
#include<vector>
#include<climits>
using namespace std;
int main()
{int n,m,p1,p2,val;//节点数、边数、边的两个节点和边的权重。cin>>n>>m;vector<vector<int>>grid;for(int i=0;i<m;i++)//每条边用一个包含三个整数的向量表示。{cin>>p1>>p2>>val;grid.push_back({p1,p2,val});}int start=1;int end=n;vector<int>minDist(n+1,INT_MAX);minDist[start]=0;//Bellman-Ford 算法核心for(int i=1;i<n;i++)//对所有边松弛一次{for(vector<int>&side:grid)//每次松弛，都是对所有边松弛一次{int from=side[0];//边的出发点int to=side[1];//边的到达点int price=side[2];//边的权值//松弛操作//minDist[from] != INT_MAX 防止从未计算过的节点出发if(minDist[from]!=INT_MAX&&minDist[to]>minDist[from]+price){//且通过当前边到达点的最短距离可以更新，则进行更新minDist[to]=minDist[from]+price;}}}if(minDist[end]==INT_MAX)cout<<"unconnected"<<endl;else cout<<minDist[end]<<endl;//到达终点最短路径}

模拟运行结果

假设输入如下：
4 4
1 2 1
1 3 4
2 3 1
3 4 1
首先读取 n=4 和 m=4，初始化边的存储 grid。

读取边并存储在 grid 中：

边 (1, 2, 1)，grid.push_back({1, 2, 1})
边 (1, 3, 4)，grid.push_back({1, 3, 4})
边 (2, 3, 1)，grid.push_back({2, 3, 1})
边 (3, 4, 1)，grid.push_back({3, 4, 1})

初始化 minDist，设置 minDist[start] = 0。

运行 Bellman-Ford 算法：

第一次松弛：
处理边 (1, 2, 1)，更新 minDist[2] = 1。
处理边 (1, 3, 4)，更新 minDist[3] = 4。
处理边 (2, 3, 1)，更新 minDist[3] = 2。
处理边 (3, 4, 1)，更新 minDist[4] = 3。
第二次松弛：
处理边 (1, 2, 1)，minDist[2] 保持不变。
处理边 (1, 3, 4)，minDist[3] 保持不变。
处理边 (2, 3, 1)，minDist[3] 保持不变。
处理边 (3, 4, 1)，minDist[4] 保持不变。
第三次松弛：
处理边 (1, 2, 1)，minDist[2] 保持不变。
处理边 (1, 3, 4)，minDist[3] 保持不变。
处理边 (2, 3, 1)，minDist[3] 保持不变。
处理边 (3, 4, 1)，minDist[4] 保持不变。
最终输出：
3