计算两个结构的乘法
在行列可自由变换的平面上,2点结构有3个
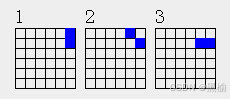
3点结构有6个
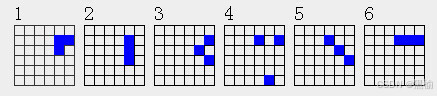
计算2*2
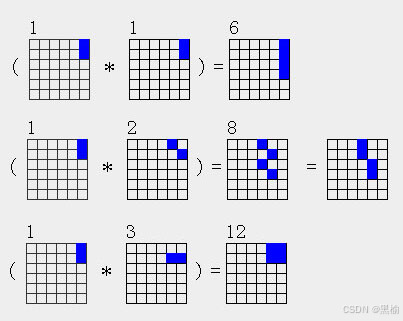
| 2a1*2a1=4a6 |
| 2a1*2a2=4a8 |
| 2a1*2a3=4a12 |
显然2a1*2a1=4a6因为这3个结构都分布在同一列上,就是整数乘法。2a1*2a2的结果有2种写法,一种外形像2a1细节为2a2,一种外形为2a2,细节为2a1.但这两个结构是相同的,所以可以被分解成两个结构积的结构有一种外形和细节的2重对称性。
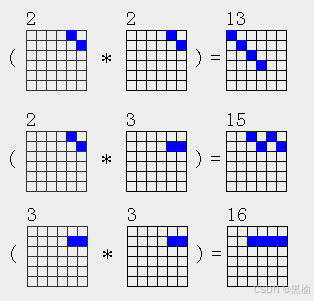
| 2a2*2a2=4a13 |
| 2a2*2a3=4a15 |
| 2a3*2a3=4a16 |
4点结构共有16个,其中只有6个可以被分解为两个结构的积,剩余的10个结构是类质数结构不能被分解。
计算3*2
3ax*2a1
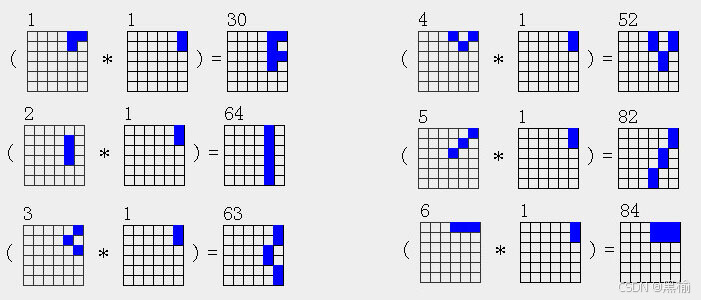
| 3a1*2a1=6a30 |
| 3a2*2a1=6a64 |
| 3a3*2a1=6a63 |
| 3a4*2a1=6a52 |
| 3a5*2a1=6a82 |
| 3a6*2a1=6a84 |
3ax*2a2
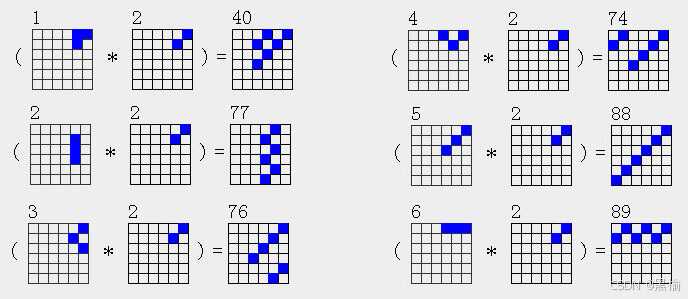
| 3a1*2a2=6a40 |
| 3a2*2a2=6a77 |
| 3a3*2a2=6a76 |
| 3a4*2a2=6a74 |
| 3a5*2a2=6a88 |
| 3a6*2a2=6a89 |
3ax*2a3
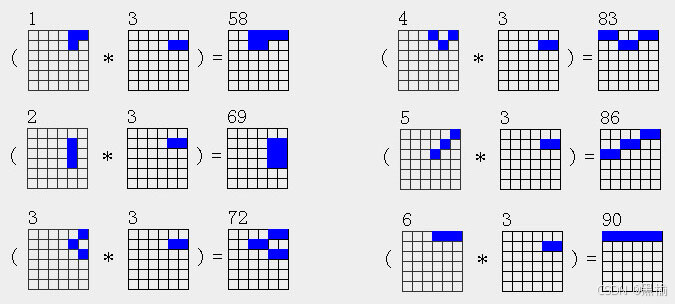
| 3a1*2a3=6a58 |
| 3a2*2a3=6a69 |
| 3a3*2a3=6a72 |
| 3a4*2a3=6a83 |
| 3a5*2a3=6a86 |
| 3a6*2a3=6a90 |
6点结构有90个,只有18个可被分解。
检验结构加法是否有结合律
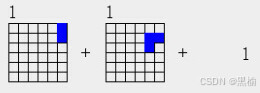
2a1+3a1+1
首先计算2a1+3a1

12(3a1+2a1)=5a1+2*5a3+5a4+5a9+3*5a10+2*5a12+2*5a24
让5a1,3,4,9,10,12,14分别+1

17(5a1+1)=4*5a2+3*5a3+5a4+5a6+5a9+4*5a12+5a15+2*5a30

12(5a3+1)=3*5a1+2*5a6+5a8+2*5a10+2*5a13+5a17+5a32
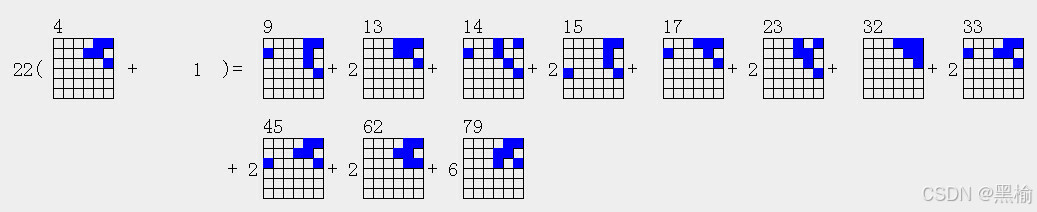
22(5a4+1)=5a9+2*5a13+5a14+2*5a15+5a17+2*5a23+5a32+2*5a33+2*5a45+2*5a62+6*5a79

23(5a9+1)=5a6+2*5a7+5a9+5a15+2*5a23+2*5a25+5a26+2*5a27+3*5a36+2*5a40+4*5a52+2*5a66

12(5a10+1)=5a3+5a22+2*5a28+2*5a30+4*5a31+2*5a42

13(5a12+1)=2*5a12+5a24+2*5a30+5a32+5a62+6*5a69

13(5a24+1)=5a13+5a32+5a41+2*5a58+6*5a84+2*5a85
考虑系数1,2,1,1,3,2,2把结果加起来
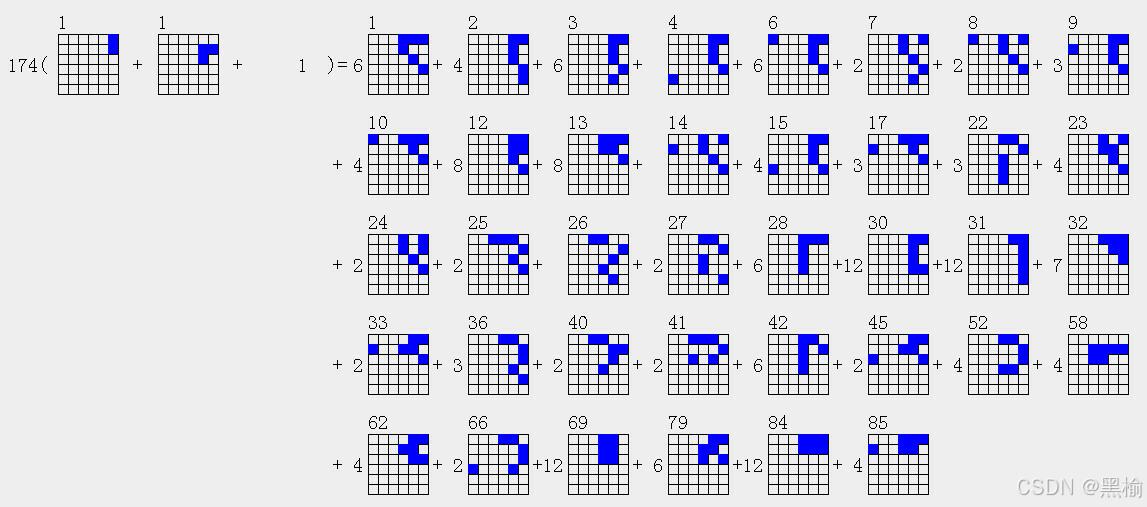
174(2a1+3a1+1)=6*5a1+4*5a2+6*5a3+5a4+6*5a6+2*5a7+2*5a8+3*5a9+4*5a10+8*5a12+8*5a13+5a14+4*5a15+3*5a17+3*5a22+4*5a23+2*5a24+2*5a25+5a26+2*5a27+6*5a28+12*5a30+12*5a31+7*5a32+2*5a33+3*5a36+2*5a40+2*5a41+6*5a42+2*5a45+4*5a52+4*5a58+4*5a62+2*5a66+12*5a69+6*5a79+12*5a84+4*5a85
第二种方法,先计算3a1+1

将4a1,2,3,4,12,14分别加2a1

18(4a1+2a1)=3*6a1+3*6a3+6a7+2*6a13+2*6a23+4*6a30+3*6a79
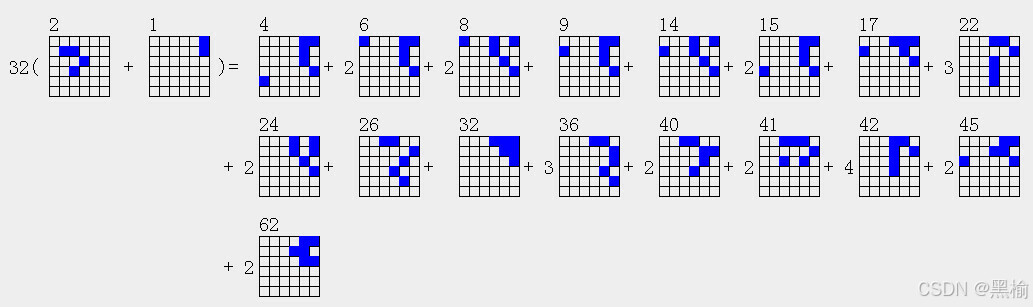
32(4a2+2a1)=6a4+2*6a6+2*6a8+6a9+6a14+2*6a15+6a17+3*6a22+2*6a24+6a26+6a32+3*6a36+2*6a40+2*6a41+4*6a42+2*6a45+2*6a62
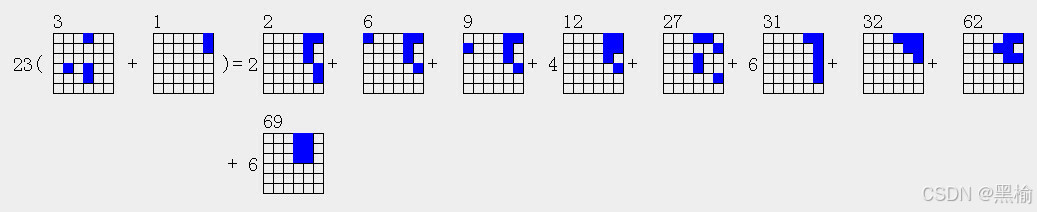
23(4a3+2a1)=2*6a2+6a6+6a9+4*6a12+6a27+6*6a31+6a32+6a62+6*6a69

11(4a4+2a1)=6a6+2*6a10+6a25+3*6a28+6a32+6a33+2*6a58

6(4a12+2a1)=6a13+6a30+6a52+3*6a84

7(4a14+2a1)=6a15+6a17+6a32+6a42+6a66+2*6a85
考虑系数把等式右侧相加和第一种方法得到的结构是一致的。由此至少有理由假设结构加法同样符合结合律。
验算乘法的结合律
计算
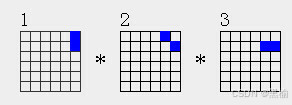
2a1*2a2*2a3

(2a1*2a2)*2a3=4a8*2a3=8a529

2a1*(2a2*2a3)=2a1*4a15=8a529
8a529这个结构有3重对称性。
所以有理由猜测结构乘法同样有结合律。
