单调栈应用介绍
单调栈应用介绍
- 定义
- 应用场景
- 实现模板
- 具体示例
- 下一个最大元素I
- 问题描述
- 问题分析
- 代码实现
- 柱状图中最大的矩形
- 问题描述
- 问题分析
- 代码实现
- 接雨水
- 问题描述
- 问题分析
- 代码实现
- 最大宽度坡
- 问题描述
- 问题分析
- 代码实现
- 132模式
- 问题描述
- 问题分析
- 代码实现
定义
栈(Stack)是另一种操作受限的线性表,只允许元素从栈的顶端进顶端出,具有后进先出(LIFO)的特性。但单调栈(Monotonic Stack)是一种特殊的栈,在满足栈特性的基础上,栈内元素从栈底到栈顶具有单调性。如果栈底到栈顶元素是单调递减,则称为单调递减栈;如果栈底到栈顶元素是单调递增,则称为单调递增栈。
单调栈具有以下特性:
- 新元素加入栈顶时,需要进行单调性维护,弹出不满足单调性的栈顶元素
- 当前解计算是在出栈的时候进行的
应用场景
- 下一个最大元素,对应单调递减栈
- 下一个最小元素,对应单调递增栈
- 上一个最大元素,反向入栈,即从数据尾部往前遍历,对应单调递减栈
- 上一个最小元素,反向入栈,即从数据尾部往前遍历,对应单调递增栈
以上是单调栈最基础的应用场景,很多问题也是对这些场景的变种,我们需要一针见血的直指问题核心。
实现模板
在代码实现上,主要涉及两个动作(动作之间的顺序需要根据具体问题场景灵活调整):
- 维护栈顶: 保证整个栈的单调性,新元素入栈时,及时弹出栈顶不满足单调性的元素
- 问题解计算逻辑:在弹出栈顶时,计算问题解
伪代码如下:
ans = 问题初始解
//tips:由于下面流程必须判断栈非空,某些场景下,可以构造一个不影响结果又能保证栈永远非空的初始化栈,这样就避免判断栈非空逻辑 ---
stack<栈内元素类型> stk = 初始化栈;
//正常处理流程
for(const auto& item: dataSource){while (!stk.empty() && checkMonotonic(stk.top(), item)) {//计算问题解ans = 问题解计算逻辑stk.pop();}stk.push(x);
}//在某些场景下,需要保证所有元素出栈 --- 可以通过一些辅助数据来 保证所有数据在上面流程中全部出栈,这样可以省略以下逻辑,保证代码简洁性
while (!stk.empty()) {//计算问题解ans = 问题解计算逻辑stk.pop();
}
单调栈的结构简单,应用形式灵活,需要结合具体问题灵活处理。
具体示例
下一个最大元素I
496. 下一个更大元素 I
问题描述
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 4 ,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
- 1 ,nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
示例 2:
输入:nums1 = [2,4], nums2 = [1,2,3,4].
输出:[3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 2 ,nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。
问题分析
本题的问题描述看着挺复杂的,但由于nums1是nums2的子集,即nums1中的数值都在nums2中,且无重复数字,所以,这里的问题可以简化先为求nums2中每个元素的下一个最大元素,然后再取nums1中特定元素对应的下一个最大元素。
代码实现
class Solution {
public:vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {//适用hash map存储每个元素对应的下一个最大元素值unordered_map<int,int> preData;stack<int> stk;//使用单调递减栈求取每个元素的下一个最大元素for(int idx = nums2.size() - 1; idx >= 0; --idx){while(!stk.empty() && nums2[idx] >= stk.top()){stk.pop();}preData[nums2[idx]] = stk.empty() ? -1 : stk.top();stk.push(nums2[idx]);}vector<int> ans;//遍历每个元素取值for(int num: nums1){ans.push_back(preData[num]);}return ans;}
};
柱状图中最大的矩形
84. 柱状图中最大的矩形
问题描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
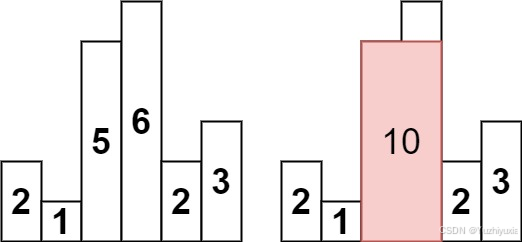
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
示例 2:

输入: heights = [2,4]
输出: 4
问题分析
矩形面积的计算公式为 矩形面积 = 宽 ∗ 高 矩形面积= 宽 * 高 矩形面积=宽∗高,求最大面积需要遍历所有柱子,以该柱子为高的所有矩形面积中的最大面积。当计算某根柱子为高的矩形面积时,只需要确定宽度,即确定矩形的左右边界:
- 左边界:该柱子往左找到第一个比他矮的柱子
- 右边界:该柱子往右找到第一个比他矮的柱子

对应的代码实现如下:
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int ans = 0;int size = heights.size();for(int idx = 0; idx < size; ++idx){//查找左边界:往左找第一个比他矮的柱子int left = idx;while(left > 0 && heights[left - 1] >= heights[idx]) left--;//查找右边界:往右找第一个比他矮的柱子int right = idx;while(right < size - 1 && heights[right + 1] >= heights[idx]) right++;ans = max(ans, heights[idx] * (right - left + 1));}return ans;}
};
这道题作为难度级别为Hard的题目,该实现提交后肯定会超时,超时的原因就是在确定左右边界时会做大量的来回比较,如果我们能够快速找到左右边界,那就ok了。在确定左右边界时,需要找到第一个比他矮的柱子,这不这是单调队列的经典应用场景吗?
对于该问题,需要往左和往右两个方向利用单调递增栈求其第一个比他矮的柱子。
代码实现
先利用单调递增栈分别求出当前柱子的左右边界,然后再计算所有柱子对应的矩形面积,最后取其中最大的矩形面积。
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int size = heights.size();stack<int> stk;//左边界vector<int> left(size,0);for(int idx = 0; idx < size; ++idx){while(!stk.empty() && heights[stk.top()] >= heights[idx]) stk.pop();left[idx] = stk.empty() ? -1 : stk.top();stk.push(idx);}stk = stack<int>();//右边界vector<int> right(size,0);for