二叉树的学习
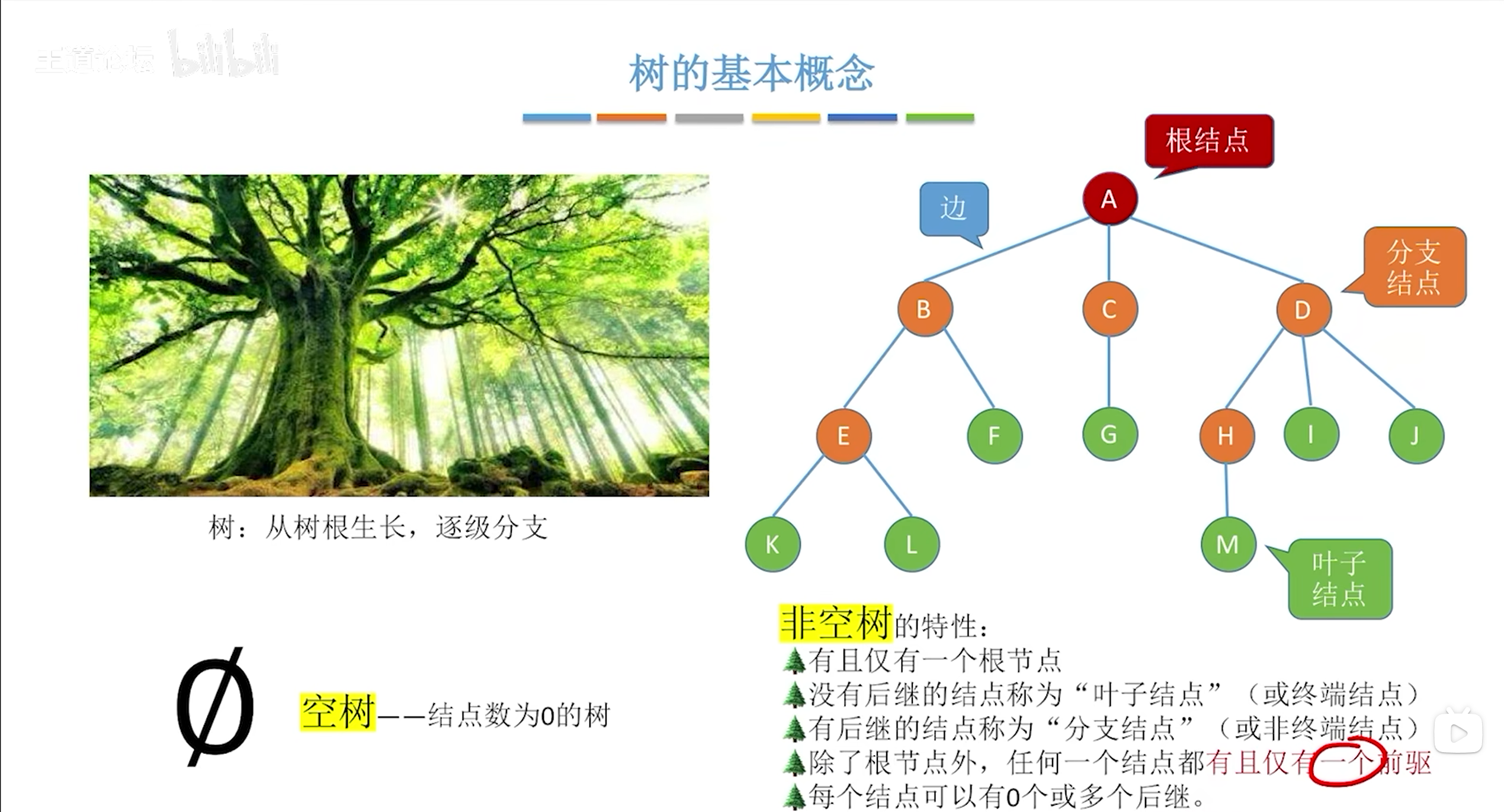
除了根节点外的其他节点只有一个直接前驱,有多个直接前驱的逻辑结构叫做图
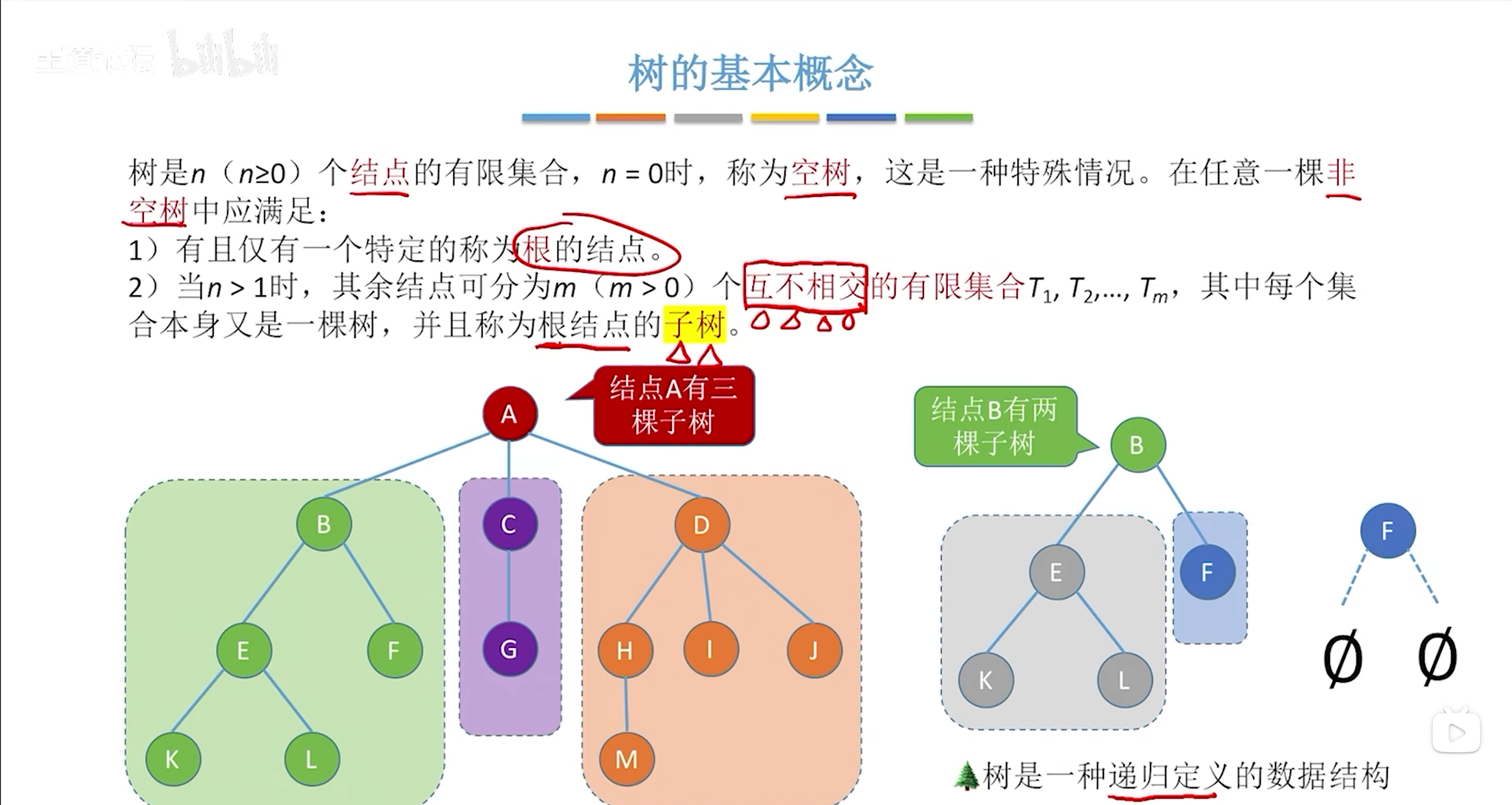
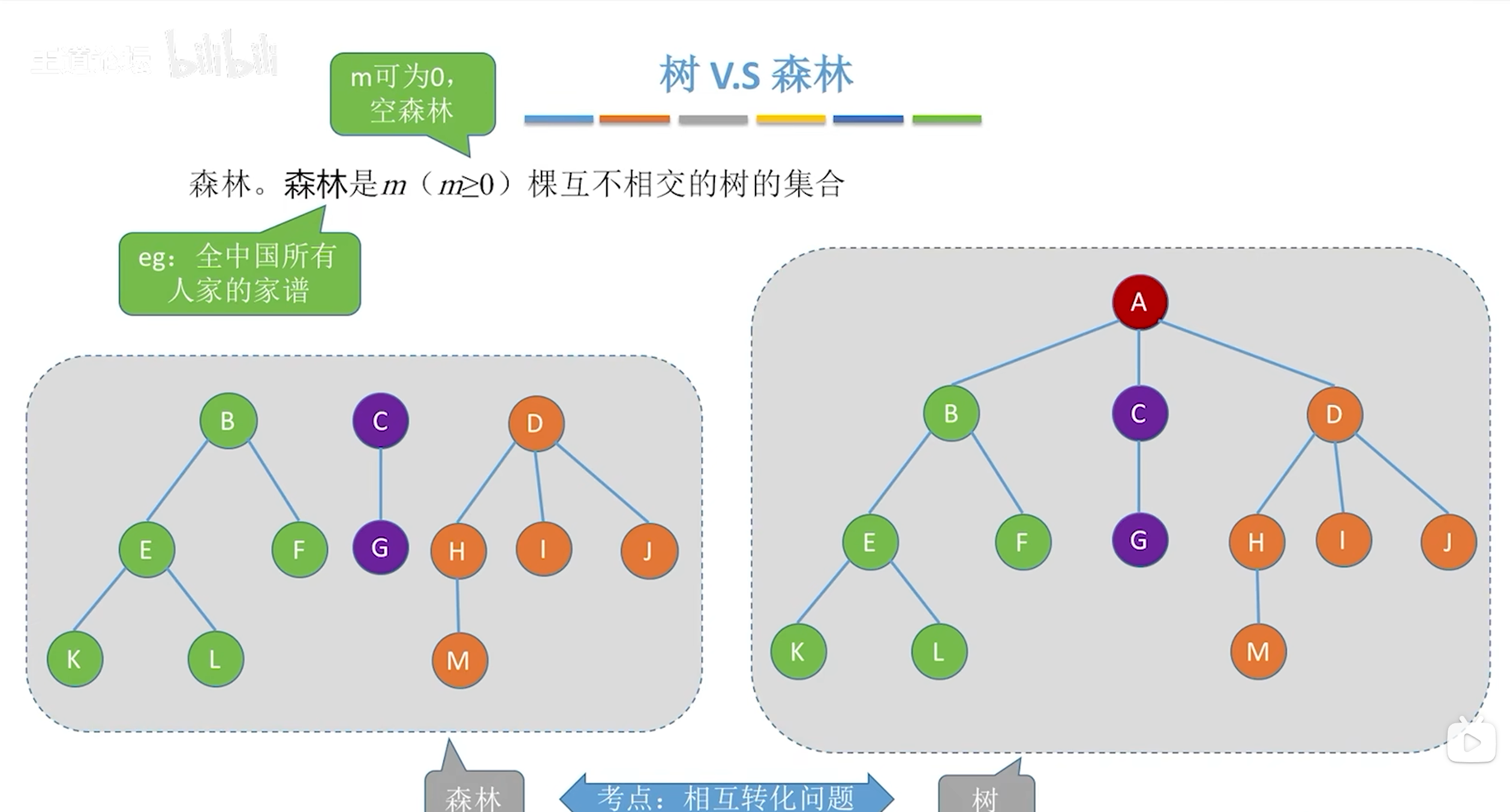
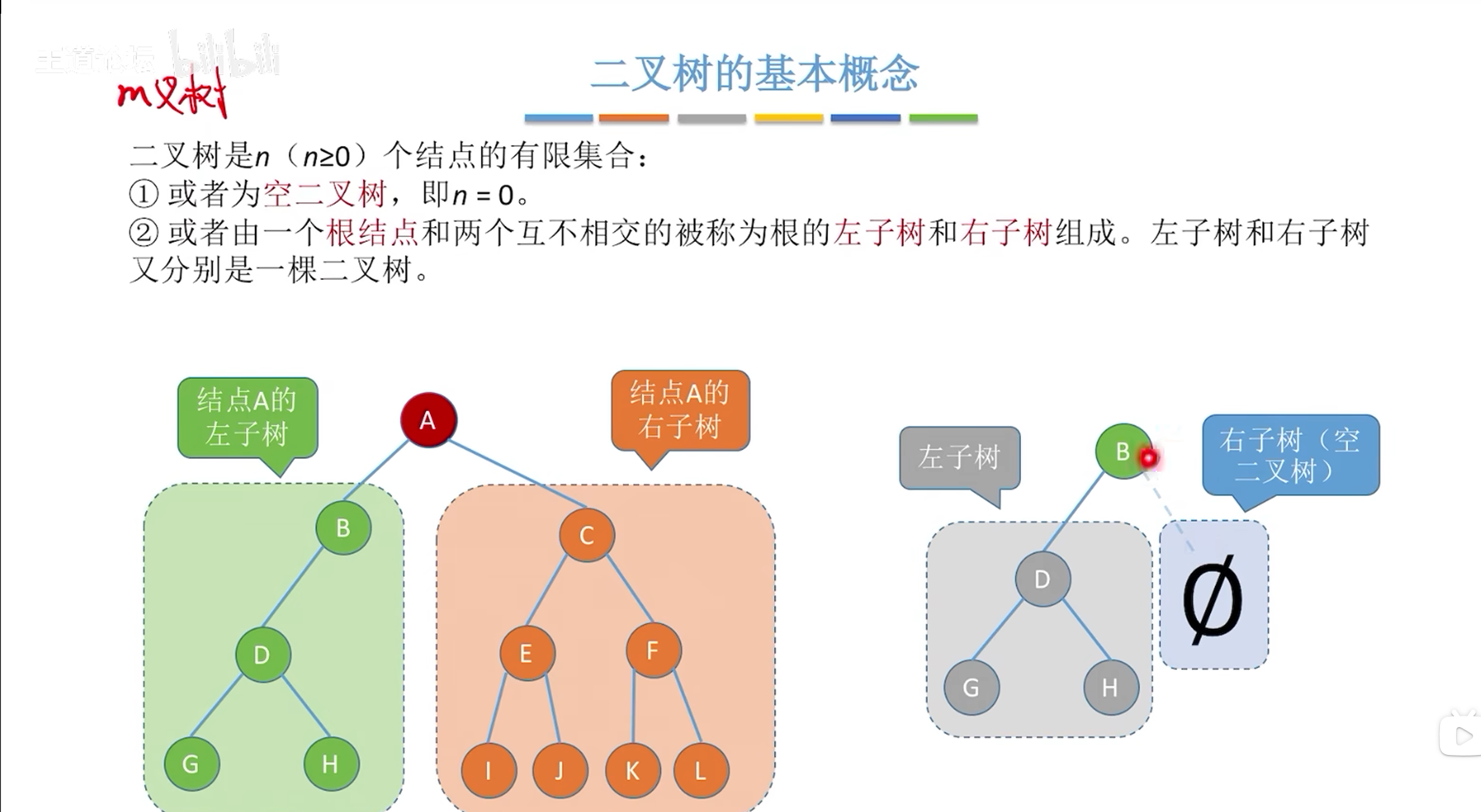
任何一个树都可以看成是一个根节点和若干个不相交的子树构成的;
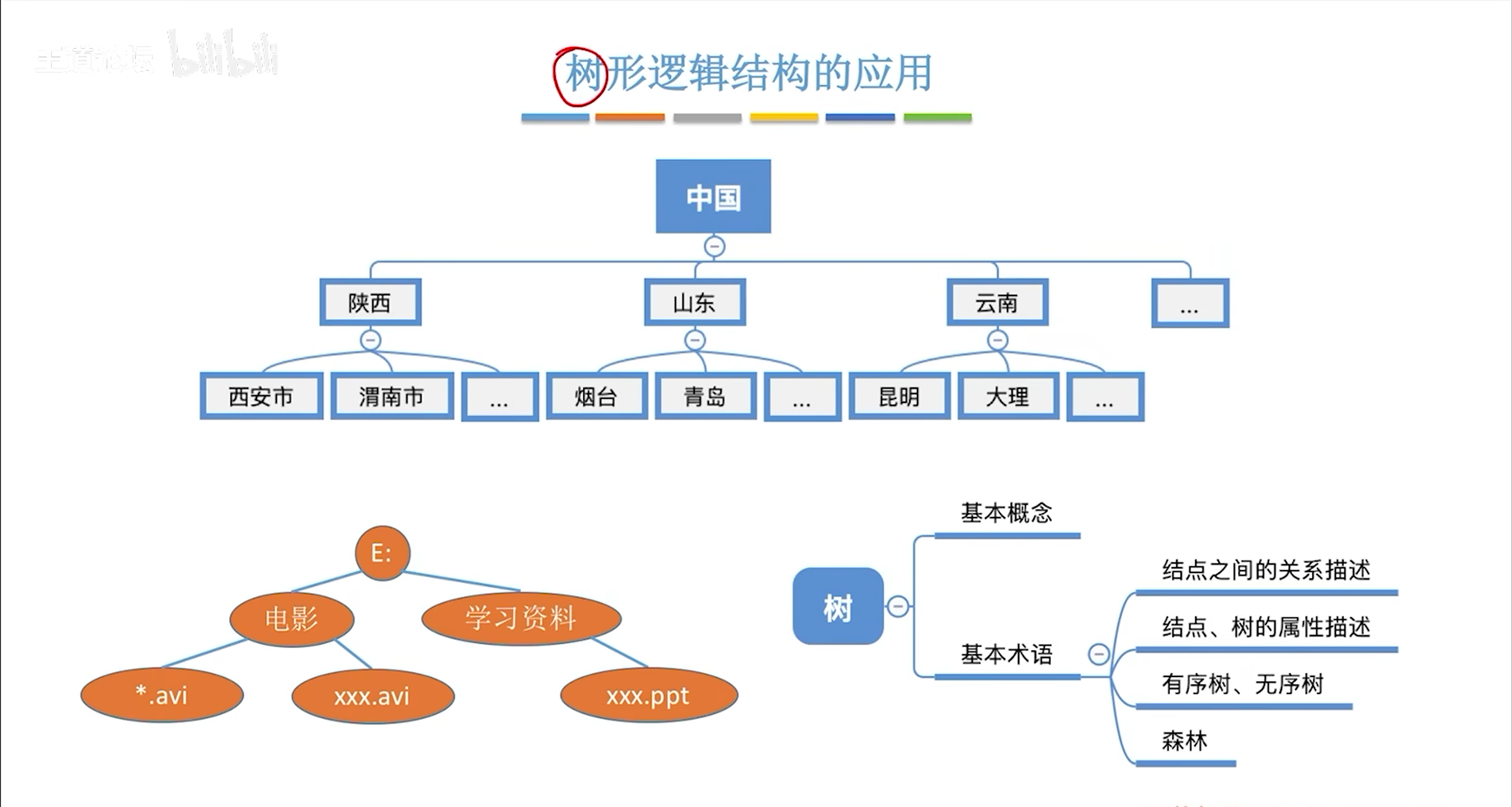
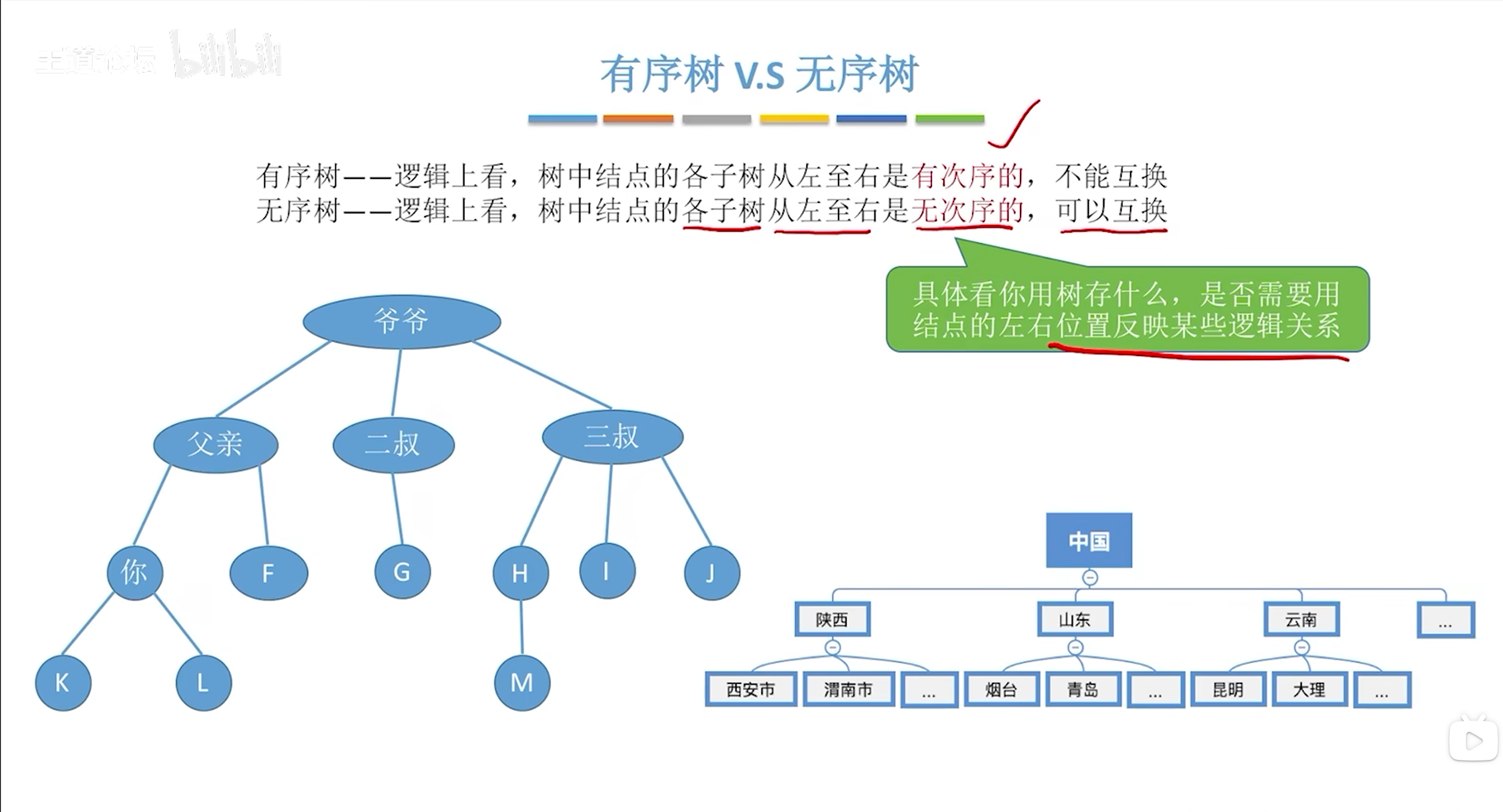
构建思维导图时使用树形结构
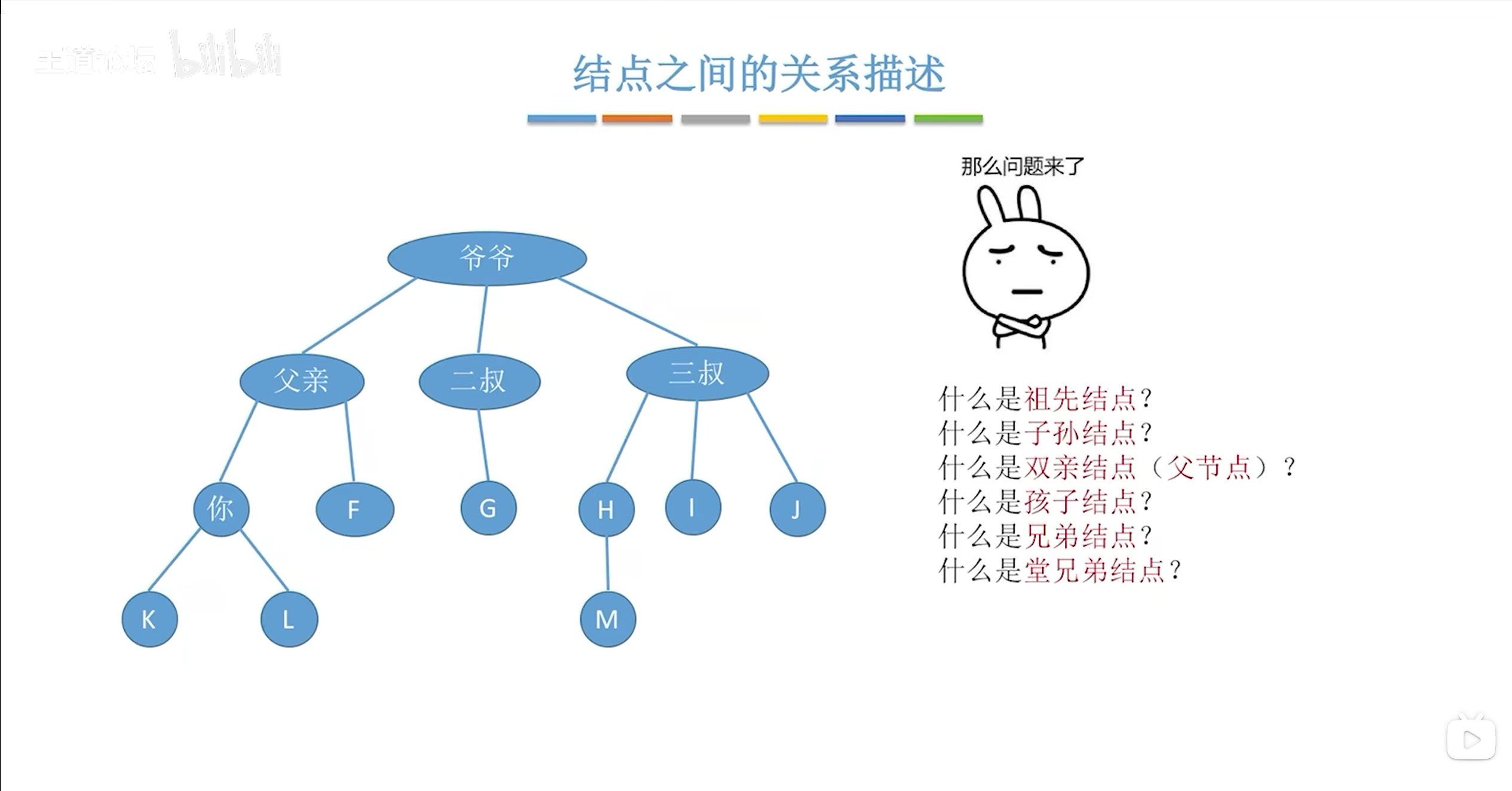
题目中给出AB是堂兄弟节点说明他们处在同一层
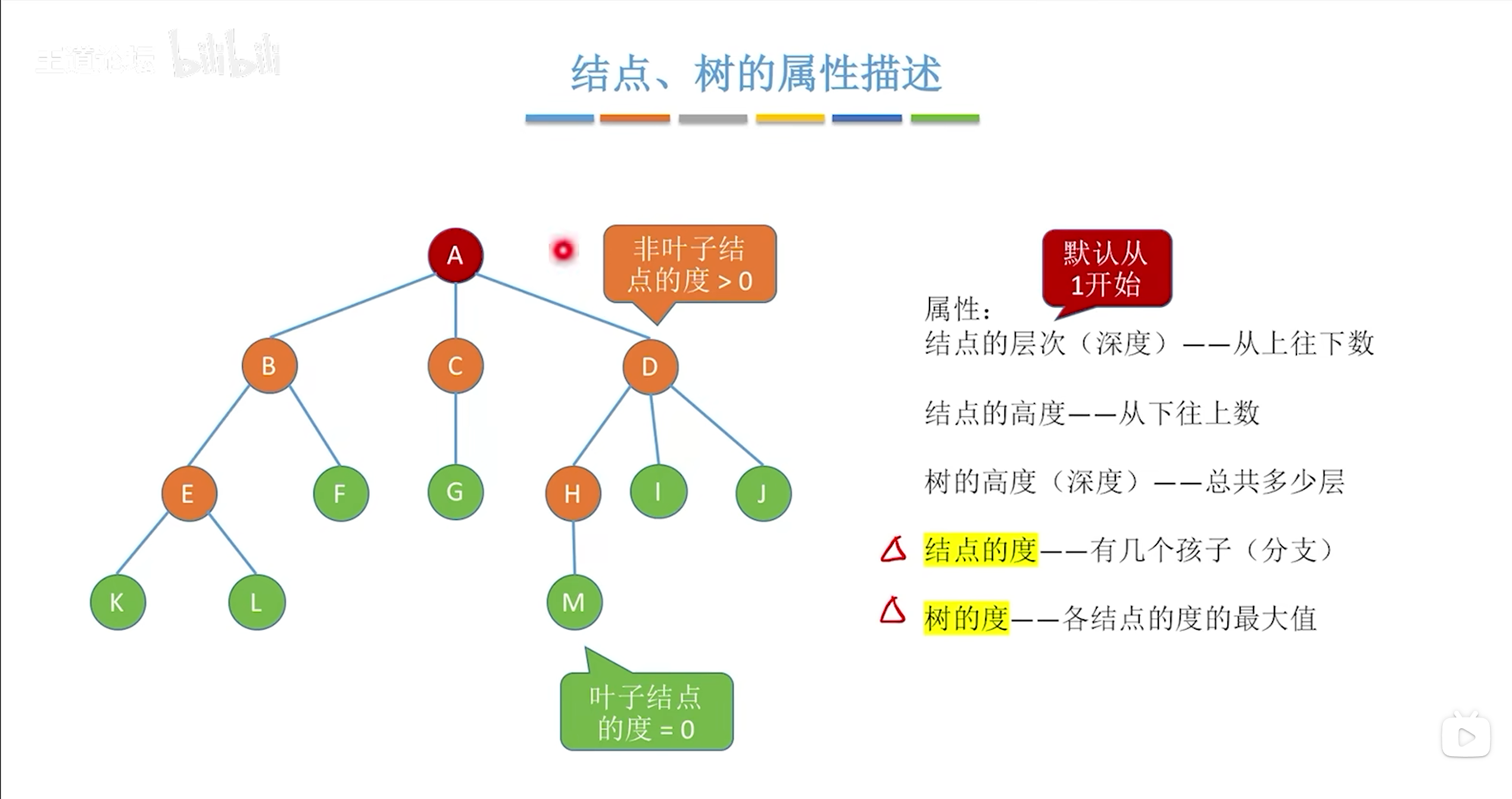
描述两节点之间的路径是从上到下的,同层没有路径,一条边记录长度为1
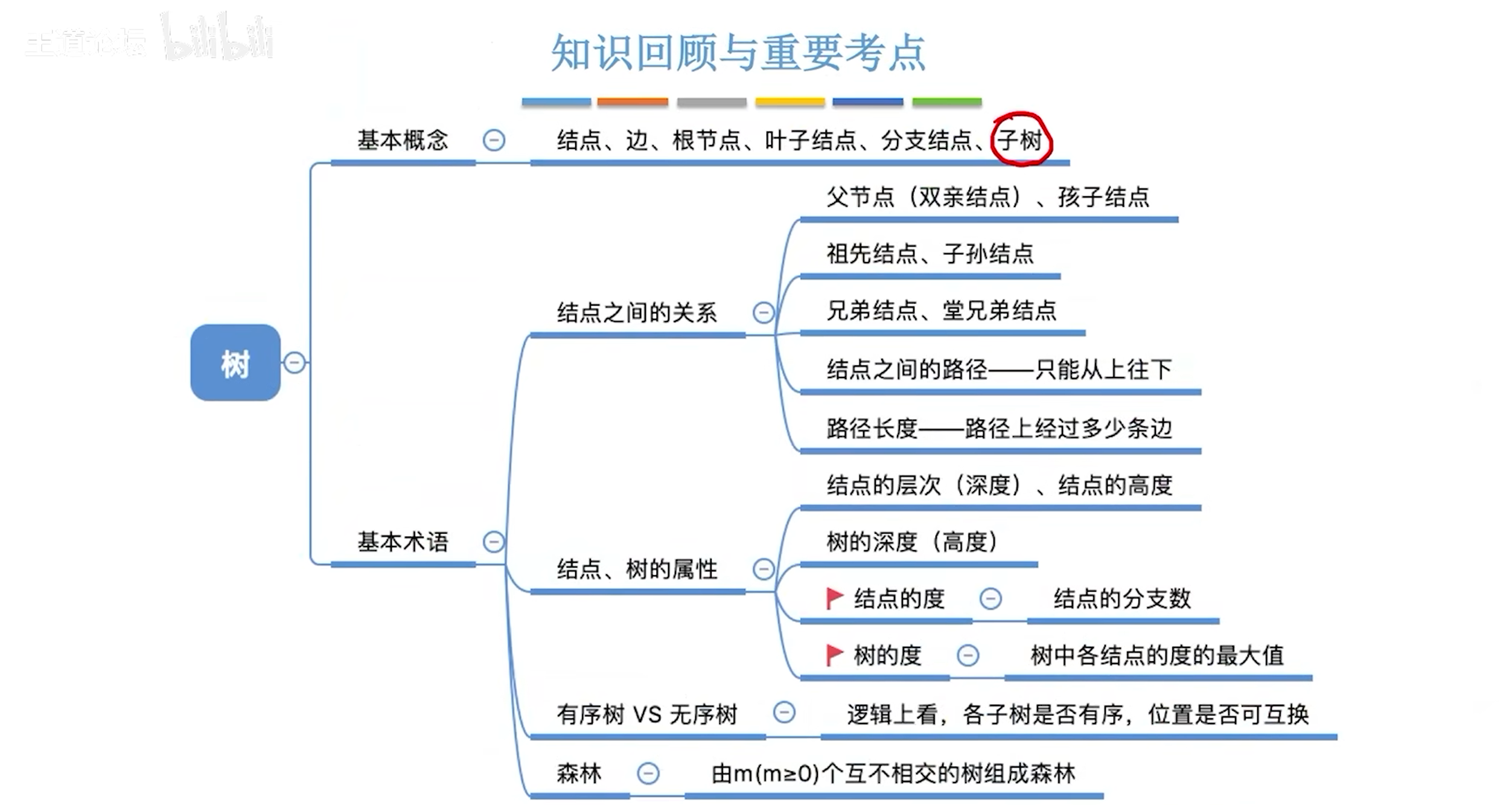
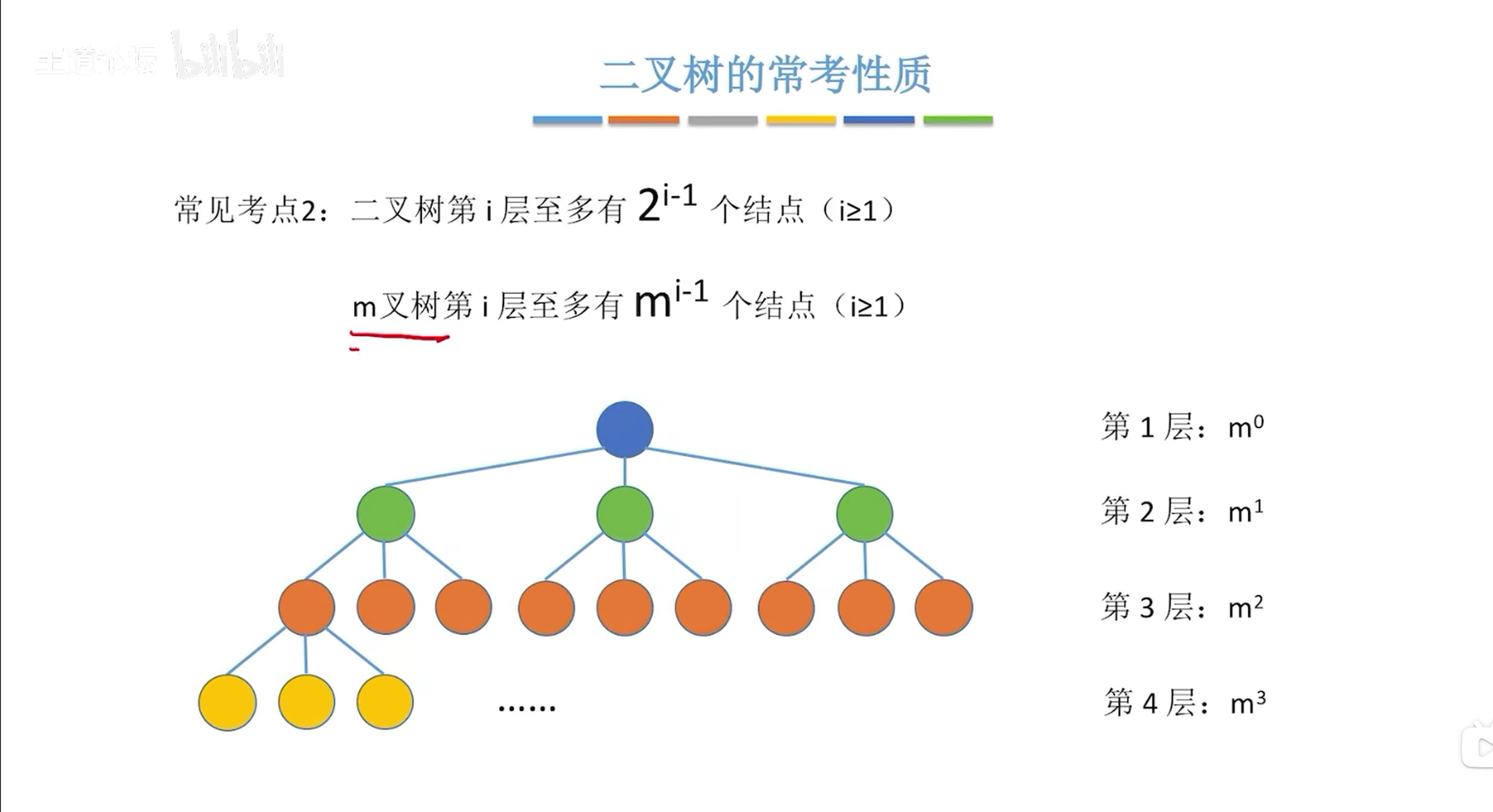
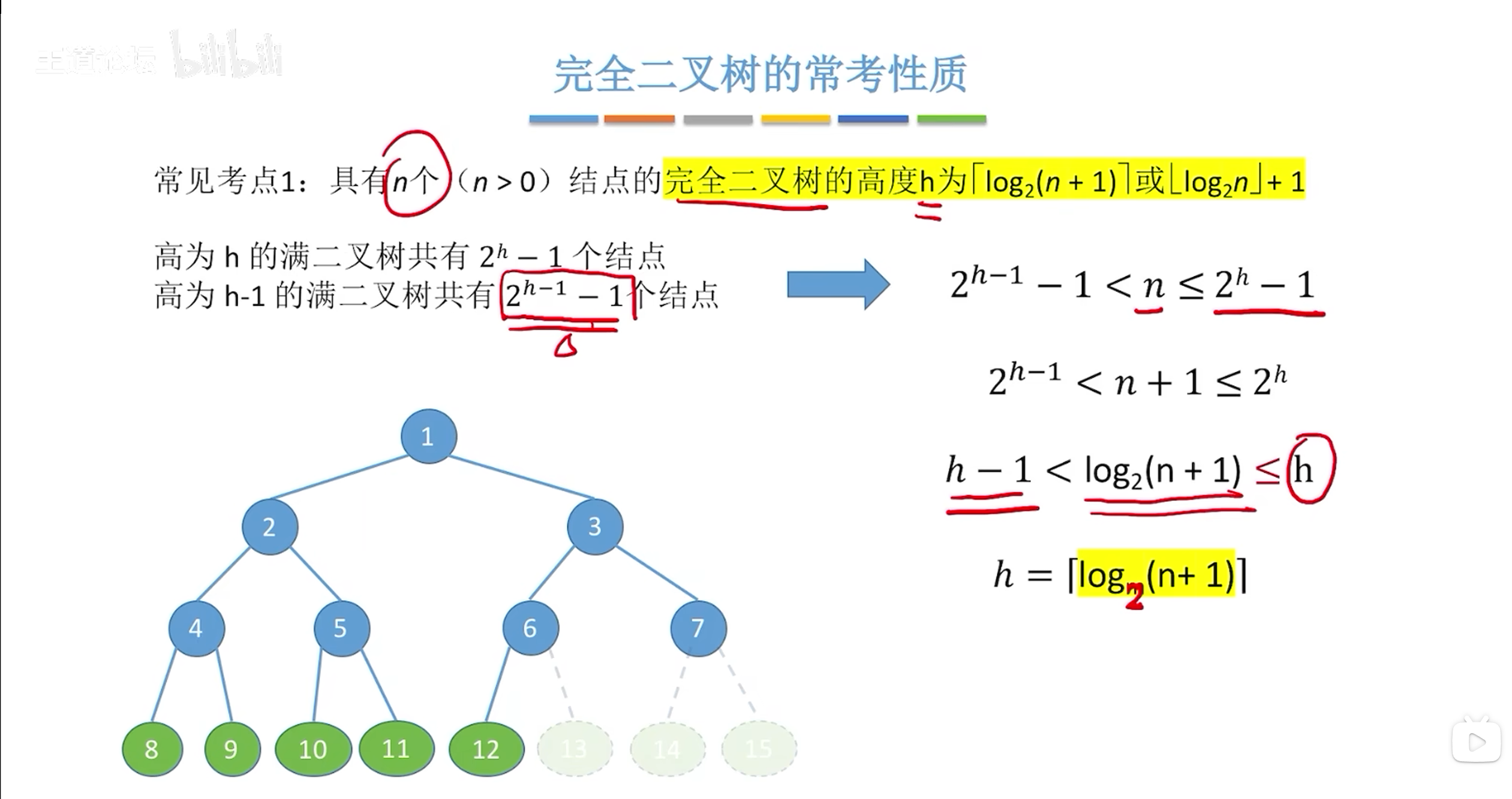
常见考点
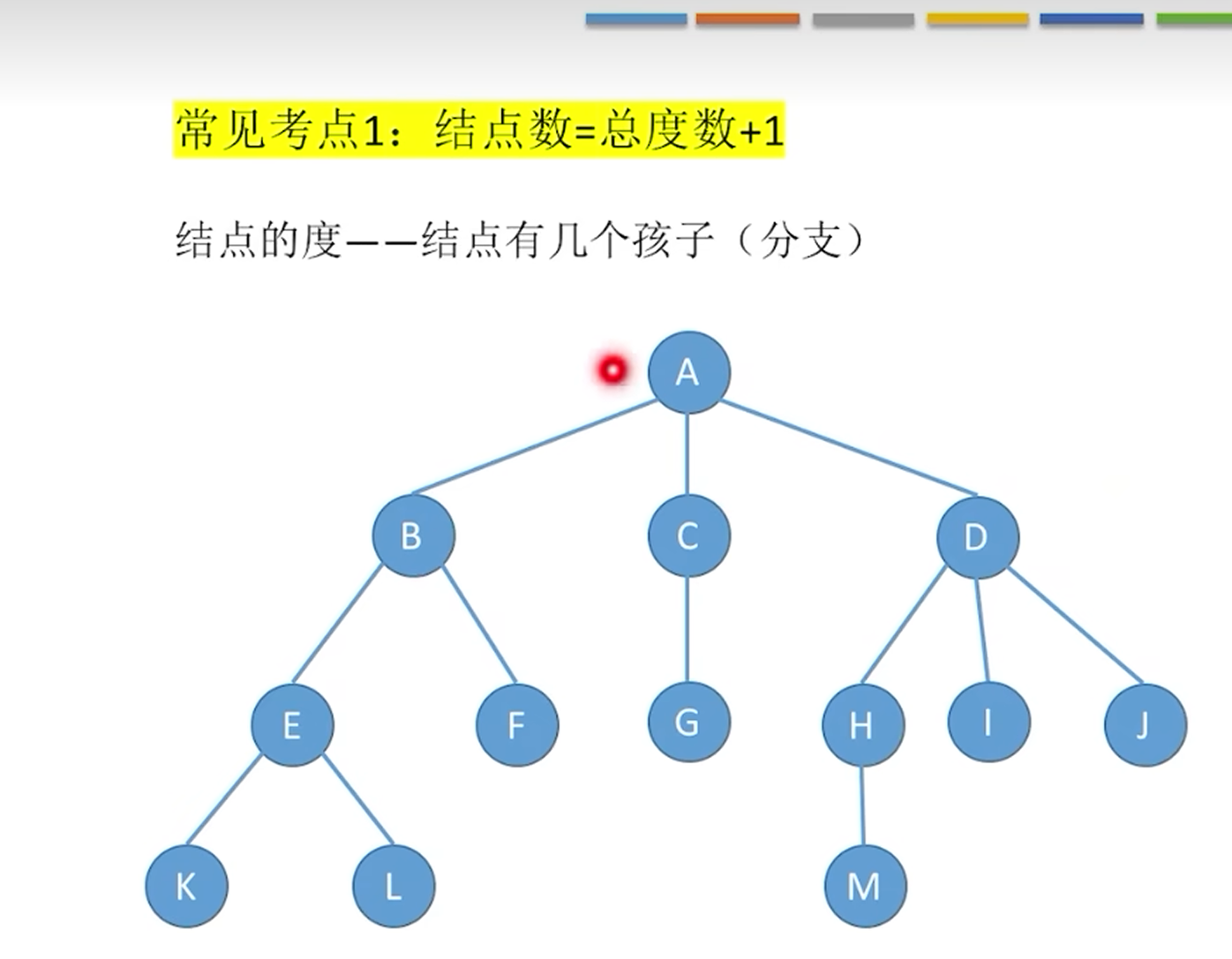
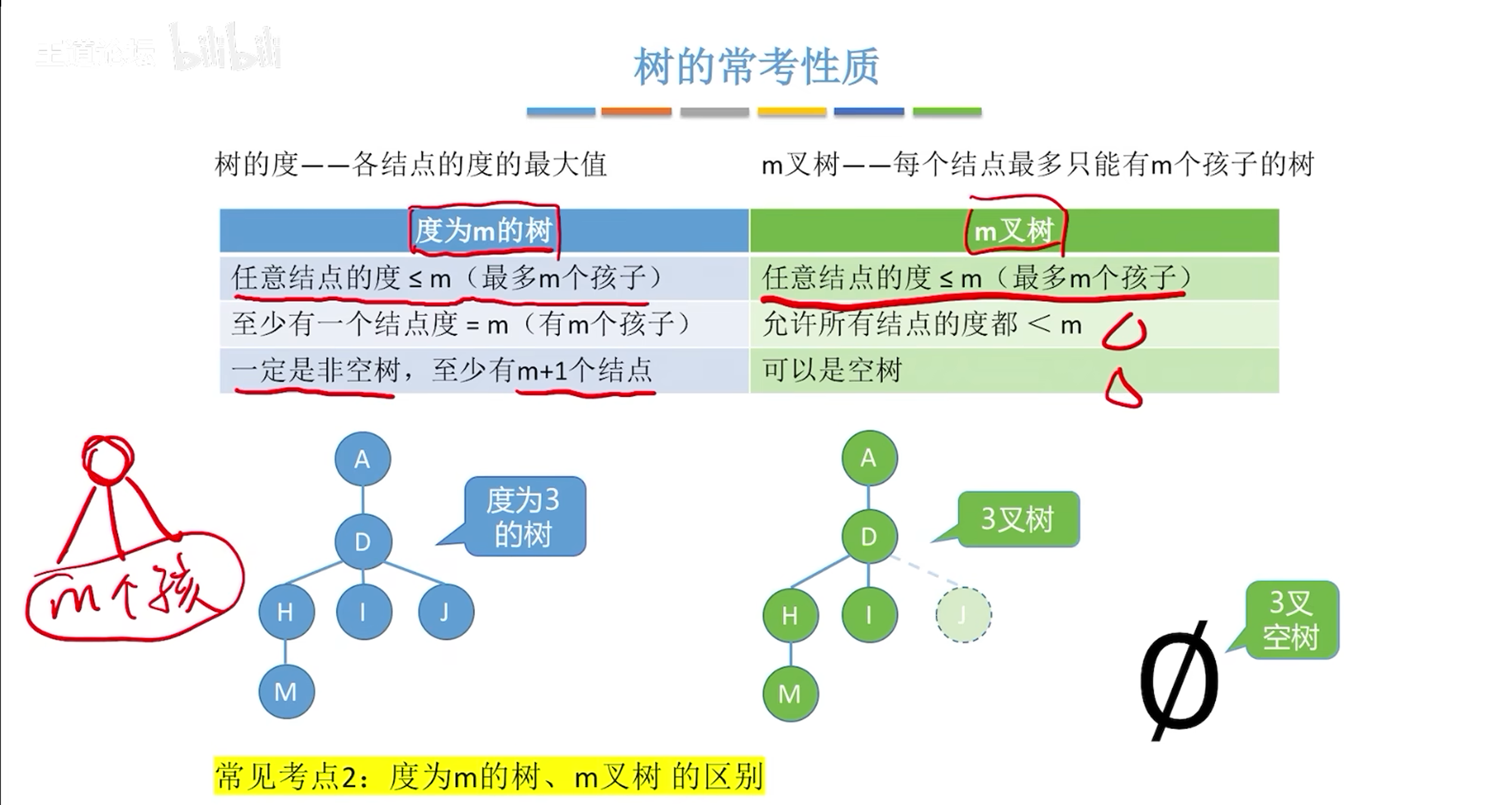
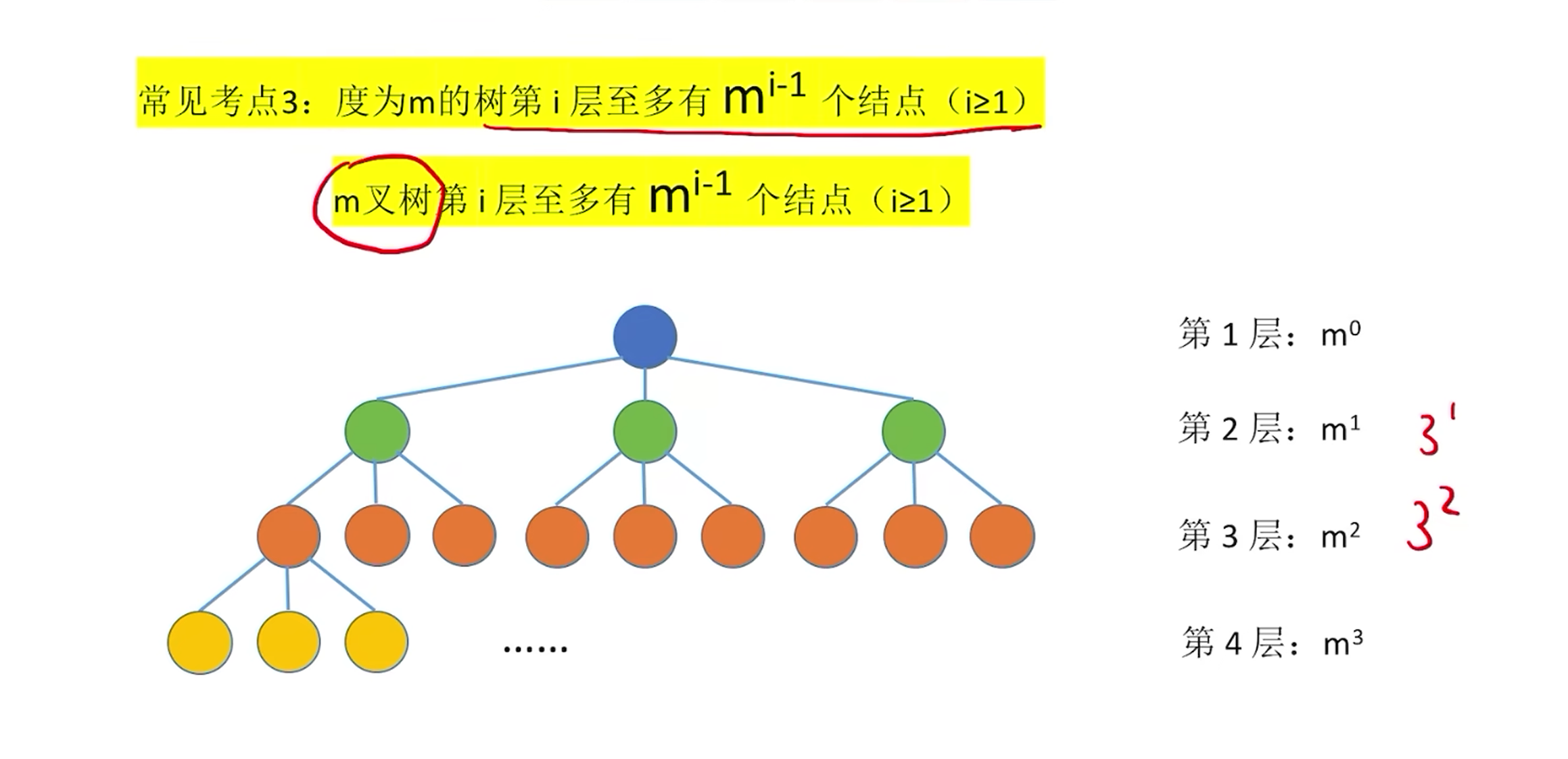
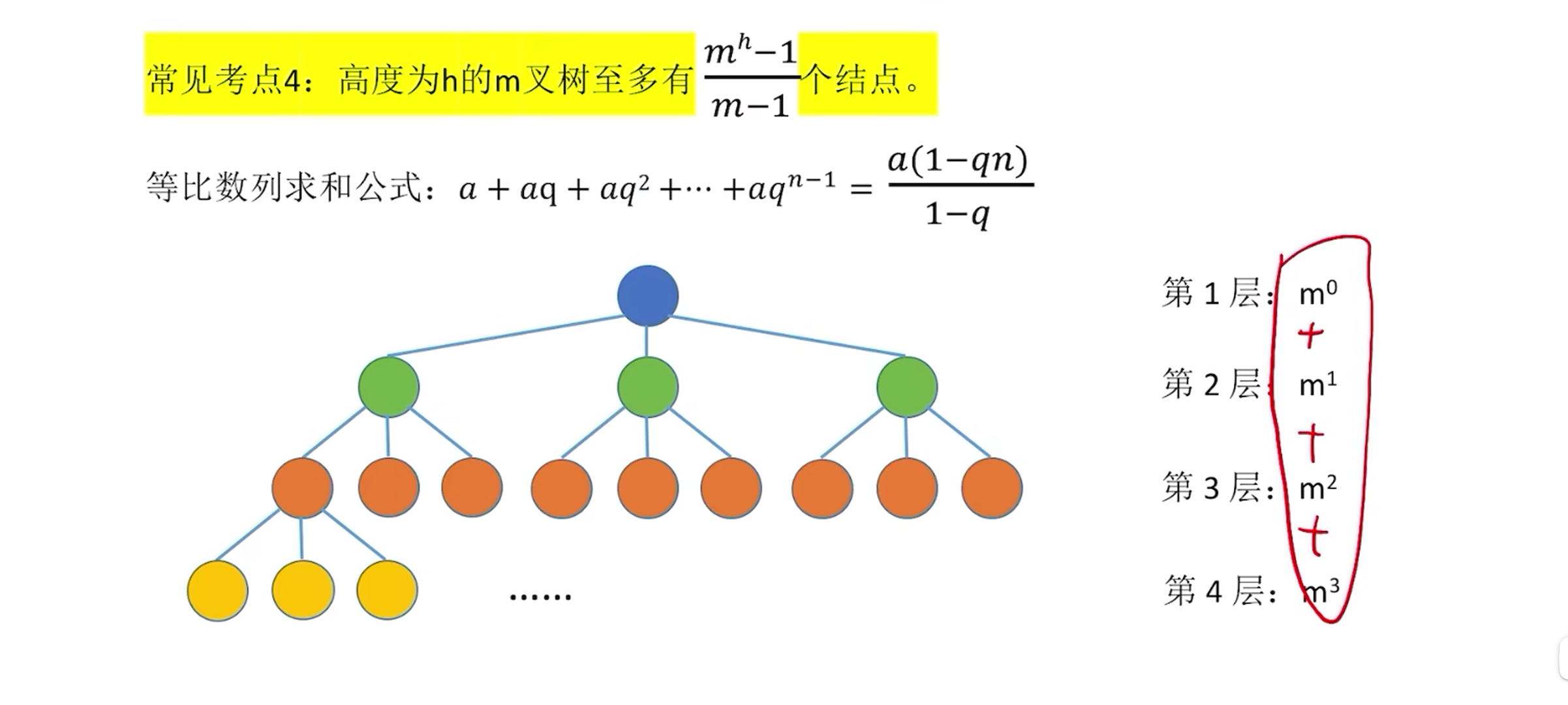


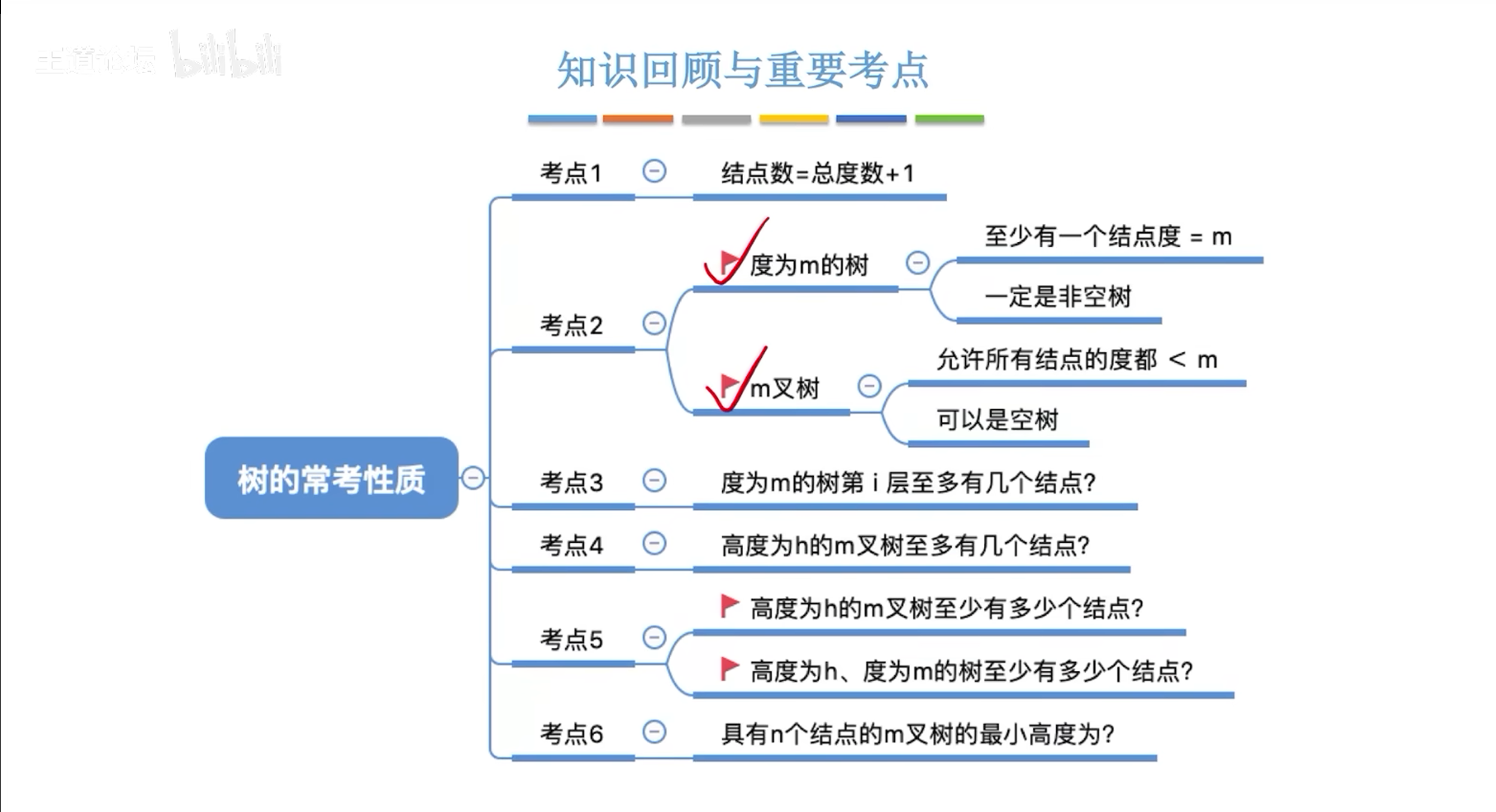
二叉树的详解
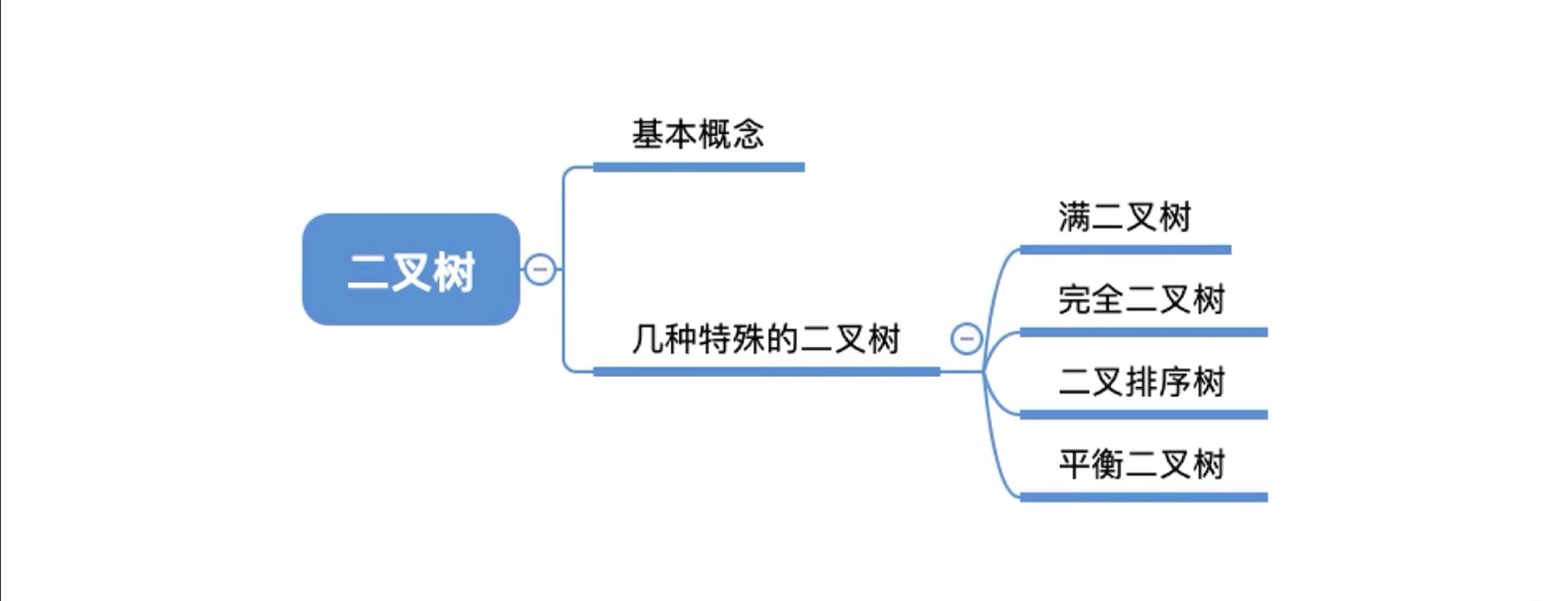
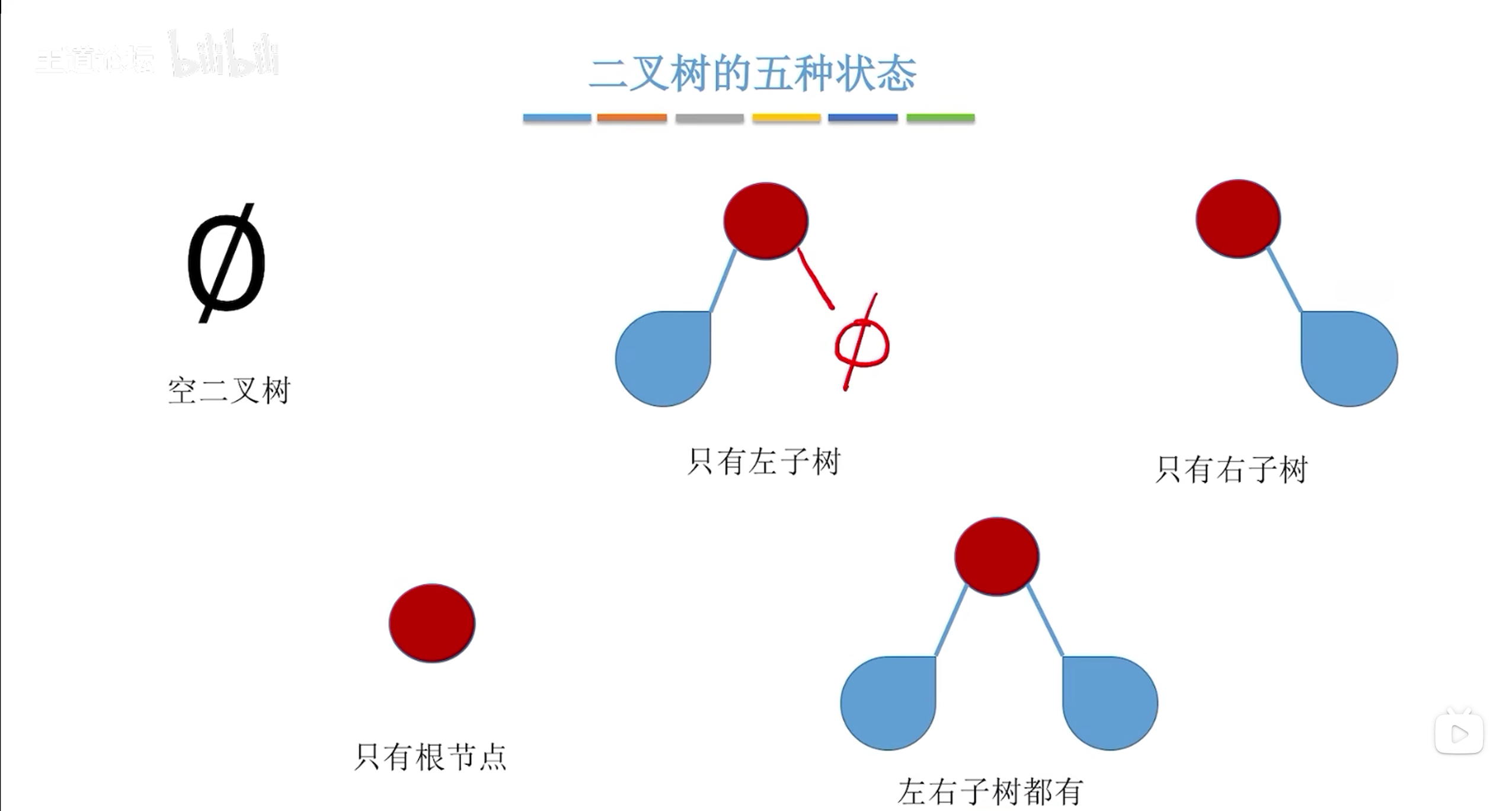

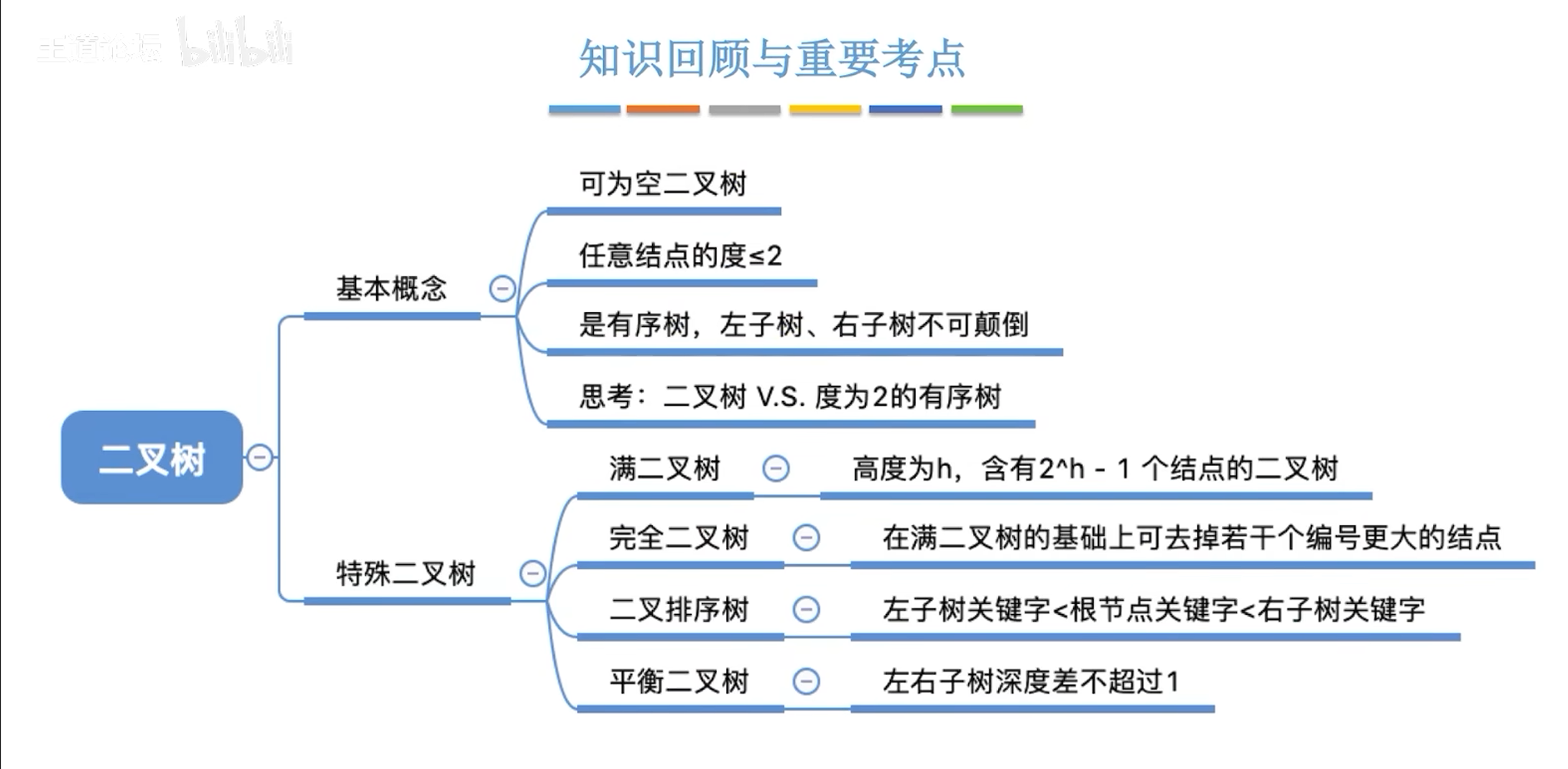
将满二叉树编号更大的节点去掉就是完全二叉树;
满二叉树是一种特殊的完全二叉树;
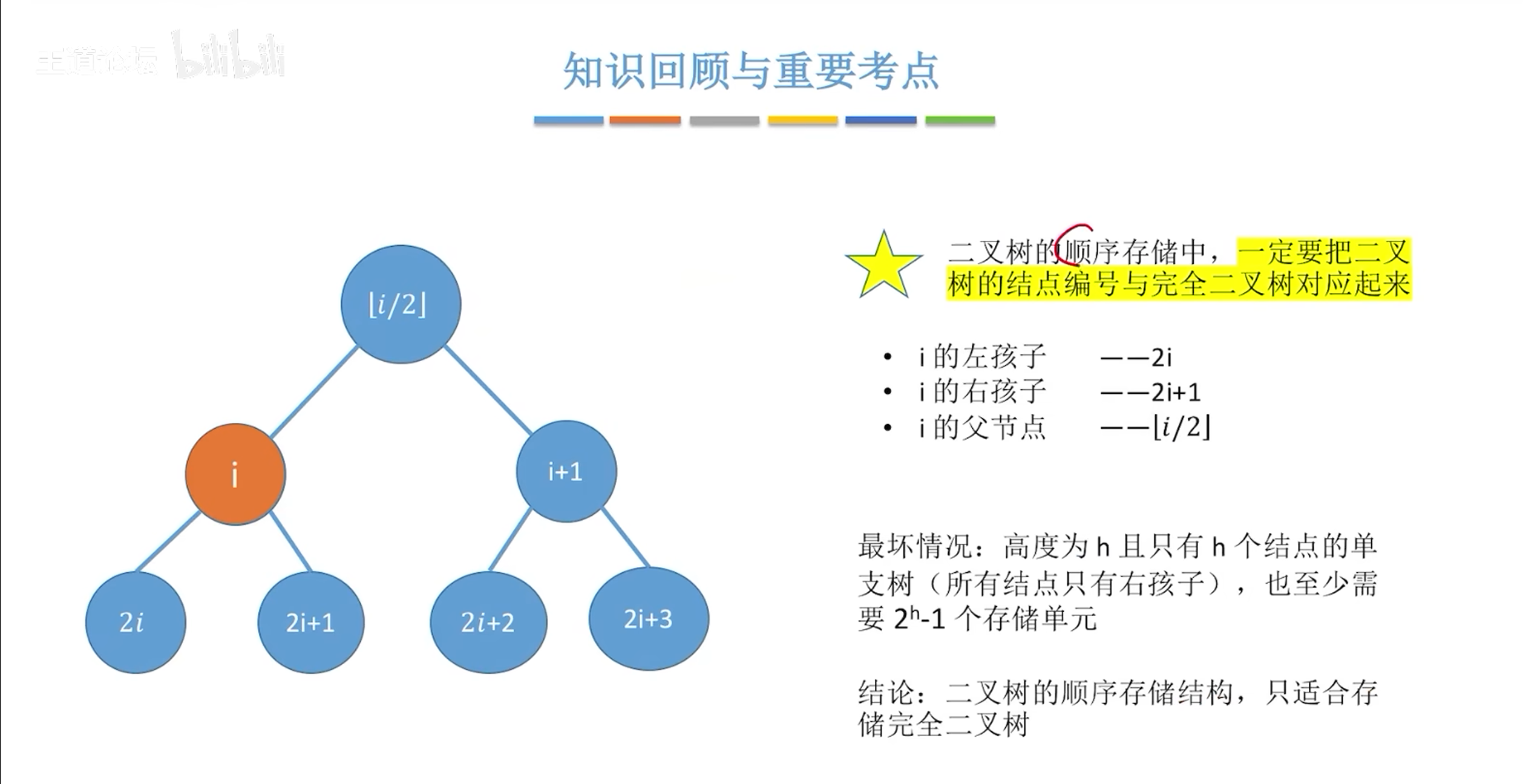
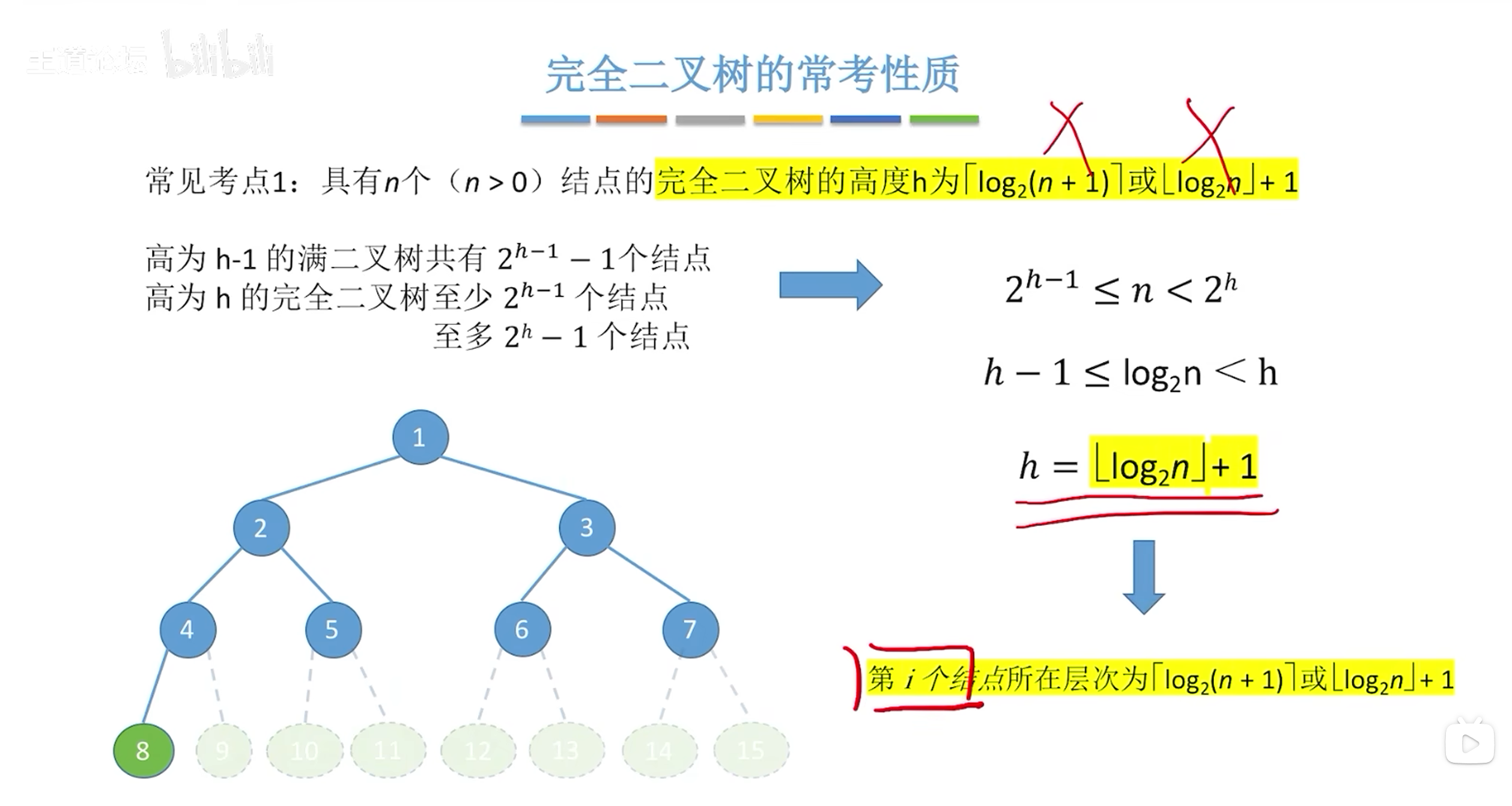
i/2,n/2均为向下取整;i表示当前节点编号,n表示节点总数;
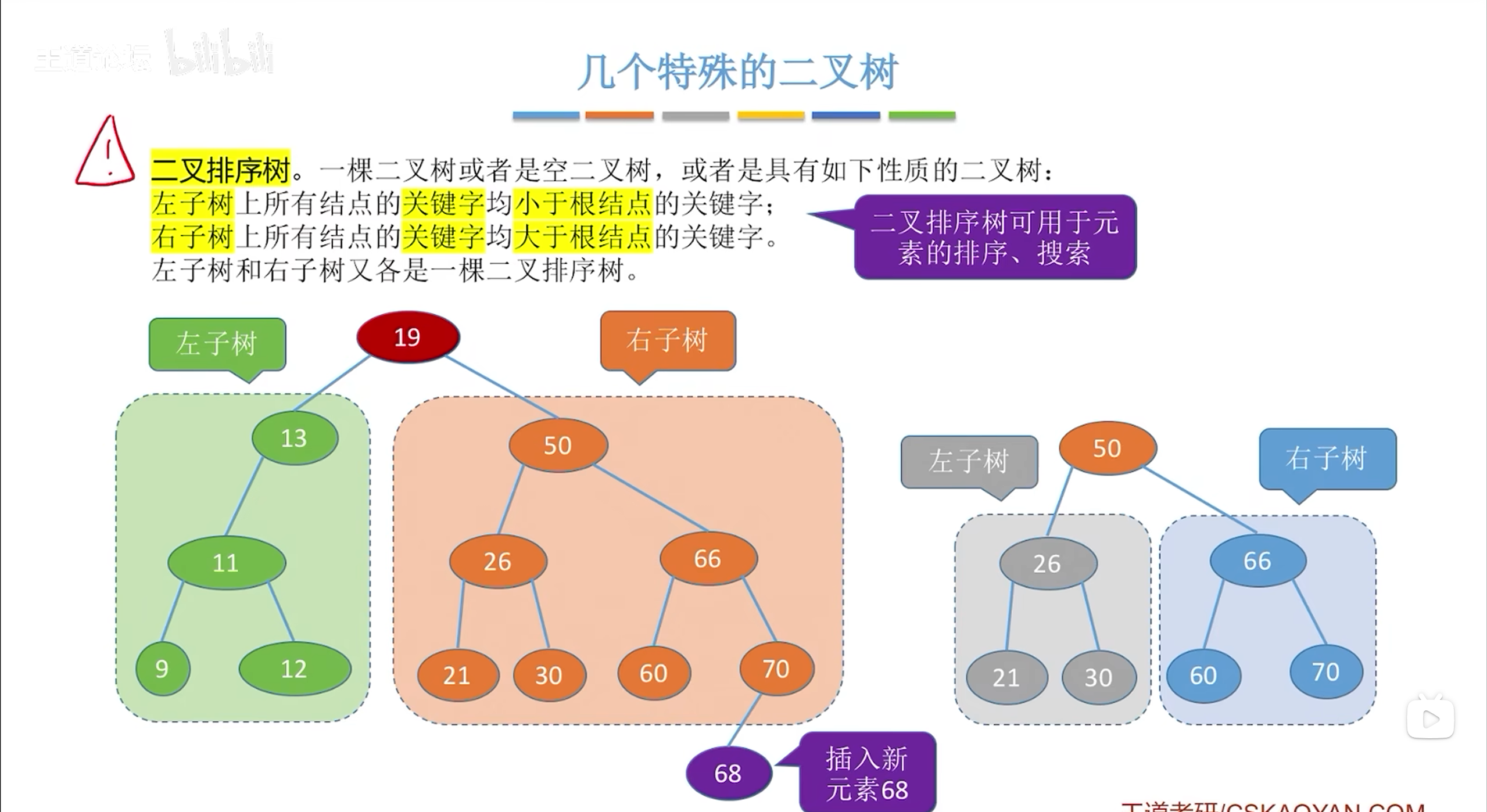
需要经常用到元素的排序搜索时可以使用二叉排序树;
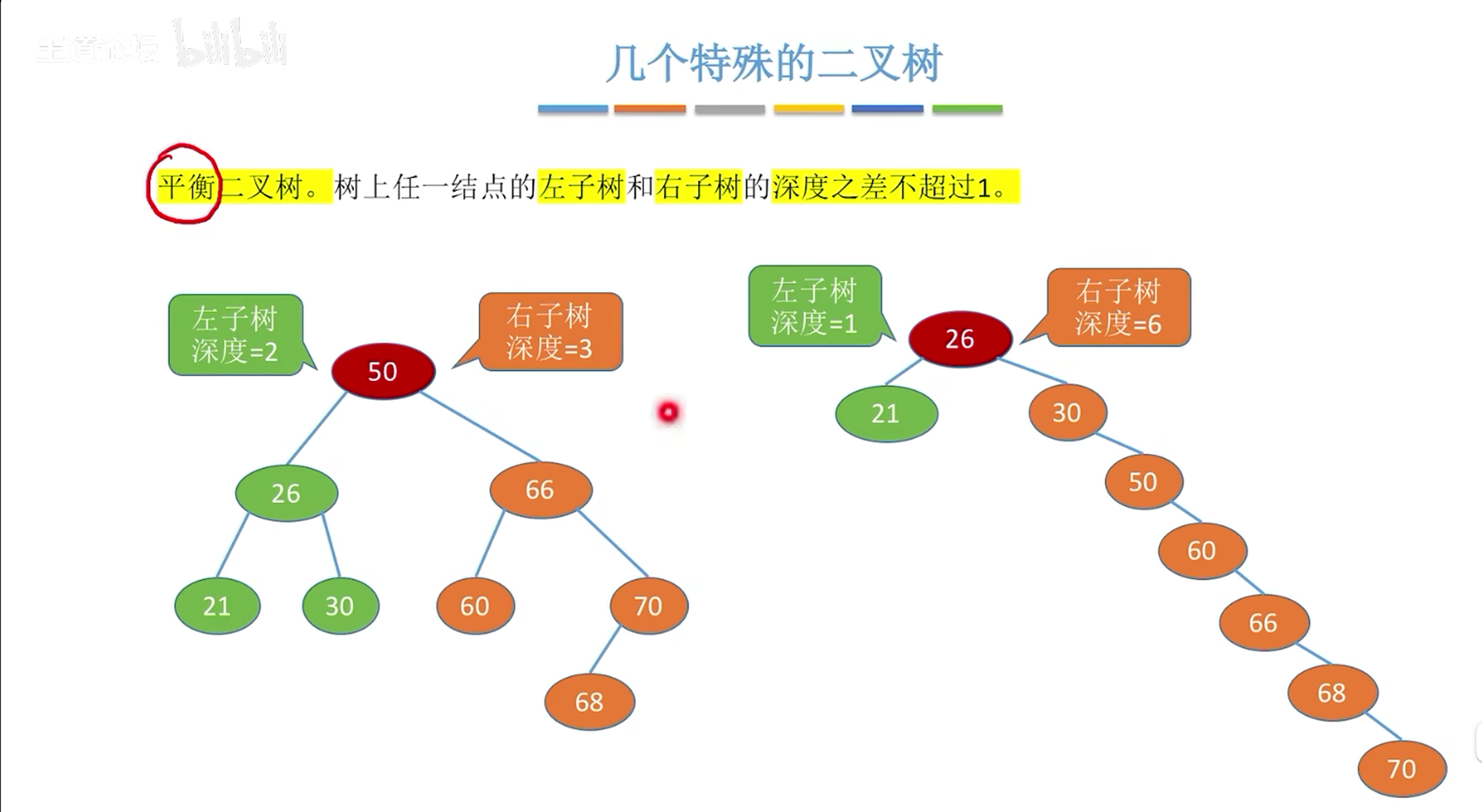
我们追求左右子树的平衡就可以的得到更好更高效的二叉排序树
搜索效率的提升
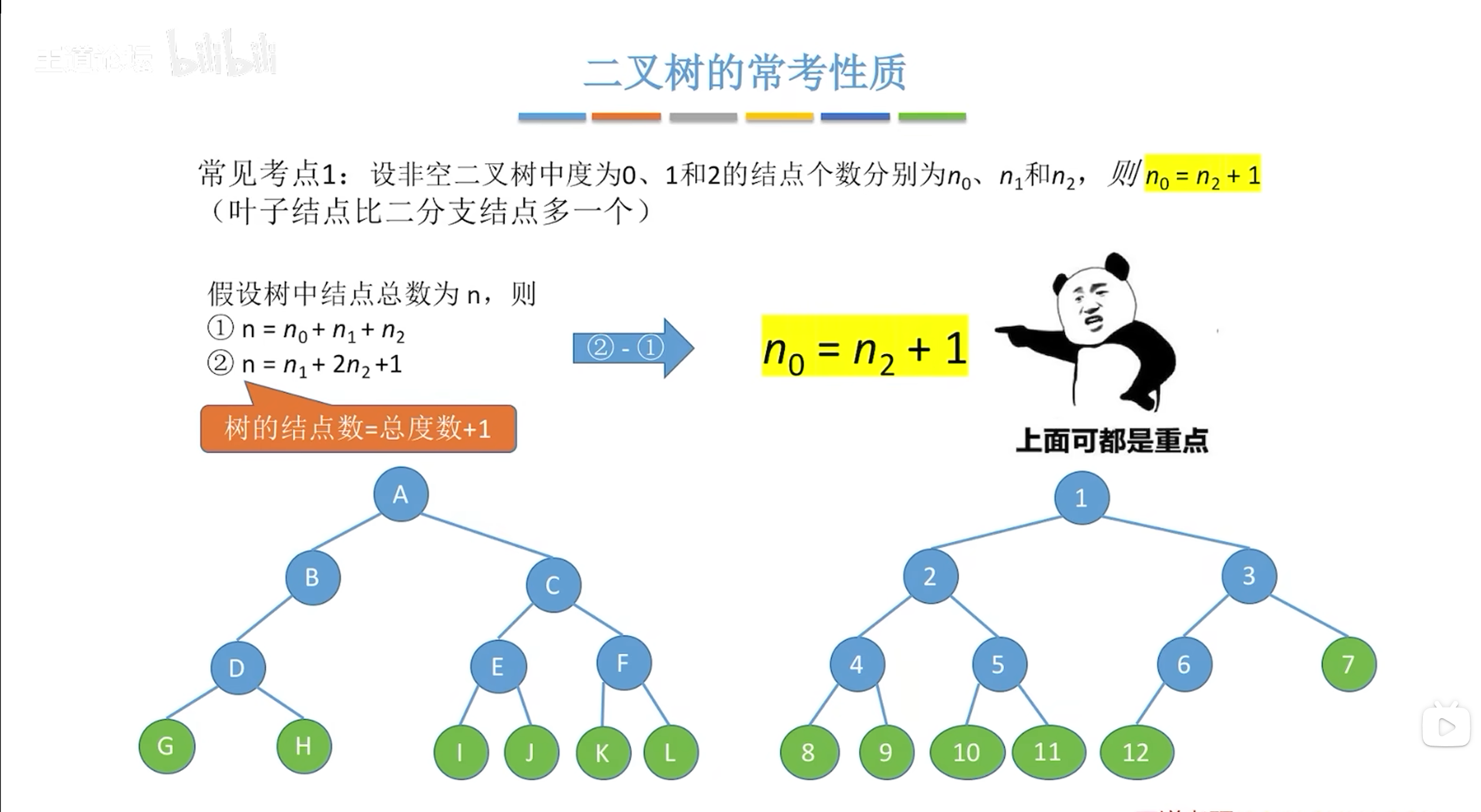
叶子节点的个数要比度为2的节点个数多一个;
n=n1+2n2+1:度为1的节点提供1个分支,度为2的节点提供2个分支,没人给根节点提供分支所以+1;
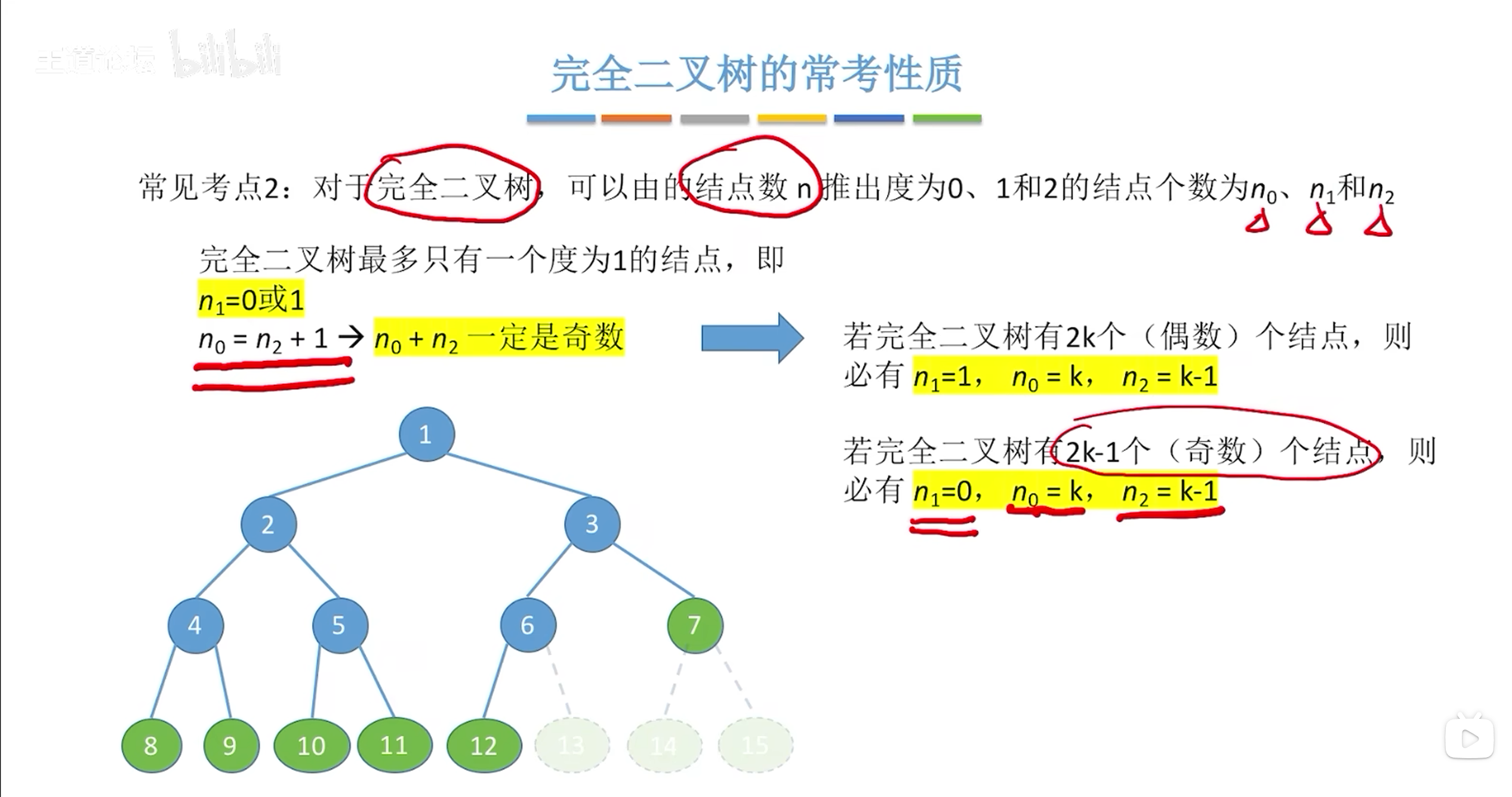
相邻数相加为奇,同时n1为0或1,
已知二叉树的结点个数为奇数或偶数时可以确定n1的个数
奇:n1=0;n0+n2=2k;n0=n2+1;联立得到个数
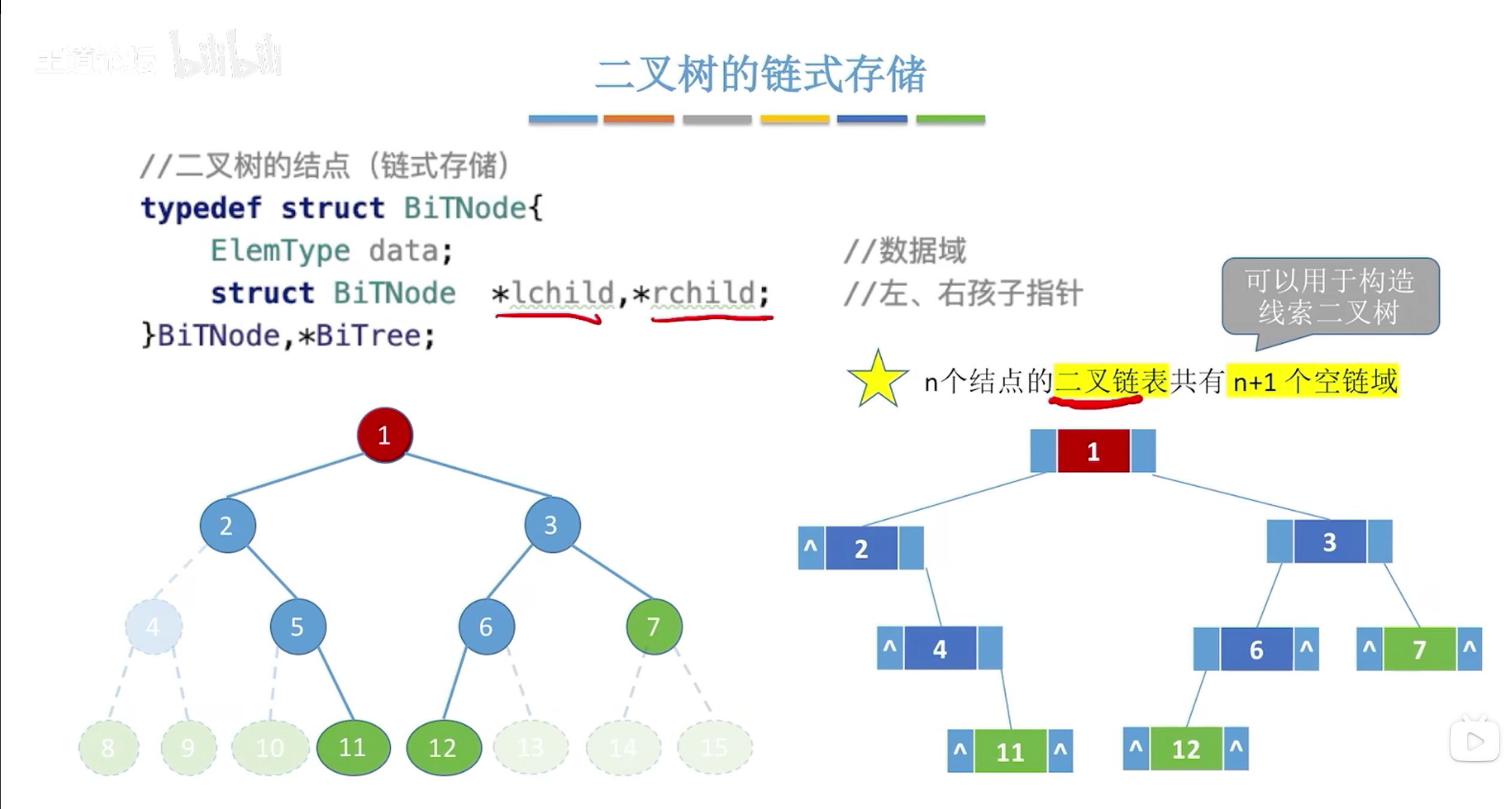
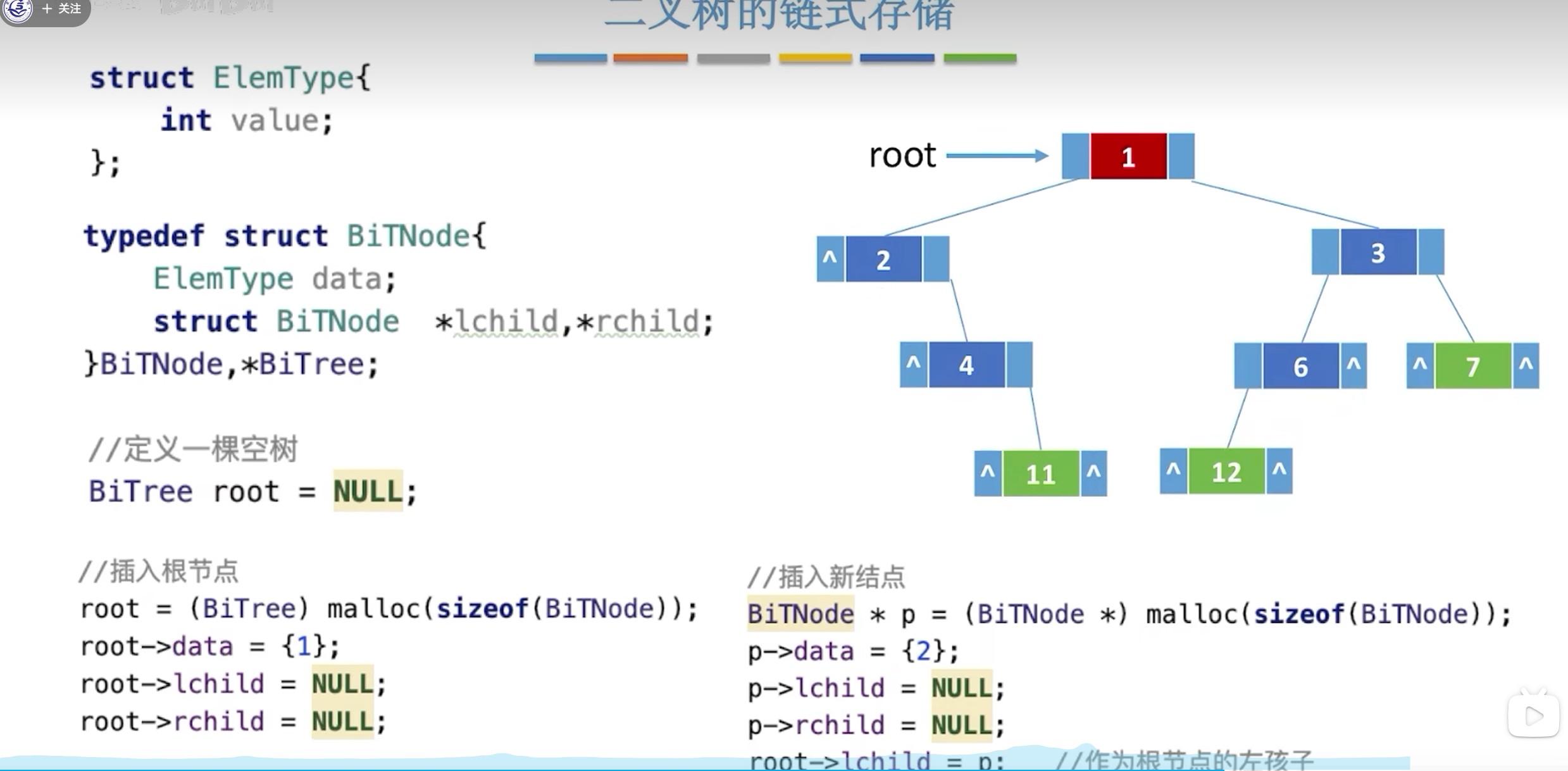
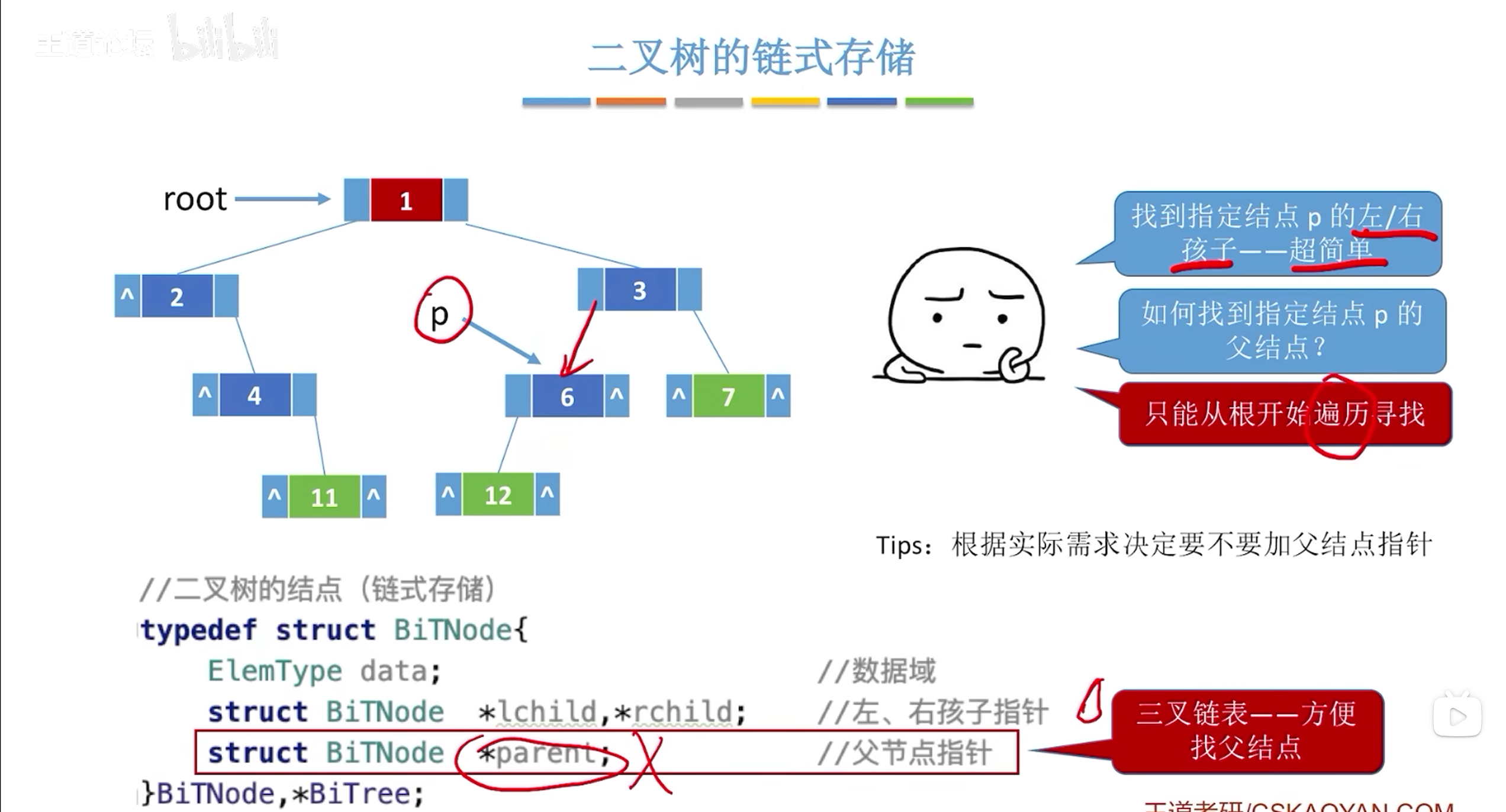
二叉树的存储结构
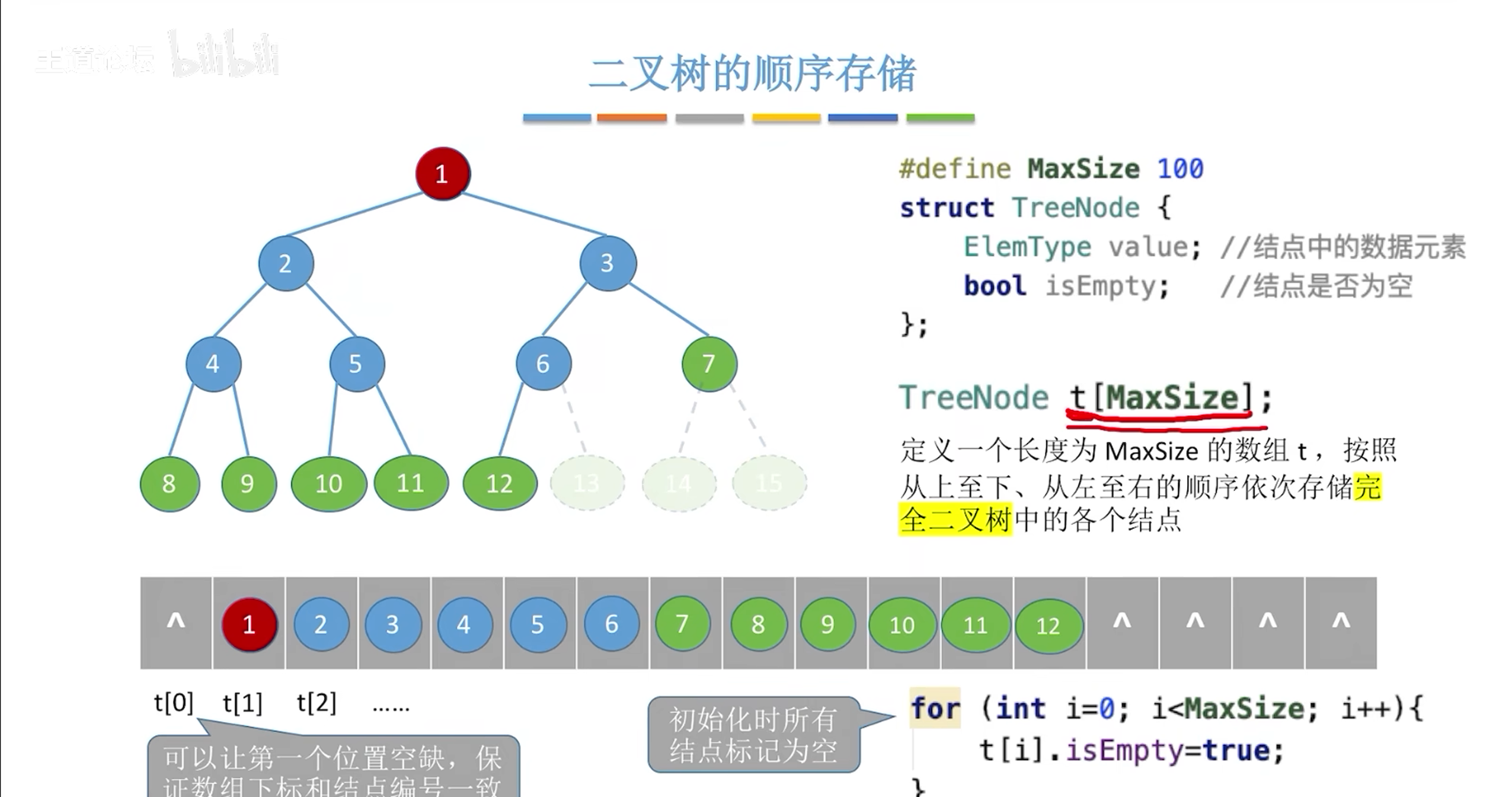
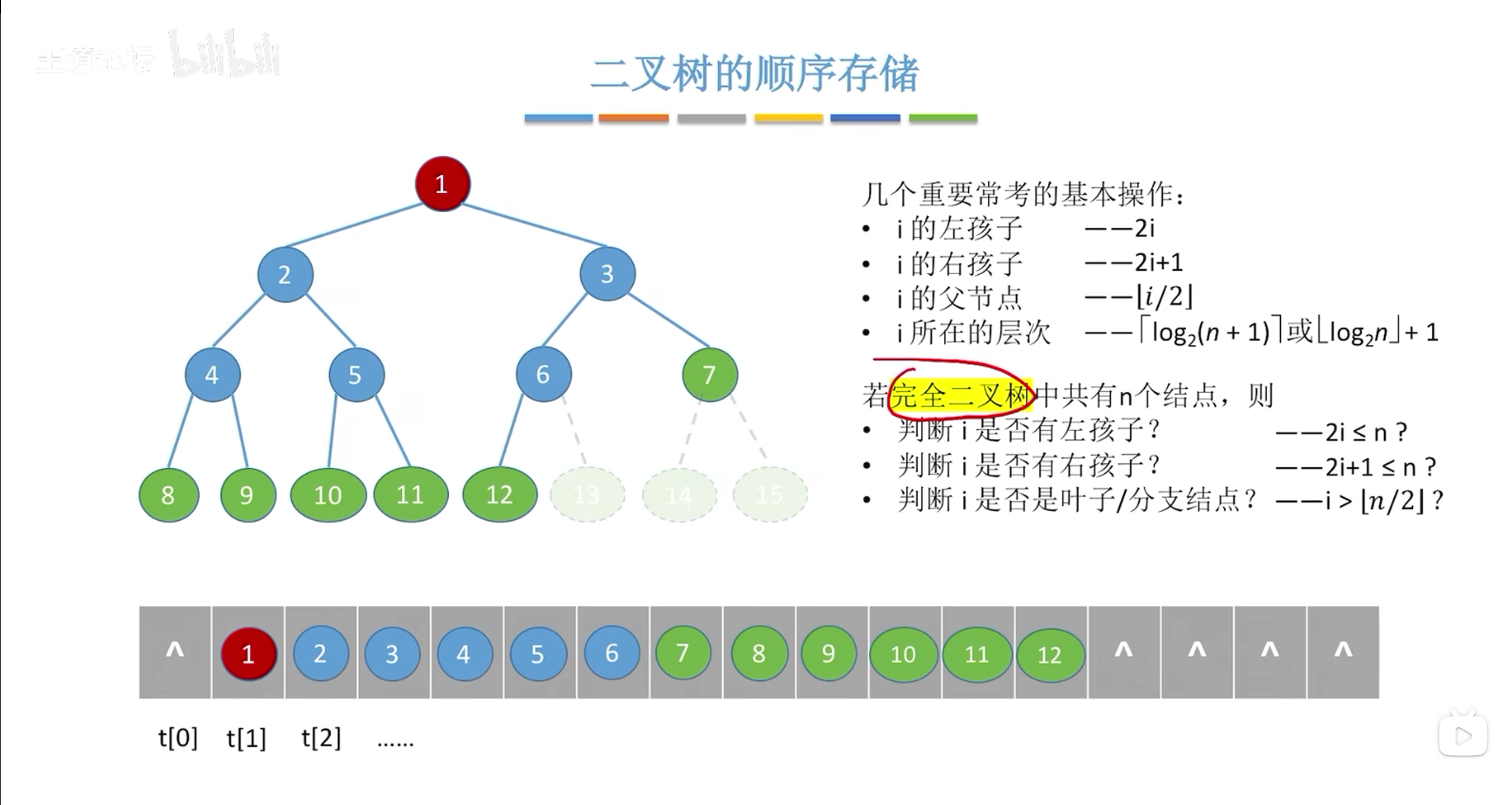
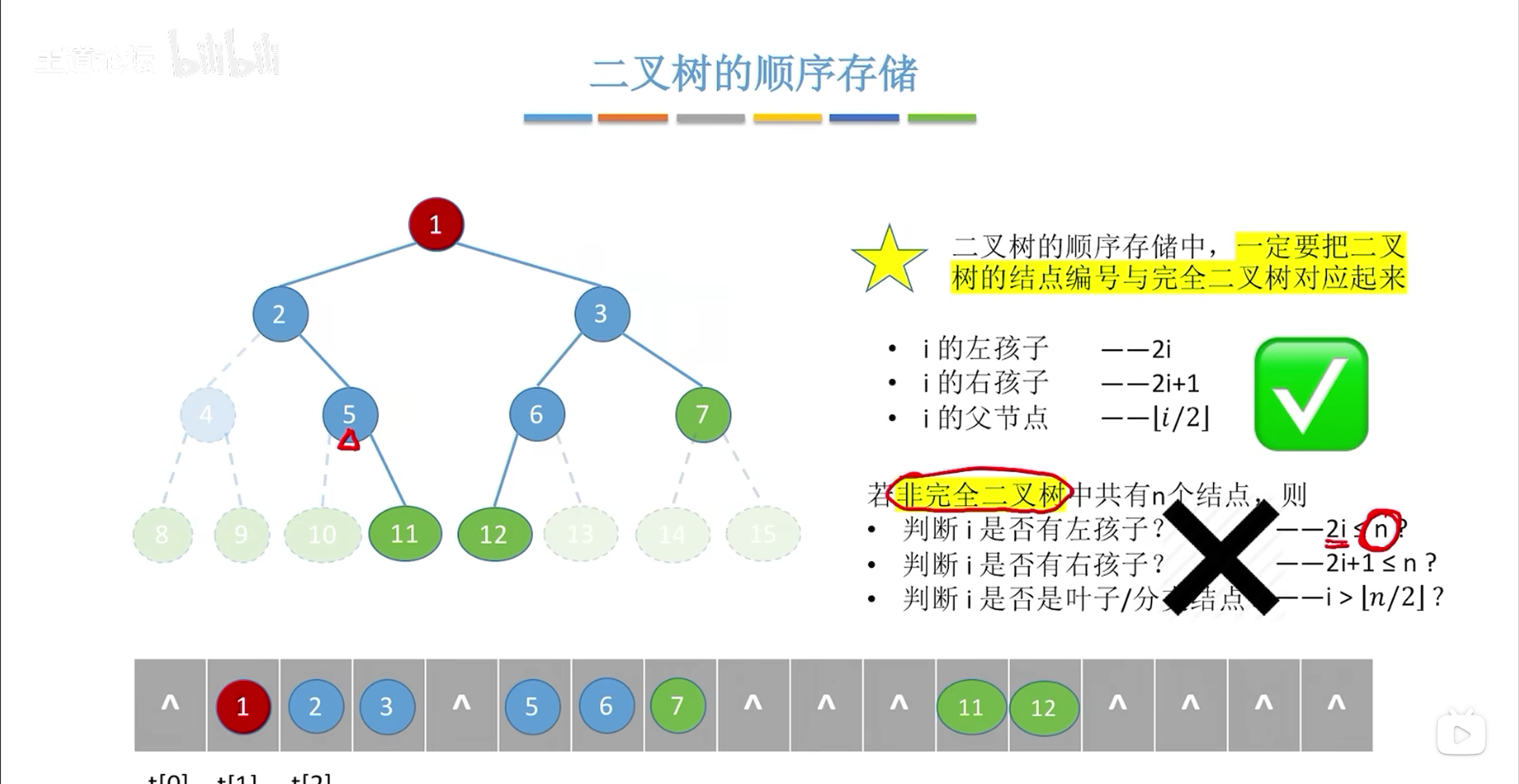
非完全二叉树可以通过跳跃存储的方式反应他们的逻辑关系
通过2i 2i+1找到节点的左孩子和右孩子访问第二个数据判断是否存在true
这种存储方式存在空间浪费
最坏形式
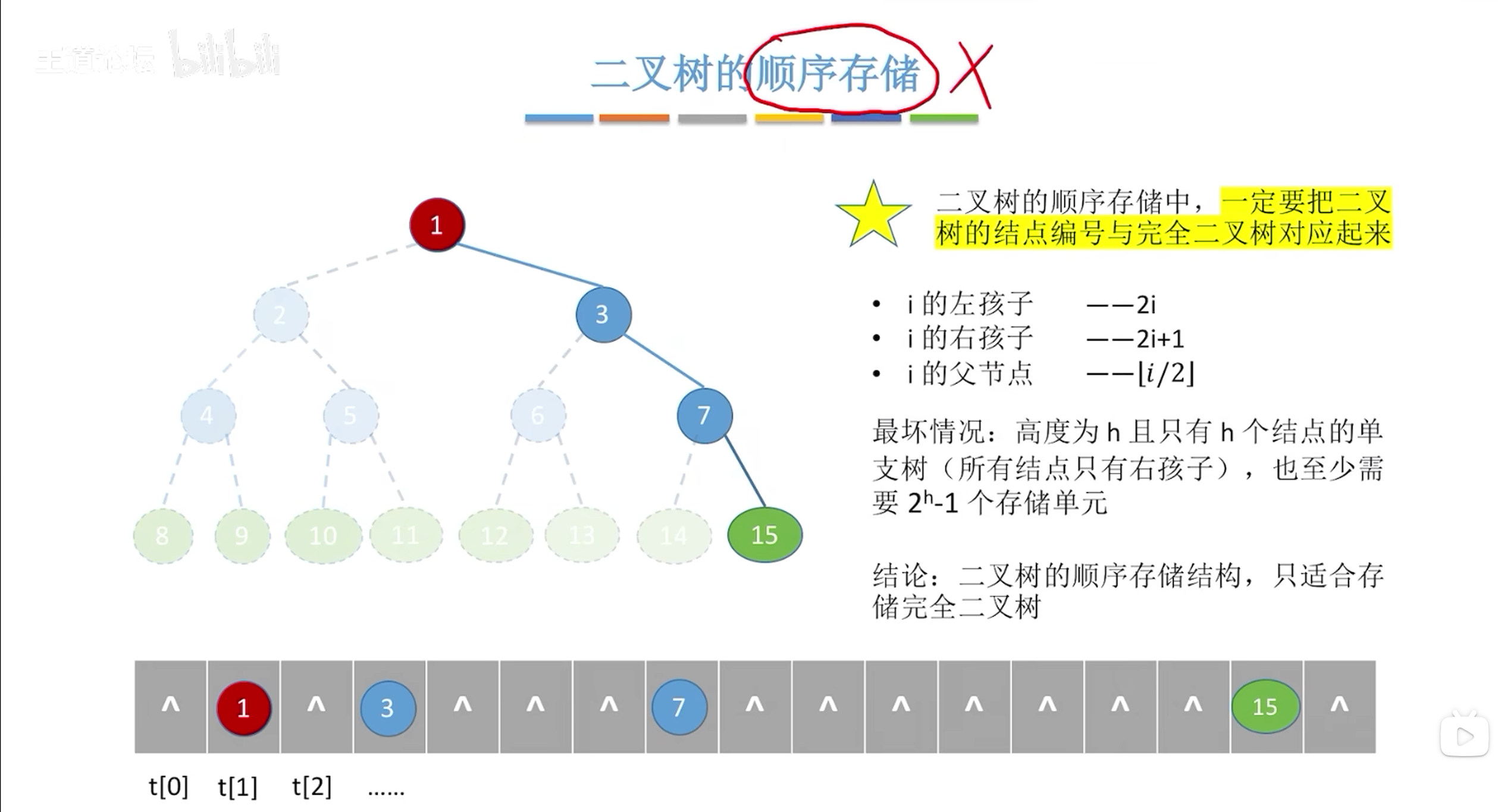
实际应用当中很少用顺序存储二叉树