简单几何问题的通解
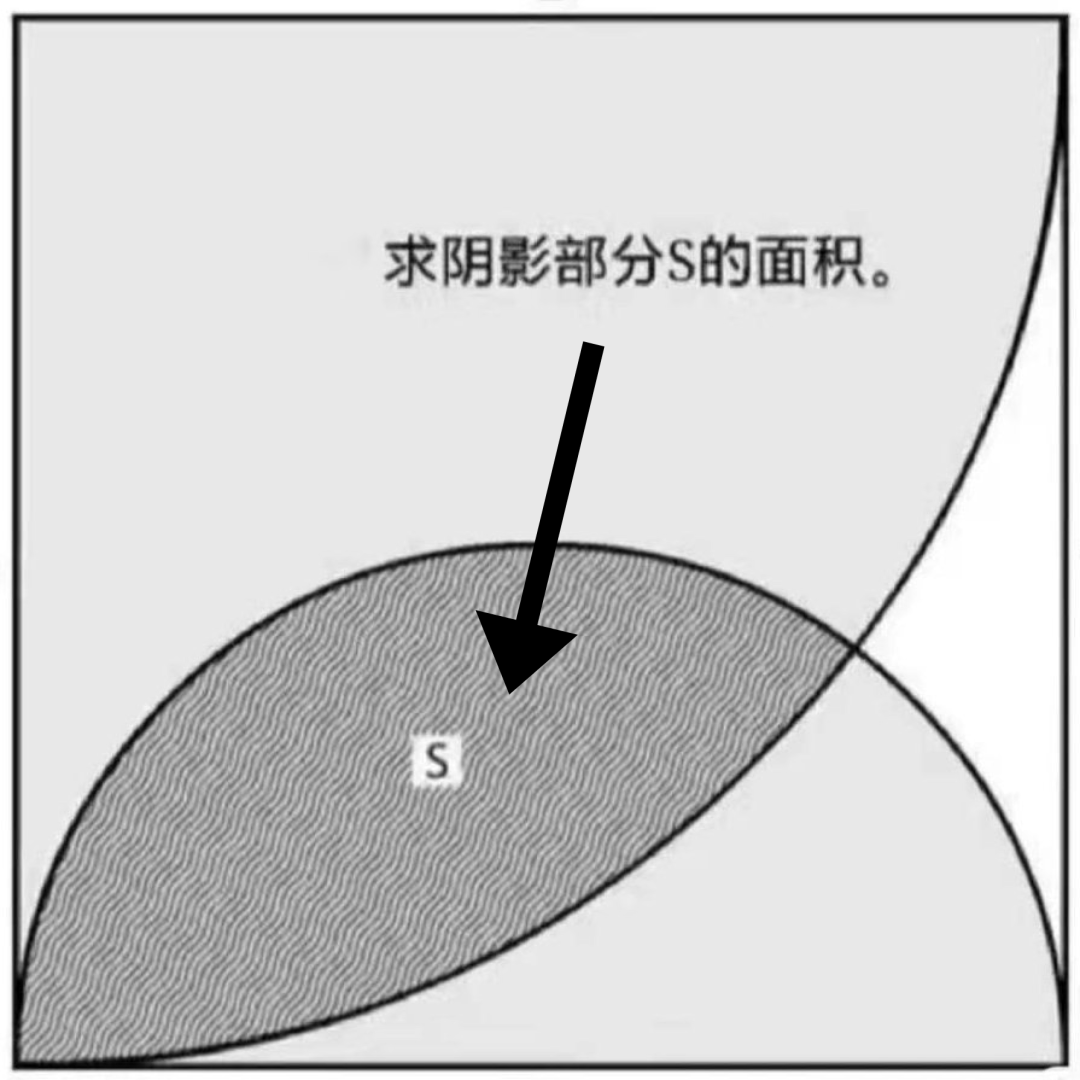
来,这道题怎么做?边长为2的正方形内,2个扇形的交集面积是多少?这道题一定要画辅助线,因为要用到两个扇形的交点,如果不画辅助线,这个交点相关的4个子图一个都无法求出面积,只能求出子图的组合面积,但组合面积又和交点无关了。连接交点和2个圆心。
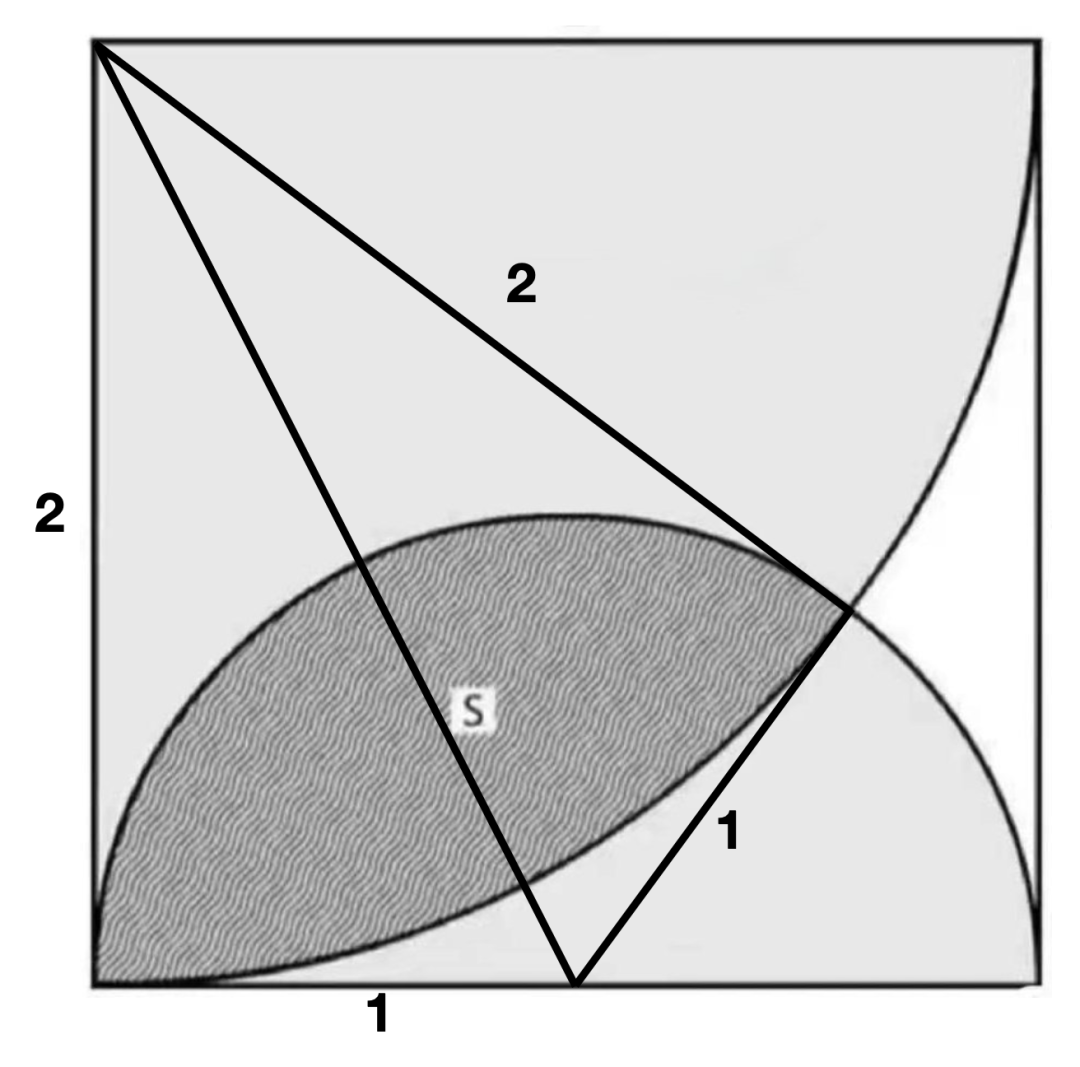
这一下子不就明了了嘛,这2个直角三角形全等,面积之和(纸飞机形)为2。要求阴影面积只要把2个扇形面积相加再减去2就好了,就是4*Math.atan(.5)+Math.atan(2)-2=0.961739153797315≈1。
数学题的复杂度根本上就等于题目难度,如果遇到这种【看似很简单】实际上一时半会想不到结果的数学题,或者是列了很长一个式子花了很长时间才解出来,那一定是你掌握的基本方法欠缺了某些,如果掌握了所有的基本公式,那么就不存在什么【看似简单实则困难】的题目了。比如这道题首先要知道辅助线怎么画,然后快速地决定用【二元容斥】来解阴影面积,然后看到扇心角可求,立刻用弧*径/2得到扇形面积,最后2个扇形之和减去2个全等三角形=S。从始至终的每一步都采用了最简便的算法,最后列出的式子也很简单。这种基础训练每个人都应该掌握。
