锥线性规划【分布鲁棒、两阶段鲁棒方向知识点】
1 锥线性对偶理论
本部分看似和分布鲁棒、两阶段鲁棒优化没什么关系,但值得优先学习,原因将在最后揭晓。
- 二阶锥
二阶锥(second-order cone,又称ice-cream/Lorentz cone)的形式为:

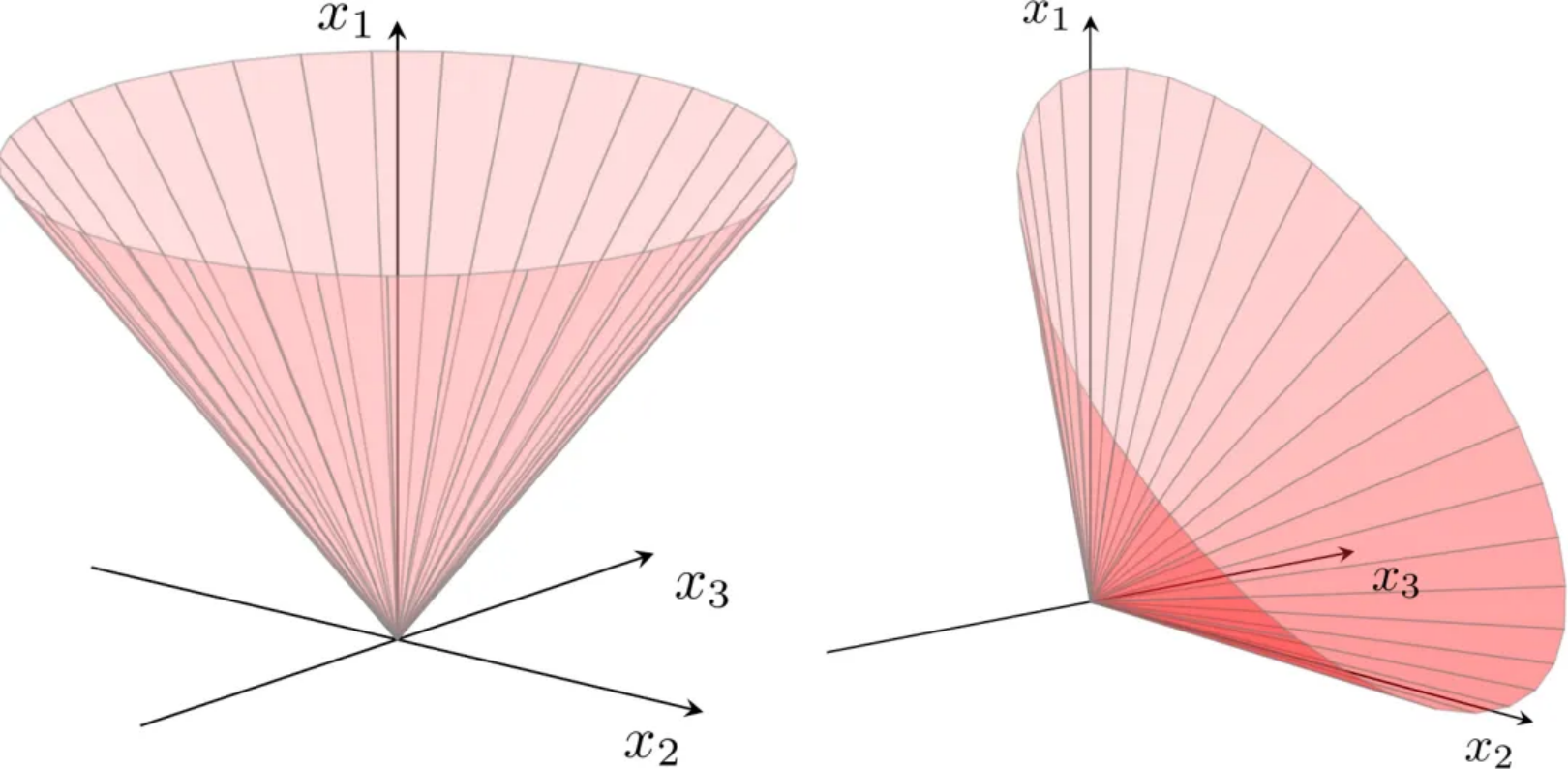
- 非负象限锥

- 半正定锥

- 锥线性规划与线性规划的关系
为什么说锥线性规划是线性规划的拓展呢?回顾线性规划标准型:


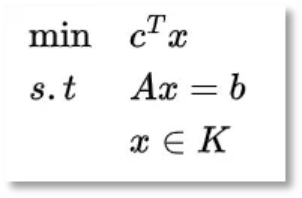

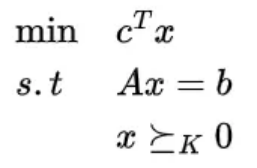

- 对偶锥
锥K的对偶锥定义为:

- 锥线性规划的对偶问题
- 为了更加具有一般性,以后目标函数就用内积的形式写了。考虑原问题:
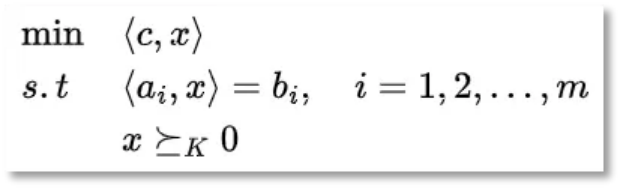

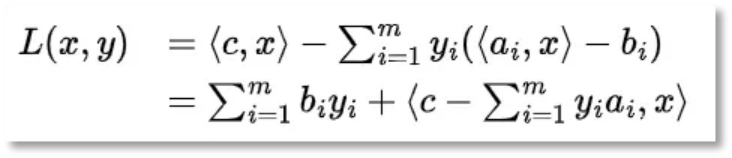
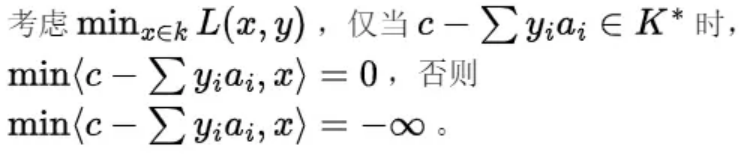
其中:
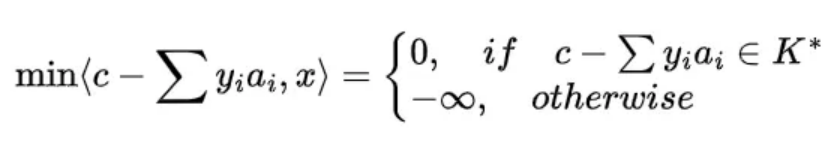
因此,原问题的对偶问题为:
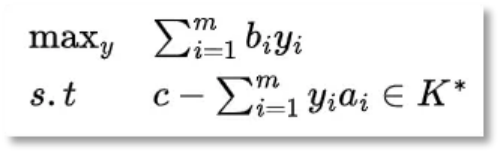
可以看出,锥线性规划对偶问题的推导也与线性规划对偶问题的推导十分相似。
- 强对偶性的成立条件
若原问题或对偶问题有界且存在严格可行解,则强对偶性成立。(与线性规划强对偶性的成立条件相比,多了一个“严格可行”)

须注意:在锥线性规划中,若的原问题有界且存在严格可行解,则对偶问题有最优解;若对偶问题有界且存在严格可行解,则原问题有最优解。而在线性规划中,只要原问题或对偶问题有界且存在可行解,则原问题和对偶问题都有最优解。
2 锥线性对偶应用
- 分布鲁棒应用
回顾鲁棒线性约束:
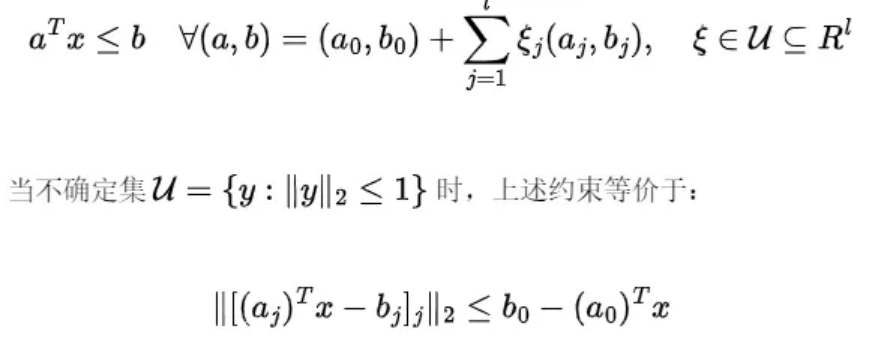
其实,它就是一个二阶锥约束!这也就是要在进一步学习分布鲁棒优化之前先学习锥线性规划的原因。我们费劲心思把一个优化写成线性规划、二阶锥规划或半正定规划问题,是因为它们都是比较“标准”的凸优化问题,求解方法非常成熟。
- 两阶段鲁棒方面
我们都知道配电网模型的一大特点就是二阶锥模型,在配电网两阶段鲁棒优化过程中需要对二阶锥进行对偶,本质上用到了本次分享的内容,具体锥对偶方式可以详见视频讲解内容:
视频讲解|配电网两阶段鲁棒优化模型(以33节点为例)
