牛顿迭代多维+原理推导

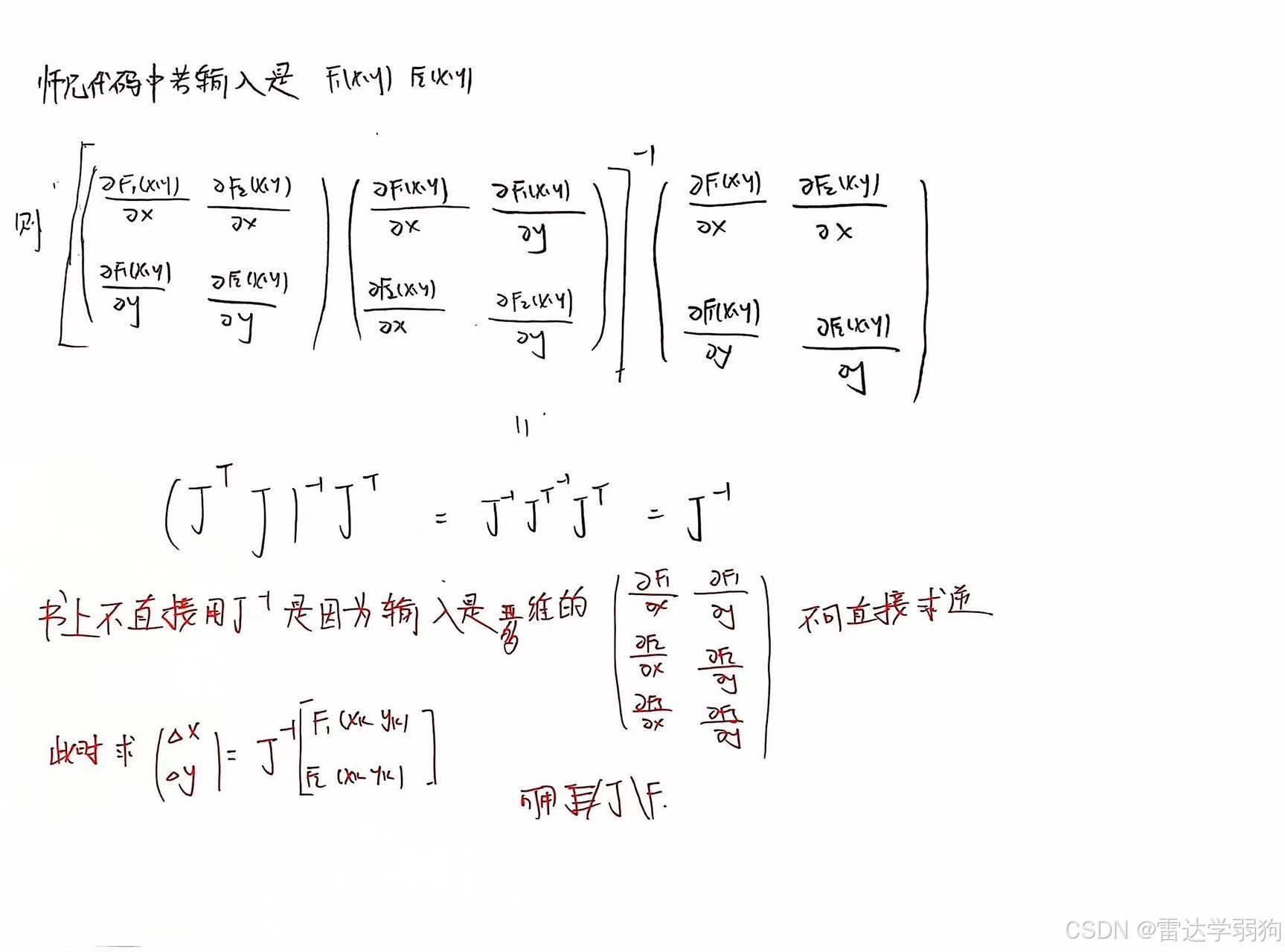
这是两个函数了两个变量的情况，对于三个函数两个变量，牛顿迭代的雅可比矩阵不能求逆，

右边的增量的求解就不能用这个公式了呢。对于有逆矩阵但不能求逆的公式，这个逆矩阵是求解线性方程时出现的，就可用不求逆的方法解线性方程

牛顿迭代原理推导：两个函数，两个未知数为例的泰勒展开

矩阵的逆出现，其实就是求解方程组时出现的，所以矩阵不可逆的时候，可以直接用求解线性方程组的方法，求解出结果。三个方程两个未知量，有唯一解。

下面这种泰勒展开是一个函数两个未知数的二阶泰勒展开，后面的那一项是海森矩阵                                                      

、

多个函数的泰勒展开，其实就是这种单个函数泰勒展开的简单拼接而已