每日一练2627——变态跳台阶快到碗里来不用加减乘除做加法三角形
文章目录
- 变态跳台阶
- 思路:
- 代码:
- 快到碗里来
- 思路:
- 代码:
- 不用加减乘除做加法
- 思路:
- 代码:
- 三角形
- 思路:
- 代码:
变态跳台阶
题目链接:
思路:
这个题目很容易理解,但公式推导有些麻烦
假定第一次跳的是1阶,那么剩下的是n-1个台阶,跳法是f(n-1);
假定第一次跳的是2阶,那么剩下的是n-2个台阶,跳法是f(n-2);
假定第一次跳的是3阶,那么剩下的是n-3个台阶,跳法是f(n-3)
…
假定第一次跳的是n-1阶,那么剩下的是1个台阶,跳法是f(1);
假定第一次跳的是n阶,那么剩下的是0个台阶,跳法是1种(f(0)==1);
根据题图解析可以得出
有一阶台阶的时候 f(1) = f(0) =1;
有两阶台阶的时候可以有 f(2) = f(1)+f(0)=2;
有三阶台阶的时候可以有 f(3) = f(2)+f(1)+f(0)=4;
…
有n阶台阶的时候,总跳法为:
f(n-1) = f(n-2) + f(n-3)+.... + f(1) + f(0)----------------1
f(n) = f(n-1) + f(n-2)+.... + f(1) + f(0)-------------------2
用2式减去1式可得,f(n)=2*f(n-1)
代码:
class Solution {public:int jumpFloorII(int number) {if (number == 1) //当有一阶台阶的时候{return 1;}return 2 * jumpFloorII(number - 1);//当有n阶台阶的时候}
};
快到碗里来
题目链接:
思路:
这个题目很容易理解,只要输入的猫的身长小于碗的周长即可,通过输入碗半径计算得到周长,与输入的猫的身长相比较。
但是!
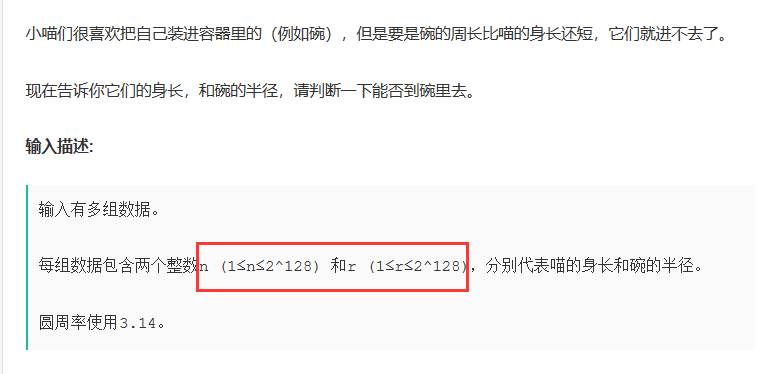
注意看数据范围,这里的数据范围远超整形,使用double才能装下这么大的数据。
代码:
#include <iostream>
using namespace std;
int main() {double n, r;while (cin >> n >> r) {if (n > (2 * r * 3.14))cout << "No" << endl;elsecout << "Yes" << endl;}return 0;
}
不用加减乘除做加法
题目链接:
思路:
不使用+运算符进行加法运算
数字的相加可以转换为二进制的加法,注意每一位相加与进位即可
- 两个数异或:相当于每一位相加,而不考虑进位;得到相加后不包含进位的数据
- 两个数相与然后再左移一位:得到两数相加的进位
- 如果进位不为0,两个结果按章按照上面的方式相加,直到进位为0,得到正确的结果
代码:
class Solution {public:int Add(int num1, int num2) {int digit = num1 ^ num2;int carry = (num1 & num2) << 1;while (carry) {int tmpdigit = digit;digit = tmpdigit ^ carry;carry = (tmpdigit & carry) << 1;}return digit;}
};
三角形
题目链接:
思路:
需要了解三角形的组成条件:最小的两边相加大于第三边即可,对输入的三个数字进行排序,最小的两个相加与另一个数进行比较。
需要注意的是定义变量的时候要用double
代码:
#include<iostream>
#include<algorithm>
using namespace std;
int main() {double index[3];while (cin >> index[0] >> index[1] >> index[2]) {sort(index, index + 3);if (index[0] + index[1] > index[2]) {cout << "Yes" << endl;} else {cout << "No" << endl;}}return 0;
}
end
