当前位置：首页 > news >正文

阿哈罗诺夫——玻姆效应（AB效应）

news 2025/7/29 4:27:42

规范变换

$\nabla \times (\nabla \times A)=\nabla(\nabla\cdot A)-\nabla^2A$

规范场是与物理规律的定域规范变换不变性相联系的物质场

$\oint A\,dl=\iint\nabla \times A\,dS$

$\nabla \times E=-\frac{\partial B}{\partial t}=-\frac{\partial (\nabla \times A)}{\partial t}=-\nabla\times \frac{\partial A}{\partial t}\Rightarrow \nabla\times(E+\frac{\partial A}{\partial t})=0$

纵场的旋度为零,横场的散度为零

$E+\frac{\partial A}{\partial t}=-\nabla \phi$

由于 $\nabla\times(\nabla g)=0$

因此 $B=\nabla\times A=\nabla\times(A+\nabla g)$

为了消除此影响，我们需要对标势场做规范
- 库伦规范(Coulomb gauge):使麦克斯韦方程组自然满足静电场的条件

$\nabla \cdot A=0$

- 洛伦兹规范（Lorentz gauge）:满足洛伦兹变换不变性

$\nabla \cdot A=-\frac{1}{c^2}\frac{\partial \phi}{\partial t}$

带电粒子在磁场中的总动量

电磁场的动量

$\vec{G_{e,m}}=\int_V\varepsilon _0(\vec{E}\times \vec{B})d\tau'= \int_V\varepsilon _0(\vec{E}\times (\nabla\times A))d\tau'$

稳定条件下， $\nabla\times E=0,\nabla\cdot A=0$

得到 $\vec{E}\times(\nabla\times A)=\nabla(\vec{A}\cdot \vec{E})-\nabla\cdot (\vec{A}\vec{E}+\vec{E}\vec{A})+\vec{A}(\nabla\cdot \vec{E})$

$\vec{G_{e,m}}=\varepsilon _{0}\left [ \int_V \vec{A}(\nabla \cdot\vec{E})d\tau' +\oint_S(\vec{A}\cdot\vec{E})dS' -\oint_S(\vec{A}\vec{E}+\vec{E}\vec{A})\cdot dS' \right ]=q\vec{A}$

因此，带电的运动粒子在外磁场中的总动量

$\vec{p}=m\vec{v}+q\vec{A}$

AB效应

量子力学中，电势与磁标势具有可观测的物理量的效应

AB实验装置

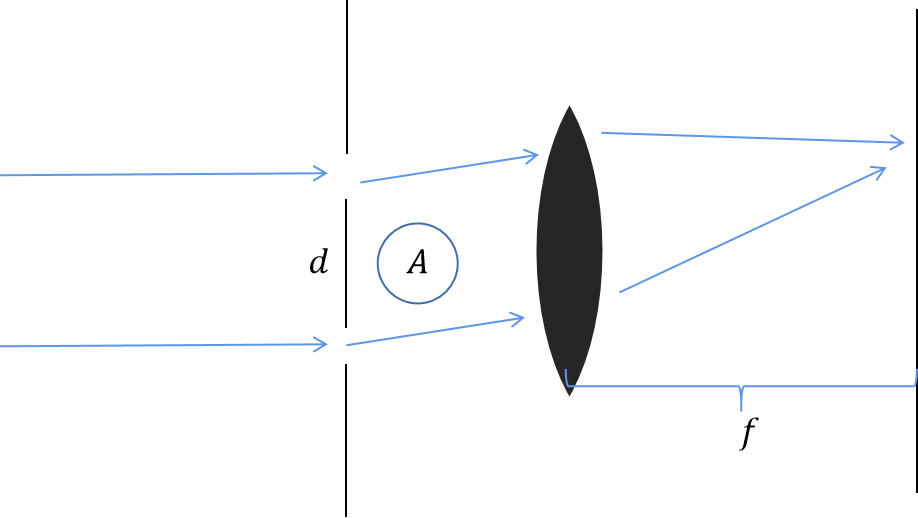
螺线管不通电时，电子波函数的相位是

$\phi = \int \vec{p}\cdot d\vec{r}$

通过两狭缝的电子波函数相位差

$\phi_1-\phi_2=kdsin\theta$

屏上暗纹的位置是

$y=f\,tan\theta\approx \frac{(2n+1)\pi}{k}\frac{f}{d}$

与电子速度共轭的正则动量为

$\vec{p}=m\vec{v}-e\vec{A}$

接通螺线管后

$\phi_1-\phi_2=kdsin\,\theta+\int_{c_1}-\frac{e\vec{A}}{\hbar}\cdot d \vec{r}-\int_{c_2}-\frac{e\vec{A}}{\hbar}\cdot d \vec{r}=kdsin\,\theta-\frac{e}{\hbar}\Phi$